After taking last week off, Problem of the Week makes a triumphant return. Problem Five is now ready for your consideration.
The main problem for this week, in keeping with the arithmetic theme for this semester, is an especially famous “alphametic” problem. If you like that sort of thing, then you might enjoy perusing this website.
As a bonus problem, however, I also presented a second classic brainteaser. And here it is:
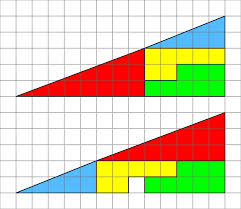
Isn't that weird? Some area seems to have been lost in rearranging the pieces of the first triangle to get the second. This is one of those puzzles that still seems incredible even after you know the explanation. What is going on?
Feel free to has that out in the comments.
More like this
Are you practicing the "no problem" hand? You know how it goes--"there's no problem" (damn persnickety do gooders)! And even if people sometimes think that there is a problem, the problem that isn't a problem is caused by bad apples. But it really isn't even a problem.
Now that we've gone through a very basic introduction to computational complexity, we're ready
to take a high-level glimpse at some of the more interesting things that arise from it. The one
that you'll hear about most often is "P vs NP", which is what I'm going to write about today.
The link below will take you to a short movie (
Okay, you've tried denying that the problem exists, you've tried to trivialize the problem, and you've even argued that the problem causes so harm, so it isn't a problem. Obviously, this no harm thing begins to have diminishing returns. What's next?

Neither of them is a triangle. The red triangle is 3x8 for a slope of .375, while the blue one 2x5 for a slope of .4 -- by eye they look similar, but the discrepancy means the top shape is concave while the bottom is convex, meaning the bottom has more area total by one unit. The remaining rectangle is 3x5=15 in the top while in the bottom is 2x8=16.
I'd say that's not a true triangle. The hypotenuse of the complete triangle should be sqrt(5^2 + 13^2) = sqrt(194) long. The length of the hypotenuse of the red triangle is sqrt(3^2 + 8^2) = sqrt(73) and the length of the hypotenuse of the blue triangle is sqrt(2^2 + 5^2) = sqrt(29), but sqrt(73) + sqrt(29) is not sqrt(194).
To expand on the earlier two comments, the slope of the blue hypotenuse is about 22 degrees, while the slope of the red one is closer to 20.5 degrees. So not a true triangle.
The SEND MORE MONEY problem is fun, too. Here's how to reason through it.
1. Two four-digit numbers never add to more than 19998, so M has to be 1.
2. We'll be summing SEND with 1ORE. To break five digits, S has to be 8 or 9, which means O has to be 0 or 1. Since M is already one, then O is 0.
3. We have SEND + 10RE = 10NEY. Noticing that we have a 0 in the 100s place of 10RE, and that the E from SEND does not pass to the 100s place of 10NEY, we can reason that ND+RE > 100 -- the 1 carries, so E+1=N.
4. S is either 8 or 9. If S is 8, then we have 8END+10RE=10NEY, so E has to be 8 or greater (87ND+10RE 10 (the 1 carries).
6. We have 9END+108E=10NEY. Unused numbers are 234567. Since Y can't be 0 or 1, D+E must actually be 12 or greater. This must either be 7+5 or 7+6. E can't be 7 because N is E+1 and we've already used 8, so D=7. Then E can't be 6 either, because N would have to be 7 and D is already 7. So E is 5, which makes N=6, and Y=2.
Final result:
9567+1085=10652
O=0
M=1
Y=2
E=5
N=6
D=7
R=8
S=9
Normally I wait a week before publishing my solution, but I guess it's already been spoiled now. :)
My reasoning was similar but not identical to Another Matt; my reasoning was also a bit more convoluted. Here goes:
1. S + M cannot be more than 18. The carry is either 0 or 1, and they have to be different digits, so the maximum result is if one is 8 and the other 9 with a carry of 1. Thus, we can instantly see that M = 1.
2. We can now narrow down S as being either 8 or 9 (since any lesser digit added to 1, even with a carry, would not produce a number that was >= 10).
3. If S = 8, then there is a carry: 8 + 1 + 1 = 10. That makes O = 0. If S = 9, then either 9 + 1 + 1 = 11 or 9 + 1 + 0 = 10 (depending on whether there was a carry), so O is either 0 or 1. But M is 1, so O must be 0 regardless of what S turns out to be.
4. Now that we know O is 0, then we know that the second column from the left must have a carry from the previous column, as otherwise E = N. We know that E cannot be 9, since that would make N 0 (and O is 0). E can also not be 8, since if it was, N would be 9, and we've established that S is either 8 or 9. Thus the maximum E can be is 7, and the maximum N can be is 8. This means that there can be no carry into the leftmost column, meaning that S = 9.
5. So far, we have M = 1, O = 0, S = 9. We can also note that 2 <= E <= 7, and 3 <= N = 12 (as E is the second digit of that result). But if N = 3, then R = 8 (it can't be 9) and there is a carry. This would force D + E to produce a carry; however, in such a case, D could not be higher than 7, and with E = 2 we'd have 7 + 2 = 9 (which not only isn't a carry, it would also force Y = 9 which it can't be). So we conclude that N must be > 3 and thus E > 2.
6. Now we look at the other end of the limit. If N = 8, then E = 7, and N + R + carry = 17. This result is impossible; either there is no carry (so R = 9, and that's already set by S) or there is a carry (so R = 8, but then N = R). So now we know that 3 <= E <= 6 and 4 <= N <= 7.
7. If N = 7 (and hence E = 6), then N + R + carry = 16. We can achieve this only if R = 8 and there is a carry (since R 9). That means that D + 6 produces a carry, and therefore D is either 4 or 5 (since 0, 1, 6, 7, 8, 9 are taken). Neither of these are possible, since they would result in Y = 0 or Y = 1 and Y can be neither of these (M = 1, O = 0). So 3 <= E <= 5 and 4 <= N <= 6.
7. Now we look at N = 6 (and hence E = 5), so that 6 + R + carry = 15. This is a lot more promising. We still need R = 8, and we still need a carry, but now we can set D = 7 and find that 7 + 5 = 12, with Y = 2. This is an entirely valid result, so we can stop here.
So we have 9 5 6 7 + 1 0 8 5 = 1 0 6 5 2, and O = 0, M = 1, Y = 2, E = 5, N = 6, D = 7, R = 8, S = 9.
If we really wanted to, we could continue and prove there are no other possibilities. Continuing above, note that D can ONLY be 7; 0, 1, 5, 6, 8, and 9 are out, and 2-4 + 5 does not produce a carry.
If N = 5 (and hence E = 4), then 5 + R + carry = 14. R = 8, with a carry. is the only way this can work, and that mean that we need D + 4 to produce a carry. In this case, D can be 3, 6, 7. 3 + 4 does not produce a carry, and 6 + 4 = 10 or 7 + 4 = 11 force Y to be 0 or 1, neither of with are possible.
That leaves only N = 4 (and hence E = 3), so that 4 + R + carry = 13. Again, R = 8 and there is a carry, so that D + 3 must produce a carry. D in this case could be 2, 5, 6, 7. Of all these options, only D = 7 produces a carry, and it would force Y = 0, so that's out too.
Thus we can conclude not only that this solution is correct, but also that it is unique.
Ugh, forgive the typos:
In 5, I meant 3 <= N <= 8, not 12.
In 7, I meant that R = 8 and there is a carry (since R cannot be 9).
BTW does this site have math markup capabilities?
At first I couldn't figure it out. But then I noticed that if you look on the left across 5 and up 2, the edge of the blue triangle in the lower diagram, and compare between the two diagrams the point is incrementally higher on the grid in the lower picture that the upper.
If the two larger apparent triangles in the two diagrams were identical they wouldn't show any variation. From there I looked at the slope of the hypotenuse of the red and blue triangles and noted that they differed.
Then I use the side of a pen held up to the two diagrams and noted that there is a visible bow in both the large triangles with the upper diagram being concave and the lower being convex. The difference amounting to the area of one square.
Cool. Nice problem.
One thing I like about the "triangle" problem is that it still seems weird to call the two figures quadrilaterals, which they are. They seem to fit the prototype of "triangle" just enough that calling them "triangles with a bent hypotenuse" seems OK.
PS -- if you let M = 0, which I think goes against the intent of the problem, you can get solutions like:
8542+0915=09457
I think it's generally understood that M has to be greater than zero; it is somewhat unnatural to say that 09457 is a 5 digit number.
Well, that's all the money I got. :)
Of course, the explanations others have given for the triangle problem is correct. It's probably better to describe it as an optical illusion, rather than a brainteaser!
You can solve the triangle problem and understand how it's off by exactly one unit with almost no math. The blue triangle stretches 5 (units) over a 2 rise. To be equal, the red triangle would have to stretch 7.5 units over a 3 rise, rather than the current 8 (5/2*3=7.5 is the only math you need to do here). So it should be a half unit less wide.
Now, look at the second figure and imagine the red triangle is a half unit less wide, with the blue triangle shifted to the right by half a unit. To prevent an overlap, you would then have to chop half of the far right unit square of the yellow shape, and put it on the bottom row...which has been shifted back by half a unit, making the entire area covered perfectly.