The Tricky Thing About Simulated Dynamics

In the previous post about simulating the attraction between sticky tapes using VPython, I ended with a teaser mentioning that there was a discrepancy between the simulation and the theoretical solution from directly solving the equations. The problem is kind of subtle, but clearly visible in this graph from that post:

Data for the toy model version of the system, showing the equilibrium position as a function of initial separation.

In this, we see the equilibrium position that the mass-on-a-spring settles into as a function of the initial separation between the charges in the toy model. For all three masses, there's a very clear tipping point that you can nail down from the shape of this curve, and the maximum value of the equilibrium position is around the same value, 0.26 (that is, 26% of the initial separation-- I'm using scaled variables, here).

So, what's the problem? Well, back when I started this, I set up an equation to describe this system, that has a stable equilibrium point only if the ratio of initial electrostatic force to maximum spring force is 4/27 or less. At a ratio of 4/27, that equilibrium point is 1/3rd of the initial separation. The values I got from my simulation are just a hair over 1/4th of the initial separation. Or, to put it another way, if you calculate that force ratio for the minimum separation for which I could find a stable equilibrium, you get 3.84/27, a little below the maximum allowed by the theoretical model.

So, why the difference? Well, because I was being a little lazy when I set up the simulation. When I coded this up, I released the mass-on-a-spring from the point where the spring is relaxed, which is to say the maximum separation considered in the model. This is a good way to the left of the equilibrium point for the system (that is, the point where the two forces are equal), so the mass shoots over to the right. And, in fact, overshoots the equilibrium point by a bit, before the damping force causes it to settle in to an equilibrium position.

That overshoot is the problem, because the electrostatic force gets bigger as the separation gets smaller, and gets bigger faster than the spring force. Which means that if I put in the parameters to get the maximum allowed ratio of 4/27, the overshoot takes it into a region where the spring can't pull it back.

This is, as I said, a consequence of lazy coding. It came about because I did the pendulum version of this first, and for that system, it's hard to figure out what the equilibrium position ought to be. So I just released things from the easy-to-define maximum separation, and let the system find the equilibrium point for me. When I switched to doing the toy model version, I just used the same basic set-up. But, of course, I have a nice, easy solution for the equilibrium point of the toy model, and can program that in.

As proof that this is the source of the discrepancy, I ran the simulations again, starting the moving mass from a bunch of different release points up to the theoretical value of 1/3rd of the maximum separation, and got the following:

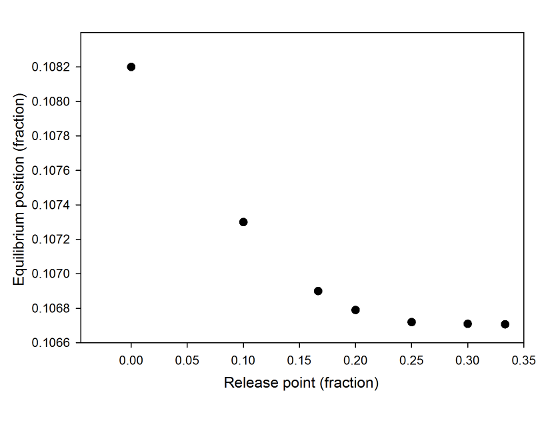The minimum separation as a function of the release position in the toy model of the charged tape system.

You can see that as the release point approaches the theoretical value for the equilibrium position, the minimum separation for which I find a stable equilibrium decreases, settling toward some minimum value. A plot of the measured equilibrium point as a function of this starting point shows an increase toward the predicted value of 1/3rd, though it's not as clearly asymptotic a graph as this one.

For a simulated charge of 20 nC, if I release the mass from exactly the theoretical prediction of 1/3rd the separation between the relaxed position of the spring and the fixed charge, the minimum separation leading to a stable equilibrium is 0.106707 m, and the equilibrium position is 0.3327. That's down into the realm of the numerical errors associated with the simulation. If I use those values to calculate the force ratio, I get 3.99998/27, awfully close to the theoretical prediction.

So, basically, physics works. Hooray! When I'm not lazy about setting up my code, that is.

Another way to approach this would be to bump up the damping force-- I set the drag coefficient more or less at random, and ended up with a value where the system overshoots and oscillates a couple of times before settling down. If I made the drag force bigger, I could reduce the overshoot, or even eliminate it. That's another rich area of dynamics that I could play around with, if I find myself in need of cat-vacuuming.

The other thing to do with this would be to take the same approach to the pendulum model. I still don't know the right theoretical value for the release point there, but the universality of the models that we saw in the previous post probably comes to my rescue, there. That is, the equilibrium points I was seeing for the pendulum fall on the same curve as the mass-on-a-spring toy model, so I could probably just set it up to start with the same separation, and go from there. It's a little more annoying to code, though, so I haven't bothered, yet.

Anyway, that's the latest refinement of the sticky tape saga. I have one more thing to look at, but I'll save that for a final post, tomorrow.