Relativity and Baseball

It's baseball playoff time, so sport shows are full of one of the great mysteries of the season, exemplified by this .gif (from SBNation):

Raul Ibanez hitting a game-winning home run. GIF from SBNation.

No, not "Raul Ibanez, really?" but "How can he make the ball go that far?" After all, even very good outfielders are lucky to reach home plate with a throw from the warning track. Not even the hardest-throwing pitcher could stand at home plate and throw the ball into the second deck of a baseball stadium. Yet it's not uncommon for the ball to end up there after being hit by a bat. So, how does that work?

It turns out, you can understand this using relativity.

No, I don't mean hitting a pitch moving at relativstic speed, which would be ridiculous. I'm talking about an older form of relativity, dating all the way back to Galileo Galilei, king of night vision the great Italian proto-physicist and science popularizer.

Galileo gets credit for introducing the idea that relative motion is the only thing that matters (though he may have gotten it from some less famous predecessor; I'm sure Thony C. will leave a comment if that's the case), most famously in the Dialogue, where it's part of demolishing the argument that if the Earth was really going around the Sun, we'd feel the motion. In fact, as he argued using a thought experiment on a ship, you don't see any difference in the way physics works whether you're moving or standing still.

Galileo initially deployed this for propaganda purposes, but it's an extremely powerful idea, and the direct precursor of Einstein's famous theory. It's also the key to solving a lot of really difficult physics problems. Like, for example, the problem of hitting a baseball vastly farther than you can throw it.

If you look in detail at the interaction of the ball and bat, it's kind of an awful problem. Both of them are moving rapidly, and during the time they're in contact, the ball deforms significantly, as you can occasionally see in super-slow-motion footage:

A baseball deforming as it hits the bat of Miguel Cabrera, from NESN.

(Contrary to the framing of the article, this isn't a testament to the unique prowess of Miguel Cabrera, though he is a hell of a player. Pretty much anybody who hits a baseball squashes it during the short time the ball and bat are in contact; you just need to be kind of lucky to get a clear image of it.)

There are two things you can do to make the problem a lot easier. One is just to invoke the idea of momentum, a physical quantity associated with systems of moving objects that does not change due to interactions within the system. If you know the mass and velocity of the ball and the bat before the collision, you can calculate the total momentum, and after the collision the new velocity of the ball and the new velocity of the bat have to give you the same total momentum. This removes the need to worry about the details of the period when the baseball is squashed, which is good, because those are awful.

The other thing you can do is to invoke relativity a la Galileo. The problem where both bat and ball are moving is still kind of a pain, mathematically, but if one of the two is stationary, then your life gets a whole lot easier. And we know what happens when a light moving object like a baseball hits a heavier object like a bat that isn't moving: the ball bounces back at a fair fraction of the speed it came in at, and the bat only moves a little bit.

So, we can figure out what happens through four steps, illustrated schematically here:

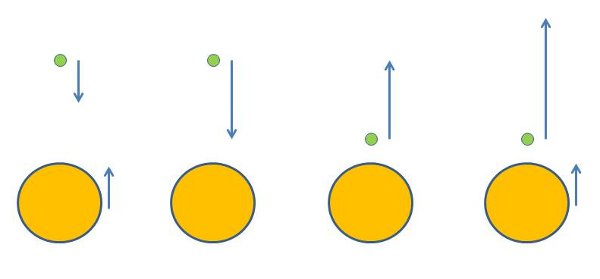Cartoon of two objects colliding. Left, lab frame, before collision. Middle left, heavy object frame before collision. Middle right, heavy object frame after collision. Right, lab frame after collision.

On the left, we have the initial situation: a light object (green) moving in one direction about to collide with a heavy object (orange-ish) moving in the opposite direction. With two moving objects, things are a little messy. But you can make life easier, by switching to the second picture from the left, which is the same situation from the perspective of somebody riding along with the heavy object.

Now you only have one moving object, the light one, and its speed is the sum of the two individual speeds from the original scenario. This makes the total momentum a whole lot easier to calculate.

It also makes it easy to see what happens in the case of a really big mass difference. If the bigger object is heavy enough, it doesn't move at all, and the lighter one bounces back with the same speed that it came in (shown in the third picture from the left). This is, obviously, an idealization, but it lets you get the idea of what's going on. For a real case, the heavy object won't be perfectly still after the collision, but will be moving down at a small and easy to calculate velocity, while the light object will be moving up at slightly less than the speed it came in.

(For something like a bat hitting a ball, there's also the fact that the batter is providing some force to keep the bat from slowing down too much. That makes this a slightly better approximation.)

Now, we know that the light object flies away at the same speed it came in, according to somebody moving with the heavy object. But that's not what we really want-- we really care about what happens in the original frame where both were moving. But that's an easy switch to make: we just undo what we did at the first step of the process, to get to the rightmost picture. This has the heavy object moving up at almost the same speed it came in with, while the light one flies away at a high speed: the speed it came in with, plus twice the speed of the heavy object.

And that's the secret of the upper-deck home run: a baseball leaves the bat moving much faster than it came in. If the bat truly didn't slow down, it would be going at the speed of the pitch plus twice the speed of that bat; those are roughly comparable, so something like three times the speed of the pitch. And if you triple the speed of the ball, you should triple the range; if a good ballplayer can throw the ball from the outfield wall in to home plate, that's around 100m, so the ideal hitter would be able to hit the ball 300m.

In reality, of course, this isn't perfect, so the speed leaving the bat is lower (and we haven't even talked about air resistance on the ball in flight), but this gets you the key idea. And incidentally shows the reason why physicists cared about relativity even before Einstein and E=mc² and all that: changing between frames of reference makes some kind of hairy problems much easier to understand. Like, well, baseball.

------

(This is the same physics behind the soccer ball-tennis ball trick. Bringing relativity into it is something I got from David Mermin's excellent book; I used it in How to Teach Relativity to Your Dog, too.)