I'm trying something new here: I'm going to give you a little bit of information and a teaser, and we'll see -- in the comments section -- whether any of you can figure it out.
Imagine that you went outside, each and every day at the same time, and mapped the position of the Sun. What would you see?
Doing this -- taking a snapshot of the Sun at the same exact time from the same exact place on different days -- gives you what's called an analemma. Now, on Earth, the top of the analemma happens during the Summer Solstice, the lowest point of the analemma happens during the Winter Solstice, and the "crossing" takes place twice a year: once on around April 15th and once (coming soon) about August 31st. Here's an image I found on this site that illustrates what happens throughout the year to the Sun's position:
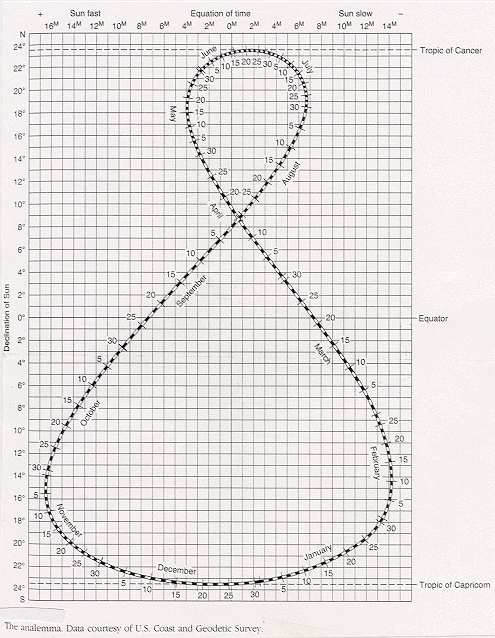
The figure-8 shape that we see happens on some of the other planets, but not on most of them. For example, if we did the same thing on Mars, taking a picture of the Sun at the same exact time every day for a year, we would get a teardrop shape instead of a figure-8:

In fact, if you made a list of what these shapes look like on all the terrestrial planets, here's what you'd find:
- Mercury: a single point (because a day on Mercury takes exactly two years!)
- Venus: an ellipse
- Earth: figure 8
- Mars: teardrop
- Jupiter: ellipse
- Saturn: teardrop with a teeny-tiny loop at the end
- Uranus: figure 8
- Neptune: figure 8
- Pluto: a very large figure 8
So of all the planets close to the Sun, only Earth sees a figure-8. My question for you is this: why does the Sun trace a figure-8 shaped analemma? If you want to go a little beyond that, I'll ask you what the significance of April 15th and August 31st are, too.
Any thoughts?


I'm going to suggest that the figure-8 shape occurs because the Earth's axis isn't fixed relative to Earth's position in space, but wobbles ever so slightly as the Earth rotates.
The significance of the dates? Can't come up with an answer right now.
Because of the tilt of the earth's axis.
The dates are the momenst the earth's axis is perpendicular to the sun-earth line.
Though I really should know this, it's fuzzy in my memory. I would surmise that the sun's lateral movement is due to the elliptical orbit of the Earth, such that our speed differs slightly along our path - this means that at the same time each day, the Earth's rotation (relatively constant) would have the Sun slightly left or right from yesterday, depending on whether you're accelerating negatively or positively.
Then of course, you have the axial tilt which gives the sun its apparent vertical movement.
Combine the left-right and up-down, and you get the analemma. Which can be used to create a rudimentary calendar, obviously, with just a sun dial.
If I'm correct, then April and August must be the apogee or perigee?
The mean sun's Right Ascension changes quicker than its longitude at the solstices and slower at the equinoxes. The RA of the meridian at a particular time changes by a fixed amount each day, hence the side to side wobble twice a year. That, for a circular orbit, gives a symmetric figure 8 with the equinoxes at the crossing point once you take into account the varying declination.
An eccentric orbit means that the actual sun moves quicker than the mean sun at perihelion, and slower at aphelion. The interplay with the symmetric analemma presumably depends on how the line of orbital apses lines up with the equinox, but in general a sufficiently elliptical orbit will force the variations of the actual sun to outweigh the variations in RA for a given axial tilt.
So the answer, broadly, is that Mars is more eccentric than it is tilted, but the other planets (except Mercury, a special case) aren't.
Working out the relevant inequality between e and i is left as an exercise for the blog owner.
Eh? But we know ei Ï - 1 = 0
Axial tilt does not by itself produce the figure 8. If it did, Mars would have a figure 8 analemma as well, since its axial tilt is similar to Earth's. Nor is it eccentricity: Mars has a relatively eccentric orbit, but it only has a teardrop shape. (My guess would be that eccentricity produces an ellipse rather than a circle.)
My best guess is that it has to do with tidal effects, though why those effects would synchronize to the planet's orbital period is beyond me. Earth has the Moon to produce a significant out-of-plane tidal pull, and Charon does the same for Pluto. Elsewhere in the solar system, Jupiter would be the prime suspect, but obviously Jupiter does not exert a tidal pull on itself, and Venus is too far in for Jupiter to have a significant effect. Mars and Saturn feel some effect (which is why they have a teardrop shape), but they are too far in and too big, respectively, to get the full figure 8 effect.
The significance of the crossover dates is a stumper. They are almost but not quite symmetric about the solstice, and they have nothing to do with the line of apsides. It also can't be a question of ascending/descending nodes because both dates are closer to apogee than perigee (it should be the other way around).
I would guess:
Tilted planet + circular orbit = vertical line at noon
(the graph would have the same variation along the "declination" axis, but no variation on the "equation of time")
TIlted planet + elliptical orbit = analemma
(because the angular speed of the earth around the sun changes over the course of the year)
There's other stuff that could be going on from the nutation of the earth's tilt and other similar craziness, but my guess is that those effects are slow.
My guess about the asymmetry of the figure 8 (and why the top and bottom of the figure 8 aren't at the apehelion and perihelion of the orbit, and why the April 15th/August 31st dates aren't symmetric about the apehelion) is due to a misalignment of the earth's tilt and the eccentricity of its orbit?
I can't for the life of me find a way tidal interactions could contribute to the effect. The only tidal interactions to speak of are between the Earth and the Moon.
Though Earth does move around the barycenter slightly, but that's monthly, not annual or semi-annual.
If the Earth's orbit were circular, the sun would take the same path across the sky every day. Axial tilt would make that path rise and lower across the year. The only thing that can change the apparent position of the sun at the same moment each day is if the Earth is rotating slower or faster, or if the combination of the Earth's constant rotation is "adjusted" by the speed of the orbit.
We aren't using sidereal days, so the same time each day is actually not a full rotation, since the Earth has moved during rotation. So I suppose that could account for it, but without any maths, I couldn't say if you'd still need the eccentricity to establish the analemma path.
April 15 and August 31 are when the equation of time are zero with positive slope. Zeros with negative slope would be the solstices.
Break down the problem into parts.
We all know why there are two end points at the solstices. On those days the Sun is northernmost/southernmost and lowest/highest in the sky.
Why are the two end points not connected by a straight line? The orbit of the planet is elliptical.
Why are some planets' end points connected by an ellipse and some connected by a figure eight? We were given an important clue: the graph above shows 4 distinct days during the Earth's year when the Sun is neither fast nor slow. The Earth must be at its average distance from the Sun on those days. What kind of orbit can produce 4 days each year at average distance? Clearly, not a very elongated elliptical orbit because such an orbit can have only 2 days at average distance. So I conclude the Earth's orbit is closer to circular than the other planets that are close to the Sun.
In other words, a circle drawn around the Sun with radius equal to the Earth's average distance from the Sun crosses the Earth's elliptical orbit in 4 places, resulting in a figure eight for the analemma.
This is just a guess, but I feel moderately confident.
With regard to the Earth, I think the explanation is that the length of a day is only on average 24 hours. Around the Summer and Winter solstices it is longer than 24 hours and around the equinoxes it is shorter than 24 hours (this has to do with the Earth's tilt, and the fact that the Earth orbits the Sun; the eccentricity of the Earth's orbit is a negligible factor). The Earth actually once every 23 hours and 56 minutes; the extra 4 minutes is due to the fact that the Earth over a day has moved one degree around its orbit and therefore has to rotate for approximately another 4 minutes to get the Sun into the same position in the sky. (plotting the point where the Sun appears directly overhead on the Earth forms a great circle tilted to the equator, touching the tropics of Cancer and Capricorn, over the year the point where the Sun overhead is, moves about 1 degree, and it is that 1 degree that the Earth has to rotate to give the extra 4 minutes. But at the solstices, the tilted great circle is parallel to the Equator, so one degree crosses more than one degree of longitude ie more than 4 minutes). On June 21 (in the Northern hemisphere), the Sun is at its highest position in the sky. 24 hours earlier, it's about 20 seconds after solar noon so the Sun is slightly lower, and 24 hours later, it's about 20 seconds before solar noon, so again the Sun is again lower (but more to the East). The position on the other planets, I'm quite perplexed; do we have clocks for Martian, Jovian days...
I came back here looking for the answer, but after rereading the above, I take back my earlier comments.
I'm gonna try to work out some simple limiting cases
1) No tilt of axis, circular orbit: sun appears in the same spot every day. The amount of time it takes for one day to pass is determined by the combination of the angular speed of the earth's orbit around the sun and the angular speed of its rotation about its axis.
2) No tilt of axis, eccentric orbit: sun appears at the same "declination" every day, but at a different "equation of time" due to the changing angular speed of the earth's orbit.
3) Tilted axis, circular orbit: You get an ellipse-like thing. The change in "declination" is obvious, but you also get a change in the "equation of time" due to the angle between the axis of rotation and the velocity of the earth. How the orbital angular motion will add with the earth's rotation to determine the length of a day will depend on their relative direction, which changes over the course of an orbit.
Whether or not you get an ellipse, or teardrop, or figure 8 has to do with how the effects of #2 and #3 add together, which presumably changes due to the relative magnitude of the tilt effect and the eccentricity effect, and how they're synchronized.
Mr. Siegel gave us a huge clue in the graph showing "sun fast" and "sun slow" plotted versus date.
Even without having a full understanding, you can see that the Earth's orbit is divided into 4 segments that alternate fast, slow, fast, slow orbital speeds, and this results from the Earth getting closer, farther, closer, farther from the Sun relative to the Earth's average distance from the Sun. The 4 days where the Sun is neither fast nor slow correspond to the Earth's average orbital speed or average distance from the Sun.
The 4 segments in the orbit correspond to the 4 segments in the analemma, each loop of the figure eight has 2 segments, one above and one below the middle. Not all elliptical orbits can have 4 segments. Some can only have 2 segments, one fast and one slow, and the 2-segment orbits are the ones with ellipses.
Mars, looking like a teardrop or half of a figure eight seems to be on the borderline, it's close to having a 4-segment orbit but it just misses.
Pluto, with a very elongated orbit, large distance from Sun, and the Sun near the center, has large figure eight.
It's more difficult for the inner planets to have 4 segments because it doesn't take a large deviation from the circular shape to eliminate 2 of the segments.
I'm doing this mostly by intuition, based on the valuable clue that we got, because we were only asked to explain the difference between ellipse and figure eight, but not required to work out the exact math.
If the Earth's orbit were circular, the tilted axis would make the analemma a line connecting the 2 end points. It's the deviation from circularity that causes deviation above and below the line.
This is a little off topic, but I have been lurking here for a while and figured this would be a good place to ask. What is it that causes elliptical orbits? I have been trying to find out, but haven't yet found anything that explains it very well. Why an elliptical orbit and not a circular, what causes the eccentricity?
I was watching a show on Youtube about space the other day about space and as an example of an orbit a guy put a heavy ball on to a stretched piece of rubber, then rolled a quarter around it. The thing is though, the quarter went in a circular motion without eccentricities, so it got me wondering about why our orbit is like that and why some planets have or less of an eccentricity than earth does. Can anyone help me out with this?
On top of the average vs simultaneous orbital velocity and axial tilt, there is the direction of the axial tilt as well. Think of the consequences of the axial tilt being normal to the direction of motion at perihelion vs being parallel to the direction of motion at perihelion, for example.
After doing some Googling, I have concluded that my answer was completely wrong. Sorry about that. I'm afraid scienceblogs is too advanced for me.
SPOILER ALERT!!!
Graphics- and animation-rich analemma info overload at http://www.analemma.com. Full poop on other planets, or make up your own with Mac & Windows apps.
(The site's been there a while. "Netscape Navigator 4.5 or higher" is required, for instance, and it's 4 years since the last update. WTF? It even calls Pluto a planet!)
Bob O'H @ 5:
You, sir, win one Internet!
Here's my guess. The fact that it's seasonal means it's probably partly due to the tilt of the earths axis. The two planets with the least tilt (Venus: 177.3° and Jupiter: 3.13°) see ellipses. The two planets with tilts most similar to earth (Saturn: 25.33° and Mars: 25.2°) and are giving me some trouble though. Both are tilted slightly more than the Earth(23.44°) but are less figure 8 like. The only other thing I can think of that lines up with seasons is orbital eccentricity. Earth's orbital eccentricity is 0.017 and it makes a figure 8, while Saturn's orbital eccentricity is in the middle at 0.054 and makes a teardrop with a small crossover, and Mars's orbital eccentricity is the highest at 0.093 and it makes a teardrop. So I guess in the end I'm just seconding those who have said tilt and orbital eccentricity. Damn. Just to be different, I'll say that space magic has an effect as well.
We know that for the Earth, the solstices lie close to perihelion/aphelion. Ie the Earth's axis lies close to the plane containing the major-axis of the Earth's orbit, perpendicular to the orbit. My gut tells me that a planet which experiences perihelion/aphelion close to its equinoxes would have a qualitatively different analemma. So I'm guessing that's the explanation - at least until I have some more time to think about it.
The earth is tilted; this gives a nice figure-8 if you're at the equator. Imagine a plane through the earth's equator. The vertical displacement on the analemma is the apparent angle that the sun is below or above the equatorial plane; during the equinoxes the sun is right on the equatorial plane and we're at the node of the figure 8.
Now imagine a plane passing through the earth's axis and through the sun (a longitudinal plane). During the equinoxes, when viewed from the sun, that plane appears to have maximum tilt from a vertical line which is perpendicular to the earth's orbital plane. In other words if I'm on the sun and standing on the plane of the earth's orbit, the longitudinal plane seems to be skewed left or right from the vertical position. As the solstices approach I will see that plane move to an upright position either by twisting clockwise or counterclockwise. From the solstices that line then skews out of the vertical by continuing to rotate in the same direction. The rotation appears to change direction around the equinox. From the earth we see the sun move left and right of the longitudinal plane and cross that plane at the equinoxes and solstices thus producing the figure 8 - unless you're at the poles.
The analemma is not perfectly symmetrical even at the equator and I never learned why or tried to figure it out - would it simply be the ellipticity of the earth's orbit?
I recently calculated myself a sundial. I did not look up what I should expect first, that would have spoiled the surprise. I got the analemma. My model only had a circular orbit! So, I think it is mostly due to the angle between
the ecliptic's normal and the earth's axis of rotation.
I guess the eccentricity of the earth's orbit will change the shape slightly, but that is only a teensy tweak.
Picture a stick pointing out of the earth, normal to the surface (I find some arbitrary temperate latitude easiest to visualise). Say the stick's projection onto the ecliptic points at the sun at midday one day, the mere fact of the axial tilt means that 24 hours later, it will not quite be pointing at the sun again.
Ok, how much of this is actual effect, and how much is artifact due to the "fixed time of photograph"? Since true noon (when we would expect a vertical line over the year due to the axis inclination) isn't happening at noon standard time every day of the year, we're shooting a picture of the sun either before or after it has passed it's zenith.
As for the position of the cross-over, that should be strongly dependent on the latitude of the observer, centered on the equator, and disappearing at high latitudes.
Ok, google imaged it, and the figure 8 never goes away, even at the pole, so I'm not sure if that would be the case on a more inclined planet like Mars (to explain the teardrop). But I did find that there's actually a state park devoted to this http://www.cerrilloshills.org/kiosk/kiosk.html (link spoiler safe, but leads to explanation if you can't wait for Ethan) not an hour drive from me. I see a science project coming up for my kid at some point.
Oops ... I didn't address the analemma on other planets! Due to the very short earth days (in comparison to the length of a year), we can see the sun drift left and right of the longitudinal plane at many points as we go through the equinoxes and the solstices. For planets with much longer days that effective sampling rate drops, and in the case of Mercury we get that single point.
The teardrop shape on Mars stumps me though since the effective sampling rate is about twice that of the earth's ... nor can orbital inclination and precession compensate (orbital inclination is too small, precession is too slow.) What am I missing (or does Mars have a whopping huge nutation?)
This is more fun than school ... even though I seem to make more mistakes than at school. Will we feature in a future article on "the wrong way people imagine things work?" :)
I think the image credit (first image) should go to Anthony Ayiomamitis, perhaps via Michael Strecker though I know it's been published elsewhere, I think on Anthony's own site.