"What we observe is not nature itself, but nature exposed to our method of questioning." -Werner Heisenberg
Looking down at the fundamental nature of matter, down past our cells and organelles, deep into the individual molecules and inside of the atoms that make them up, at long last, you get to things like the fundamental particles that make up all the known matter in the Universe.
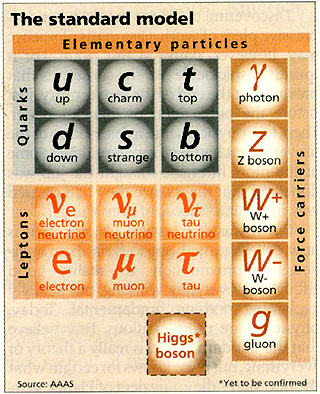
Things like electrons, photons, and the quarks that make up protons and neutrons, are all, as best as we can tell, fundamental particles. That means we can't break them up into anything smaller; they're not "made" of anything else.
And that's where things get weird.
Let's say I take some light -- what particle physicists call photons -- and I shine it through some slits. Two slits of finite width, two infinitely-thin slits, and one slit of a finite width. What type of pattern would I see?
Well, you'd see the classic patterns that come about because of two well-known and well-understood phenomena: interference and diffraction. Now it might seem weird to you, because these are properties of waves, but we can treat light like a wave without too much difficulty.
On the other hand, if we used something like electrons, you might expect a different result.
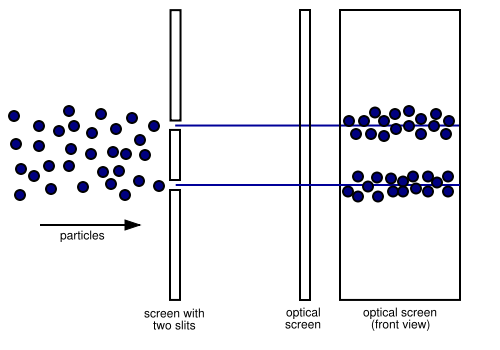
This is the result you'd get if you threw a bunch of tiny grains of sand at these two slits. Some grains go through one slit, some grains go through the other, and you wind up with two separate piles of sand on the other side.
So what happens when you send the electrons through? They make the interference pattern!
But we're clever, so what we do, to avoid the electrons from interfering with one another, is to send them through one-at-a-time. And over time, we count up what they're doing. Here are the results.

Unbelievably, each individual electron appears to interfere with itself!
So you go back and ask which slit each electron went through, like a good scientist would. So when you re-run the experiment, only this time you turn on a light to measure which slit the electron goes through, what do you find?
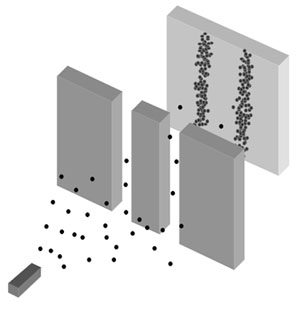
When you measure the electron, you destroy the interference pattern, and you force it to go through one slit or the other! It no longer interferes with itself, it no longer acts like a wave, and you just get the same pattern that you get for particles of sand.
The way you were likely taught this -- if you were taught this at all -- is that measuring the electron "collapses its wavefunction." And this is right... kind of.
Here's an -- as far as we know -- accurate depiction of what a helium atom looks like.

Now you might want to know where this electron is at any given instant. So you can shoot a photon at it. And the higher energy (i.e., shorter-wavelength) your photon is, the more accurately you can measure the electron's position. But you can never know it exactly. Why not?
Heisenberg's uncertainty principle! Not only can you never know something like "position" exactly, but the more accurately you measure its position, the less accurately you're allowed to know its momentum!
The same thing happens for energy and time. This is so spectacular that -- because E = mc2 -- particles that live for very, very small amounts of time have an inherent uncertainty in their mass! (If you ever hear a physicist talk about the "width" of a particle like the W or Z boson, or the top quark, this mass-uncertainty is what they're referring to.)
Is there a good, classical analogy for this? Sure there is; imagine a water balloon.

Imagine trying to measure exactly where the water balloon is in one direction. Well, you can't quite do it with just a ruler; a water balloon has a finite thickness to it. So what can you do? Well, you can squeeze it in one direction, and make it smaller.

But when you do this, it stretches in the other directions. The volume has to be conserved, or all the dimensions multiplied together cannot be less than a certain number.
That's what quantum mechanics is like. So you might wonder, with this in mind, what happens if you go back to your two-slit experiment, and only measure which slit the particles travel through a little bit?
Well, this experiment was just done (and other writeups are here and here), and what they can do is measure the average trajectory of the particles, but without destroying the interference pattern! In other words, if you look with low enough precision at whatever you're looking at, you allow the balloon to be "large enough," in some sense, in the direction that's important to the experiment.
But as far as nature goes? You never know either position, momentum, energy, or time exactly. The best you can do is to measure it well-enough to take away some of its options. The first double slit experiment was performed in 1799, and with new discoveries and measurements like this, we're likely to keep on playing with this setup for centuries to come.



Thankyou for making this simple.
Especially the electron path diagram.
Does this mean that time exists as quanta or can time still be continuous but our measurements are inexact?
I don't *like* the idea of quantized time, but my likes have never affected the world before.
time was invented to keep everything from happening in one instant. I think?!
Thanks for another fine article with concepts clear and simplified.
//So you go back and ask which slit each electron went through, like a good scientist would. So when you re-run the experiment, only this time you turn on a light to measure which slit the electron goes through, what do you find? //
Hmmm... I would be really interested in a snapshot of 70,000 electrons taken by this experimental set up (contrasting with your Fig. (d)). Where can I find it?
Ä°srail'de bir dini mahkeme, 20 yıl kadar önce dini hakimlere hakaret eden laik bir avukatın reankarnesi olmakla suçlanan bir sokak köpeÄine recm cezası verdi.
@Tom (Sorry that this is long)
Why Heisenburg:
The Heisenburg relations don't require quantised time or space. It requires something more confusing (but mathematically neat)
When an isolated system interacts with the rest of the world (eg. for us to measure something about it), the state of the system is changed. Awkward words like decoherence are used here, but the basic point is that the measurement has to give us a definite answer, and so the system ends up in a definite state for whatever we mentioned (eg. position or energy).
These changes are represented by operators (technically they have to work with complex numbers and be hermitian, but you probably don't care). The important point is this:
The order that the operators are applied in matters.
As an example, think about a book on a table, and the operations "spin by 90 degrees clockwise from above" and "flip over from left to right". The order matters.
The Heisenberg relation can be proven for any pair of operators with this property (called "non-commuting"). It doesn't say anything about the nature of space or time, just that these operators don't commute.
Is it just inexactness:
We can experimentally show that the problem isn't "inexactness" in our measurements. This goes by the name of Bell's inequality. You can prove that when we measure related things in a system with definite state (even with imprecise measurements), there are certain constraints on what we see. For example, if:
B occurs 50% of the time when A occurs, and C occurs 50% of the time when B occurs, then C must occur at least 25% of the time when A occurs. Observe that we could check all of these statistics looking at only 2 of A, B and C in any given test. Now in the real world, we can get things where:
B occurs 50% of the time when A occurs, C occurs 50% of the time when B occurs, but C never occurs when A occurs (We can only check 2 of them at a time). Hence there really isn't a definite state that we're measuring. It's not an exactness problem, the problem is that the way we heuristically think the world works is wrong.
This is easily the most lucid explanation of the Heisenberg Uncertainty Principle and the double slit experiment I've seen that doesn't require a lot of physics or math background. I have to show it to my parents. Lots of pictures are good, too. They should show this page to every high school student!
easily the most lucid explanation of the Heisenberg Uncertainty Principle and the double slit experiment I've seen that doesn't require a lot of physics or math background. I have to show it to my parents. Lots of pictures are good, too. They should show this page to every high school student!
Where is the "why" in the article? It demonstrates the issue and makes an analogy
"But when you do this, it stretches in the other directions. The volume has to be conserved, or all the dimensions multiplied together cannot be less than a certain number.
That's what quantum mechanics is like."
However, the analogy isn't strictly correct. It's just another way to roughly imagine the problem. Very roughly, since the Heisenberg relationship, as shown, applies only to certain pairs of variables that don't commute. Other variables whose operators do commute *can* be known at the same time. There's no "volume" being conserved.
A better explanation would be to show a 1-dimensions wave that extends far in both directions. This would have definite wavelength but no fixed position as it exists everywhere. You could combine wave of different wavelength, however, that add constructively in a small area but destructively elsewhere. The sum of the waves would therefore have a fixed position (where the waves are non-zero in a small region) but would no longer have a known wavelength (since we're now talking about a combination of a range of wavelengths). Pinning down one quantity requires formingn linear combinations of several values of the other. That's one way to view the why (especially where position and momentum are concerned, since momentum corresponds to the wavelength of the wave).
âbut the more accurately you measure its position, the less accurately you're allowed to know its momentum!â
But the uncertainty relation is concerned with precision, not accuracy: statistical spreads in the outcomes of repeated measurements on identically prepared states. IIRC it's a confusion of this sort and/or the measurement error one that leads to misleading¹ interpretations in terms of 'uncontrollable disturbances' and 'simultaneous' measurements.
¹ http://www.amazon.com/Lectures-Quantum-Theory-Mathematical-Isham/dp/186…
David
"A better explanation would be to show a 1-dimensions wave that extends..."
It's only an explanation if people can understand your explanation. you lost me in the first sentence, "1-dimensions wave"???
I was in the mood for a good Heisenberger this weekend but I wasn't sure where the vendor was....
This post reminds me of a favorite Heisenberg joke an older chemist told me last week,
Heisenberg is out for a drive and gets pulled over by a traffic cop,
Cop says, "Do you know how fast you were going?"
Heisenberg responds, "No, but I know where I am!"
My perspective is that the double slit experiment and other similar ideas is very easy to understand. If, for instance, a particle that spins or has motion within a field, will produce waves within the field if the field is dense with particles. The field we are discussing is the Zero Point Field (ZPF) and the theoretical particles/entities within it which have been proposed are, gravitons, quantum foam, Higg's particles, dark matter, etc. etc. etc. If an electron, for instance, were moving through such a physical medium they would produce waves of "particles" within the surrounding ZPF field like a boat moving through water or a spinning log in a stationary field. These waves would move though all open slits and interfere with the electron that only passed though a single slit, absolutely nothing mysterious about it if any of such particle exist.
For a photon which is also believed to be a particle, a similar explanation can be given. Spinning electrons that drop between energy states in an atom, produce EM radiation. If the EM radiation contains both waves of particles as explained above, accompanied by photons(which may be bundles of these same field particles) then the same explanation would apply and the double slit experiment totally loses any mystery at all to it.
Speculation: The factiz that for a reflection to occur inre a mirror there has to be an interaction of photons/electrons with the atomic particles/waves of whateveritiz that is the matter/energy (m/e) that comprises the mirror. A photon/electron does not merely 'bounce' off a mirror the same way a tennis ball bounces off a brick wall because the m/e of the mirror is porous/not 100% solid because of the 'space' between atomic nuclei and electrons as well as between atoms/molecules. This interaction process must take timeâoccur over a period of time. Causality is involved herein. The interaction has to consist of a change in the inertial/physical states of the atomic particles/waves within the mirror's m/e as well as a change in at least the inertial state of the photon/electron, possibly with the result being a new particle/wave, possibly a new photon/electron being released while the old photon/electron is somehow incorporated into the mirror's m/e system. In a similar way, there must be an interaction of photons/electrons with the m/e of whateveritiz that comprises the experimental apparatus necessary for a double slit experiment with the result that the original photons/electrons may not be those photon/electrons which eventually strike the target. How could we determine if the photons/electrons striking the target are the original photons/electrons or new/photons/electrons? Whatiz the possibility that the interaction process causes new patterns or changes in the old patterns of electromagnetic waves inre the m/e of the slit apparatus (the slitboxârhymes with sh_tboxâa little humor herein!) or perhaps in the spaces between the walls of the slitbox such that once a single photon/electron passed through a slit the next photon/electron would be caused to change its inertial state in a specific non-random way, e.g. in a predictable causal pattern?
I wonder what would happen inre interference patterns inside the slitbox if photons/electrons were shot past but parallel to the wall containing the slits in such a way that the photons/electrons as particles never entered the slitbox but as waves might influence activity within the slitbox and thereby cause changes in interference patterns within the slitbox. It may seem crazy to think that shooting photons/electrons past but parallel to the slits in a slitbox might influence the activity with the slitbox, but the factiz that many observed phenomena at the quantum level seem crazyânon-natural, so wondering Whatif? inre photons/electrons and slits inre slitboxes at least is not necessarily automatically 100% crazy.
Note: I prefer to use virgulingâthe use of slash-marksâto link concepts and principles such as matter and energy = m/e and photons and electrons = photons/electrons to conserve space and typing energy.
Note: I enjoy the visual humor inre (in regards) squeezing words together such as inre = in regards, in regards to, or relative to, factiz = fact is, etc., as if coining new words. Psychotics and neurotics tend to not see/not enjoy the humor while normals do.
I have to laugh, while I can relate to nothing scientific in this article, I was actually present for the waterballoon/funny face pic (9 from the top). I always enjoy seeing that pic - and all of it's spin offs - as it makes me feel like I was their for history!
Great article as always
-K-