"New stars offer to the mind a phenomenon more surprising, and less explicable, than almost any other in the science of astronomy." -George Adams
Welcome back to another Messier Monday here on Starts With A Bang! The Messier catalogue was the very first accurate deep-sky catalogue with over 100 objects, finally topping out with 110 in its final form today. Compiled in the 18th century by Charles Messier and his assistant Pierre Mechain, this collection of fixed, deep-sky objects contains 110 of the brightest, most easily found and most spectacular sight in the entire sky.
 Image credit: Tenho Tuomi of Tuomi Observatory, via http://rockpoint.dyndns.org/.
Image credit: Tenho Tuomi of Tuomi Observatory, via http://rockpoint.dyndns.org/.
Containing nebulae, star groupings, open star clusters, globular clusters, galaxies and more, there's no shortage of interesting objects to look at, although not all of them are visible at all times of the year. Today, I want to introduce you to one of the most overlooked Messier objects that's definitely worth a look at during the summer months, the newborn open star cluster Messier 21. Here's how to find it.
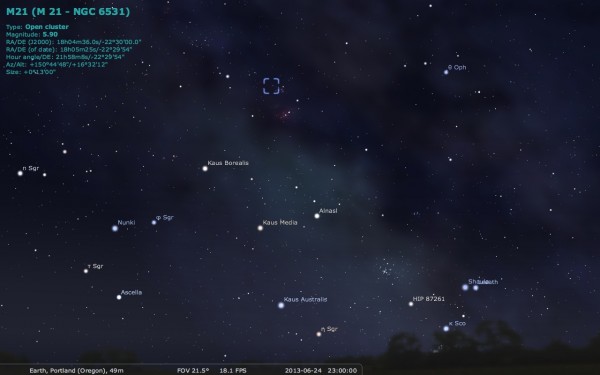
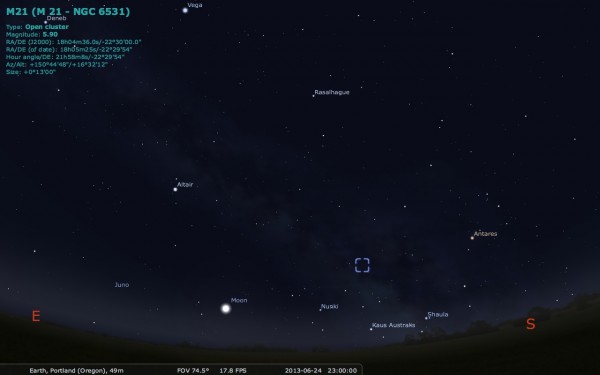 Image credit: me, using the free software Stellarium, via http://stellarium.org/.
Image credit: me, using the free software Stellarium, via http://stellarium.org/.
Throughout the summer, the three bright stars Altair, Deneb and Vega dominate a large swath of the overhead skies. Forming the Summer Triangle, they'll be high in the east after sundown tonight. But below it, far closer to the southern horizon, the asterism of the teapot (in the constellation Sagittarius) will rise about two hours after sunset. And if you can find that teapot, you're well on your way to finding Messier 21.
The tippy-top of the teapot is the star Kaus Borealis, prominent once it rises more than about 10 degrees above the horizon. And if you draw an imaginary line connecting the handle to Kaus Borealis and head about 6 degrees farther, just about 2.5 degrees to the west of the 4th-magnitude star μ Sagittarii, you'll find the dense open cluster Messier 21.
If this sounds familiar to you, it's because these are practically the same instructions for finding the Trifid Nebula (Messier 20), located less than one degree away! In fact, they look delightful together in the same field of view.
 Image credit: RoryG of http://eastexastronomy.blogspot.com/.
Image credit: RoryG of http://eastexastronomy.blogspot.com/.
The Trifid Nebula is one of the youngest star-forming regions in the entire galaxy, as some of the stars in it may be just hundreds of thousands of years old. Well, it turns out that Messier 21 is a very, very young open star cluster! You might wonder -- since they're so close together -- whether these two objects are related.
When we take a look at Messier 21 in detail, here's what we find.
The first remarkable thing about this cluster? It's small. While most open clusters have somewhere around 1,000 stars in them, M21 has only about 57 stars. That's a number fit for a ketchup, not for a star cluster!
So you might wonder if this is a very old cluster that's been around for a long time, and only a few stars are left, having survived the intense gravitational forces that cause a cluster to break up on timescales of hundreds of millions of years.
 Image credit: © 2006 - 2012 by Siegfried Kohlert of http://www.astroimages.de/.
Image credit: © 2006 - 2012 by Siegfried Kohlert of http://www.astroimages.de/.
No. Not a chance, actually. Contrary to what you might guess, this is one of the youngest star clusters in the entire galaxy! The above image really brings out the color, and as you can see, it's bright, blue stars that predominate in this cluster. Well, since we use the color-magnitude relation to determine how old the oldest surviving stars are in a cluster, we can figure out that this object is only 4.6 million years old. That's just 10% the age of the Pleiades, the prototype for a "young open cluster," and just 0.1% the age of the Sun!
There might not be any O-stars left, but the brightest of all B-class stars can be found here, meaning there's still a chance for a Type-II supernova in this cluster.
The infrared image of this cluster verifies the young age here, as you can see by the intense blueness of the central stars, courtesy of the 2-Micron-All-Sky-Survey. With practically no intervening gas or dust, this must have been a small fragment of a larger cluster that formed relatively quickly and burned the bulk of its dust off. At just 13 arc-minutes in diameter, it's quite compact, and at an estimated distance of some 3,000-4,200 light years, it's only about 11-to-16 light years across. That's a tiny distance for so many bright, hot, young blue stars!
So, how does that compare to the neighboring Trifid Nebula?
 Image credit: Fred Espenak of http://astropixels.com/.
Image credit: Fred Espenak of http://astropixels.com/.
The Trifid is at least 1,000 light years farther away, although there was some controversy until the Spitzer Space Telescope took a look at it. Unfortunately, there are very few high-quality observations of the open cluster Messier 21, so I can't show you, for example, a spectacular Hubble image.
But I can show you a spectacular shot from Pan-STARRS!
 Image credit: Eugine Magnier (UH IfA), Peter Draper & Nigel Metcalfe (Durham University), ©PS1 Consortium.
Image credit: Eugine Magnier (UH IfA), Peter Draper & Nigel Metcalfe (Durham University), ©PS1 Consortium.
Including both the Trifid and the Lagoon nebula as well as M21, this is some real eye candy for all of you. Yes, all of these fall in the galactic plane, where clusters, nebulae, star-forming regions and other Messier objects are most common.
But I was able to isolate Messier 21 all by itself by finding a zoomable version, and here it is in all its glory!
 Image credit: Eugine Magnier (UH IfA), Peter Draper & Nigel Metcalfe (Durham University), ©PS1 Consortium.
Image credit: Eugine Magnier (UH IfA), Peter Draper & Nigel Metcalfe (Durham University), ©PS1 Consortium.
Part of a spectacular part of the Sagittarius arm of our galaxy known as the Sagittarius OB1 Stellar Association, these stars -- and the cluster in general -- is sorely in need of further study; who knows, maybe this will inspire people to take a deeper look at this all-too-often overlooked deep-sky wonder! It was discovered by Messier himself in 1764, meaning that next year will be the 250th anniversary of this object.
And that’ll do it for another Messier Monday! Including today’s entry, we’ve taken a look at the following Messier objects:
- M1, The Crab Nebula: October 22, 2012
- M2, Messier’s First Globular Cluster: June 17, 2013
- M5, A Hyper-Smooth Globular Cluster: May 20, 2013
- M8, The Lagoon Nebula: November 5, 2012
- M13, The Great Globular Cluster in Hercules: December 31, 2012
- M15, An Ancient Globular Cluster: November 12, 2012
- M20, The Youngest Star-Forming Region, The Trifid Nebula: May 6, 2013
- M21, A Baby Open Cluster in the Galactic Plane: June 24, 2013
- M25, A Dusty Open Cluster for Everyone: April 8, 2013
- M29, A Young Open Cluster in the Summer Triangle: June 3, 2013
- M30, A Straggling Globular Cluster: November 26, 2012
- M33, The Triangulum Galaxy: February 25, 2013
- M37, A Rich Open Star Cluster: December 3, 2012
- M38, A Real-Life Pi-in-the-Sky Cluster: April 29, 2013
- M40, Messier’s Greatest Mistake: April 1, 2013
- M41, The Dog Star’s Secret Neighbor: January 7, 2013
- M44, The Beehive Cluster / Praesepe: December 24, 2012
- M45, The Pleiades: October 29, 2012
- M48, A Lost-and-Found Star Cluster: February 11, 2013
- M51, The Whirlpool Galaxy: April 15th, 2013
- M52, A Star Cluster on the Bubble: March 4, 2013
- M53, The Most Northern Galactic Globular: February 18, 2013
- M60, The Gateway Galaxy to Virgo: February 4, 2013
- M65, The First Messier Supernova of 2013: March 25, 2013
- M67, Messier’s Oldest Open Cluster: January 14, 2013
- M72, A Diffuse, Distant Globular at the End-of-the-Marathon: March 18, 2013
- M74, The Phantom Galaxy at the Beginning-of-the-Marathon: March 11, 2013
- M78, A Reflection Nebula: December 10, 2012
- M81, Bode’s Galaxy: November 19, 2012
- M82, The Cigar Galaxy: May 13, 2013
- M83, The Southern Pinwheel Galaxy, January 21, 2013
- M86, The Most Blueshifted Messier Object, June 10, 2013
- M92, The Second Greatest Globular in Hercules, April 22, 2013
- M97, The Owl Nebula, January 28, 2013
- M102, A Great Galactic Controversy: December 17, 2012
- M104, The Sombrero Galaxy: May 27, 2013
Come back next week, where we'll return to the Summer Triangle for another spectacular treat from Messier's catalogue, only on Messier Monday!




M21 IS THE LOCATION OF TIKA.REF;GOLDEN PYRAMID OF TICA.JUST FINISHED RESEARCH OF 25 YEARS.100 PERCENT CORRECT.