“If you see an antimatter version of yourself running towards you, think twice before embracing.” -J. Richard Gott III
It may not occur to you that it's a special thing that the Earth and everything found on it is made of matter; it seems intuitive that it couldn't be any other way. And yet, the very laws of nature themselves haven't yet told us why or how the Universe is this way! For this week's Ask Ethan (and leave your own questions or suggestions here), our regular reader Michael Fisher wants us to get at the heart of this, asking:
Is it true that in the early universe matter & antimatter were created in equal amounts? And if not do we know why there was a difference?
If they were created in equal amounts how is it we are left with one particle per billion of matter with very little [or no?] antimatter remaining? In other words ~ do we have a mechanism to explain the dominance of matter over antimatter in our observable universe?
Think about this for a minute, if you will.
 Image credit: Greg Parker, via http://www.newforestobservatory.com/.
Image credit: Greg Parker, via http://www.newforestobservatory.com/.
This is (a little bit of) our Universe. Hundreds of billions of stars and star systems within our galaxy alone; hundreds of billions of galaxies within our observable Universe. Out of all the possibilities, we've only directly explored our own star system, which it turns out -- to no one's surprise -- is made of matter and not antimatter.
But, as far as we can tell, being made of matter and not antimatter is something that's true of everything in the Universe! More specifically, there's stuff everywhere in the Universe, and if there was a part of the observable Universe that was made of antimatter, we would see catastrophic results where the matter and antimatter meet!
 Image credit: Andrew Harrison of http://interstellar-medium.blogspot.com/.
Image credit: Andrew Harrison of http://interstellar-medium.blogspot.com/.
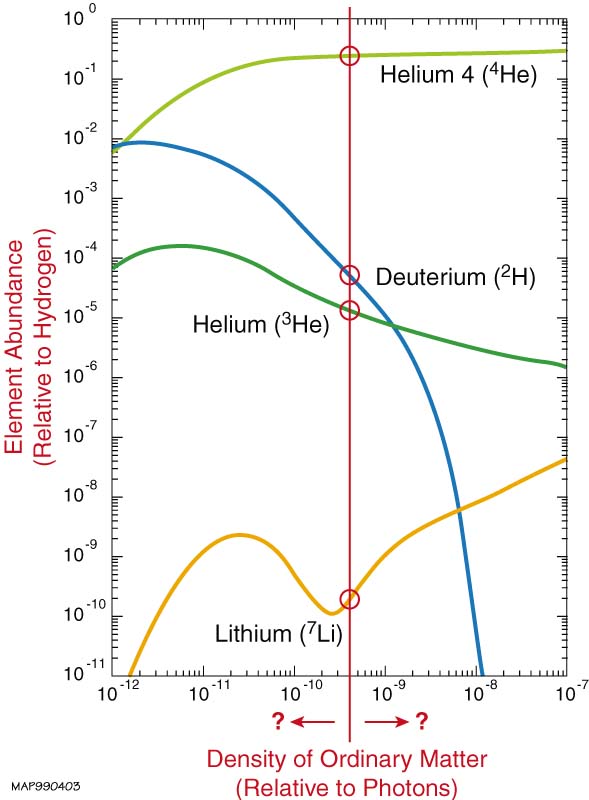
For example, the interstellar medium -- the space between stars in galaxies -- is full of material, even if there aren't any stars in many regions. Space is vast, of course, and the density of matter is sparse, you might be wondering if you threw a single antimatter particle (say, an anti-proton) into the mix, how long it would last before running into a particle of matter an annihilating, on average. In our own galaxy's interstellar medium, the mean lifetime would be on the order of about 300 years, which is tiny compared to the age of our galaxy! This huge constraint tells us that, at least by us, the amount of antimatter that's allowed to be mixed in with the matter we observe is at most 1 part in 1015!
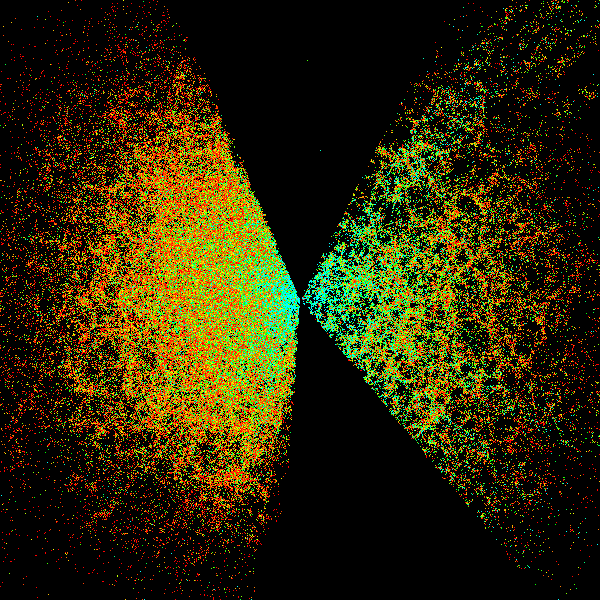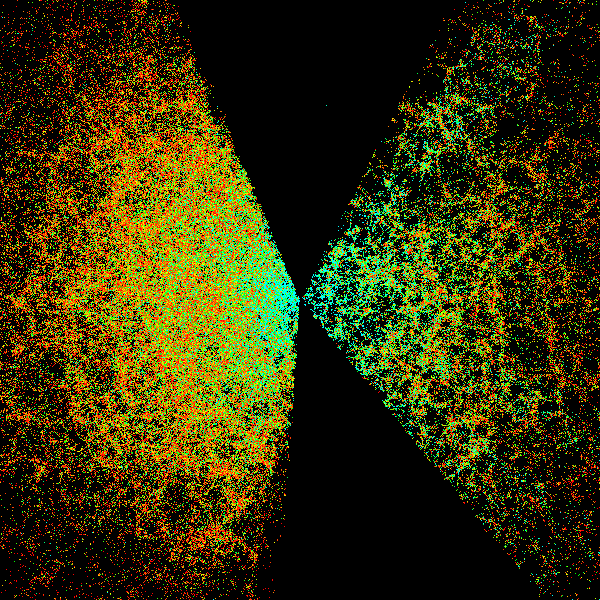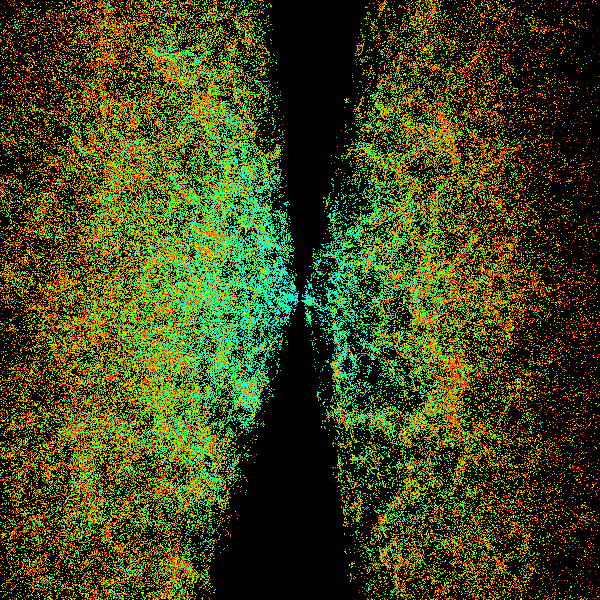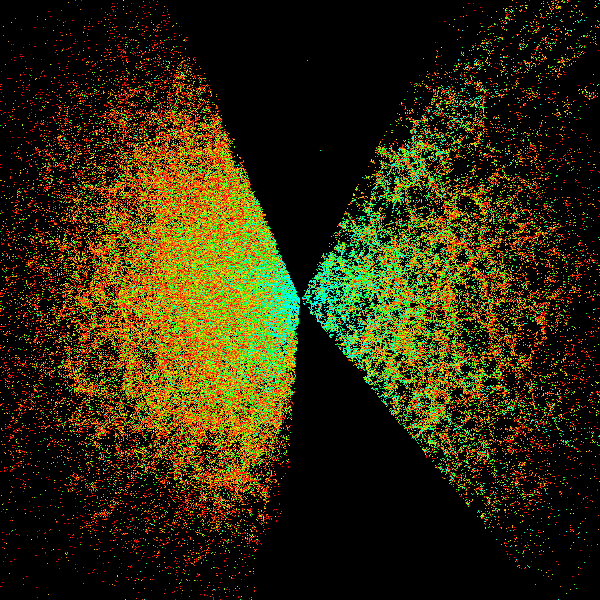 Image credit: Sloan Digital Sky Survey (SDSS), via http://astro.u-szeged.hu/.
Image credit: Sloan Digital Sky Survey (SDSS), via http://astro.u-szeged.hu/.
On larger scales, we've now mapped out galaxies and galaxy clusters to huge distances, and taken detailed looks in many different wavelengths, including visible light, infrared, microwave, radio, ultraviolet, X-ray and gamma-ray wavelengths. In particular, X-ray and gamma-ray observations are hugely important, because when matter and antimatter meet each other and annihilate, they emit characteristic high-energy radiation that would be detectable to our great observatories.
With 55 galactic clusters well-measured under our belt, from just a few million light-years to over three billion light-years away, we've seen that even on large, cosmological scales, 99.999%+ of what exists in our Universe is matter and not antimatter.
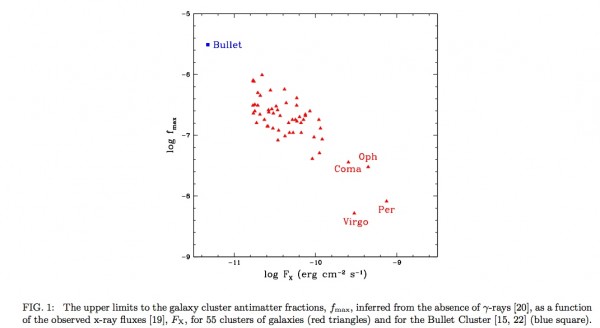 Image credit: Gary Steigman, 2008, via http://arxiv.org/abs/0808.1122.
Image credit: Gary Steigman, 2008, via http://arxiv.org/abs/0808.1122.
The overwhelming conclusion is that everything we see in our Universe is made predominantly out of matter, not antimatter.
And yet, in many ways, this is a huge surprise! You may know that E = mc2, and that tells you that not only does mass, inherently, have a certain amount of energy to it, but that you can create a particle with a given mass if you have enough energy to do it, and that energy is given by Einstein's most famous equation. But there's a little more to the story than that.
You see, as far as we've been able to produce reactions between fundamental particles in laboratory-and-observatory conditions here on Earth, the only way to create matter is by taking twice the amount of energy that E=mc2 would require, and creating equal amount of both matter and antimatter. And conversely, the only way we've ever found to destroy matter is by colliding it with its antimatter counterpart, producing pure energy as a result. All the laws of physics -- all the reactions and interaction ever discovered -- indicate that this is the case at all energies and at all time.
And yet, then there's our Universe.
If we started off our Universe with a hot Big Bang, after the end of inflation, with all the right initial conditions and all the known laws of physics and nothing else, we'd have an early state that was perfectly in-line with our expectations:
- The Universe would be hot, dense, expanding, and full of radiation and equal parts matter-and-antimatter.
- Matter and antimatter would sometimes collide, annihilating into radiation, while high-energy particles would also sometimes collide, spontaneously creating new particles of matter-and-antimatter, in equal amounts, with that excess energy.
- The Universe would expand and cool, and as it did, energies and densities would drop.
Those last two parts -- energies and densities dropping -- leads to a race.
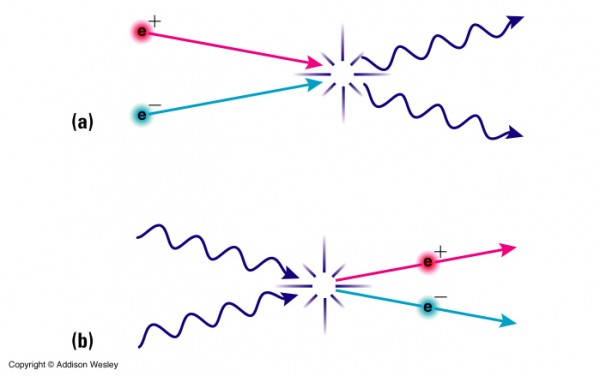
As energies drop, it gets harder and rarer for high-energy particles to produce new matter/antimatter pairs (b), decreasing the ratio of matter-(and-antimatter)-to-radiation in the Universe. But as densities drop, it gets harder and harder for matter/antimatter pairs to find one another (a), which means that the ratio will never drop all the way to zero; there will always be some matter (and antimatter) left in these scenarios.
And that's where it gets odd. Because if we just stick to the known laws of physics and the reactions we've seen, we'd expect that there'd be about 1020 particles of radiation for every one particle of matter (or antimatter). But in our Universe, there are "only" about a billion -- or 109 -- particles of radiation for every one particle of matter (something we can tell by measuring the photon-to-baryon ratio indirectly, via the CMB), and the amount of antimatter is much lower.
So where did all this extra matter come from? Why was it extra matter that was created and not extra antimatter? And when did it happen, and how did it happen?
Michael (and everyone), I'm going to be honest with you: this is one of the biggest unsolved puzzles in all of physics today. But not knowing everything doesn't mean we don't know some really important clues. It's been known since the 1960s, for instance, that so long as you fulfill these three famous criteria:
- Out-of-equilibrium conditions,
- Baryon-number-violating interactions, and
- C- and CP-violation,
you not only can create more matter than antimatter (or vice versa), but an asymmetry is inevitable. And, as luck would have it, two of these criteria are very easy to satisfy.
 Image credit: Shutterstock / Designua, retrieved via http://www.gizmag.com/.
Image credit: Shutterstock / Designua, retrieved via http://www.gizmag.com/.
"Out-of-equilibrium conditions" would be something where, if something happens in one part of a system, there are other parts of the system that will be unaffected by what's happening, as that information can't reach it in a timely manner. The expanding Universe is a perfect example of a system that's out-of-equilibrium by definition, and the description I gave you above of matter/antimatter creation-and-annihilation as the Universe expands and cools is a perfect example of an out-of-equilibrium process.
So that one's easy.
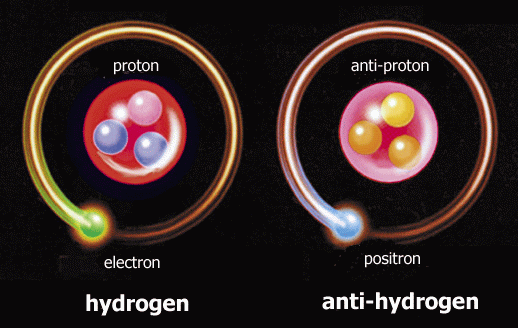
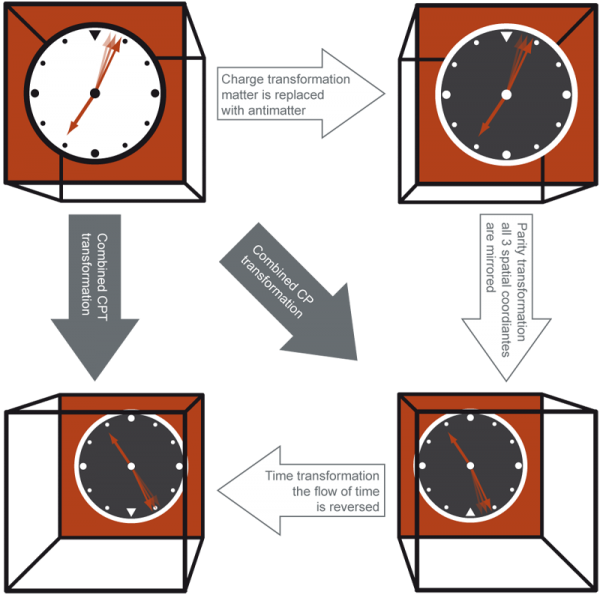 Image credit: SMI / Hyperfine Structure of Antihydrogen, via http://www.antimaterie.at/.
Image credit: SMI / Hyperfine Structure of Antihydrogen, via http://www.antimaterie.at/.
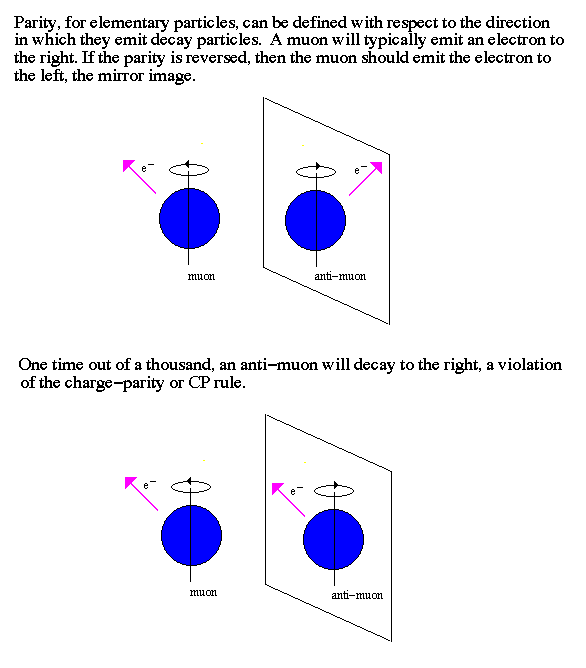
We also know that there are many fundamental examples of how matter and antimatter can differ from one another, and how certain symmetries are broken. One of these ways is charge conjugation (C) symmetry, where you replace all the particles with antiparticles; if C-symmetry is conserved, the particle-and-antiparticle systems will behave the same way. Another of these ways is parity (P), or mirror-image symmetry; if P-symmetry is conserved, the real system and the mirror-image system will behave in the same way.
If you have an unstable particle -- like a spinning muon -- it's going to decay in a very particular way: by ejecting an electron in a certain direction relative to its spin. If you reflect that muon in a mirror (P), it's going to appear to eject the electron in the opposite direction relative to its spin, something that doesn't happen in real life. If, instead, you replace that spinning muon with a spinning anti-muon (C), it would eject a positron in that original direction, also something that doesn't happen in real life. But if you replace the spinning muon with a spinning mirror-image anti-muon (C and P together, or CP), you'd hope that this decay happened just as reliably as a muon would decay in the real (non-mirror) world. But it doesn't, and there are other examples of how C and CP are violated, including in Kaon and B-meson systems.
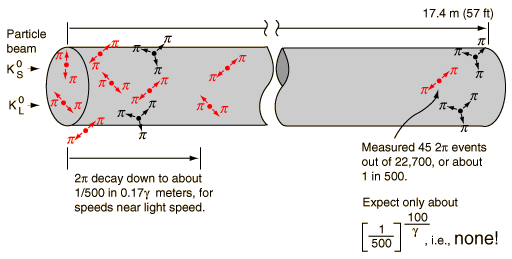 Image credit: R. Nave of http://hyperphysics.phy-astr.gsu.edu/.
Image credit: R. Nave of http://hyperphysics.phy-astr.gsu.edu/.
So all we need is for an interaction that violates baryon number in sufficient amounts, or, in other words, create baryons where there were none (but there were other things) before. Unfortunately, that requires some physics beyond the physics that's known, and a part of our Standard Model!
But, there are many known mechanisms that could allow us to make this happen, including:
- From grand unified theories containing new GUT-scale particles,
- From theories with new scalars that contain the Affleck-Dine mechanism,
- From extensions of the standard model that include heavy, sterile neutrinos,
- From a lepton excess in the early Universe (leptogenesis, for the experts), and
- From new physics at the electroweak scale that could enhance the matter/antimatter asymmetry found in the Standard Model.
I'm going to walk you through one example (that I've detailed in the past and alluded to twice before) just for illustrative purposes.
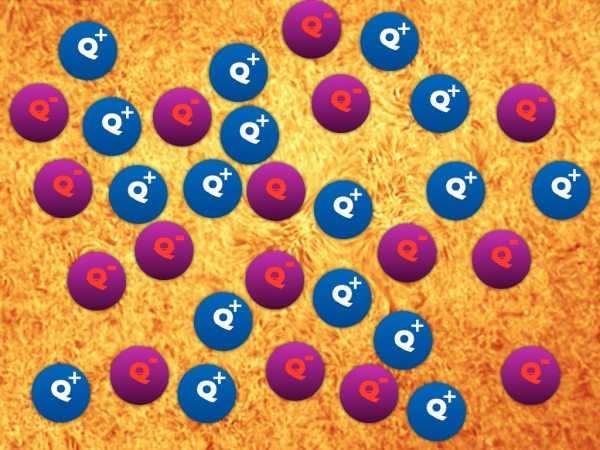
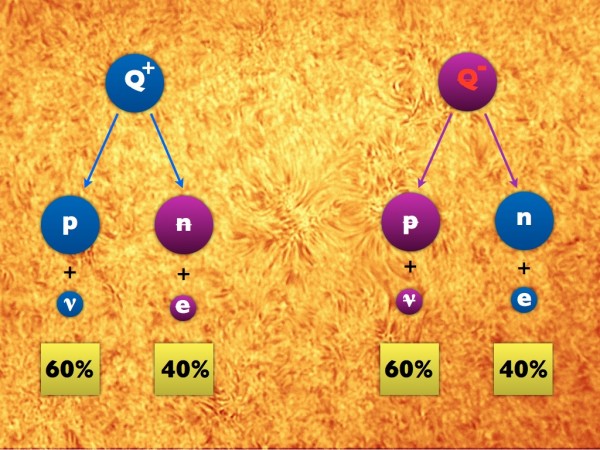
Imagine the hot, dense, young Universe, and imagine that in addition to all the radiation and the matter-and-antimatter particles found in the Standard Model flying around, there's also a new particle (and antiparticle), the Q (and the anti-Q). The Q is massively heavy (much heavier than a proton), has a positive charge of +1 (the same as the proton charge), and gets created in great abundance in the early Universe, along with its antimatter counterpart the anti-Q, which has the same mass as the Q but the opposite charge.
Since they're both unstable, when the Universe cools enough, we're going to stop making new ones eventually, and while most Qs and anti-Qs will find each other and annihilate, the ones that remain after that will simply decay.
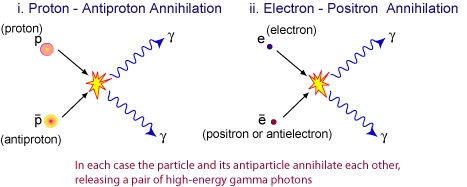
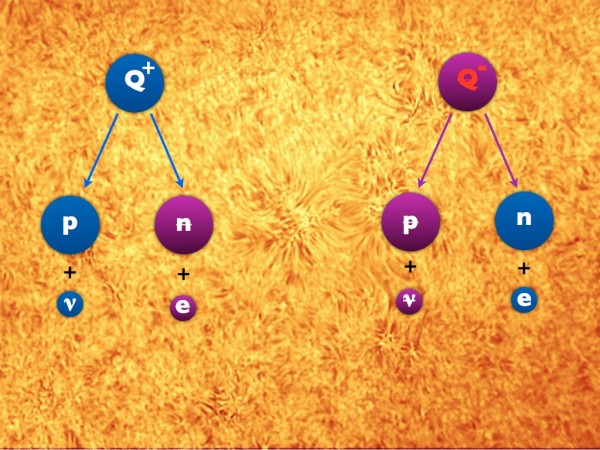
For every decay that can happen to a Q, the antimatter counterpart must happen for the anti-Q. If a Q decays into a proton and a neutrino, the anti-Q must decay into an antiproton and an antineutrino. If a Q decays into an antineutron and a positron, the anti-Q must decay into a neutron and an electron.
(These aren't real particles -- the Q and anti-Q are totally made up for illustration -- but there are examples of particles, such as the X-and-Y bosons in GUTs, or leptoquarks in some Standard Model extensions, that follow very, very similar rules.)
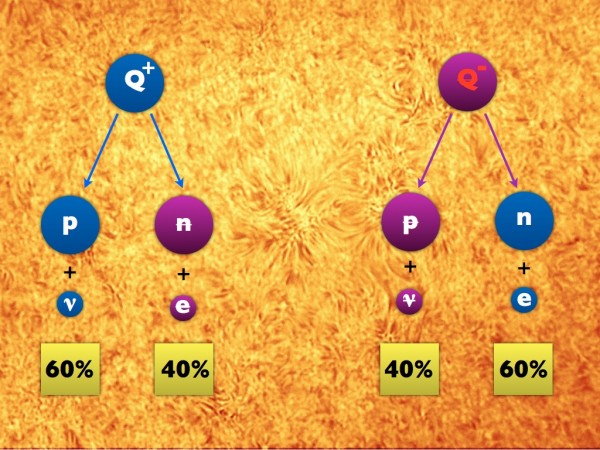
If there were no CP-violation, they'd decay in the exact same way as one another.
And this is very boring; it wouldn't create a matter excess, for one. But if you allow for CP-violation, one of the things that can be different between particles and antiparticles is what we call the branching ratio, or what percent of Qs decay into protons/neutrinos vs. what percent of anti-Qs decay into antiprotons/antineutrinos. So we could have something like the following, which is similar to what we see in Kaon/B-meson systems. Note the differences between the decays of the Qs and anti-Qs; you may have to look at it for a second to see the difference.
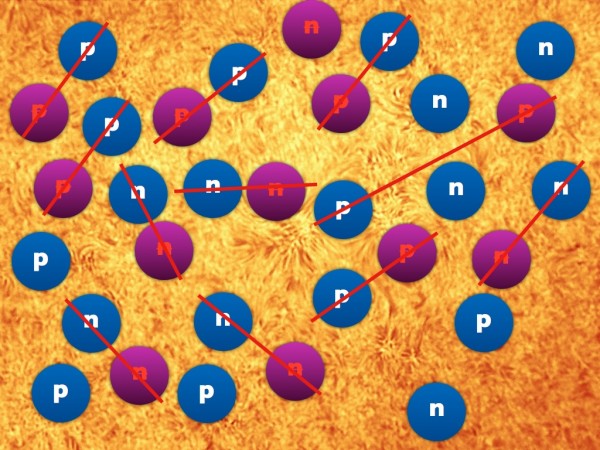
So let's assume we had a Universe full of matter and antimatter in equal parts and radiation, which we ignore. Let's also assume that there were a bunch of Qs and anti-Qs in equal numbers, which decayed according to the CP-violating rules above.
What would be left?
A sea of protons, neutrinos, antineutrons, positrons, antiprotons, antineutrinos, neutrons and electrons, for sure. But -- and here's the key -- there would be more protons-and-neutrinos than there would be antiprotons-and-antineutrinos, and there would be fewer antineutrons-and-positrons than there would be neutrons-and-electrons. If we ignore the leptons (neutrinos, electrons and their antimatter counterparts), this is what a sea of Qs and anti-Qs decaying would give us.
And after the matter-antimatter pairs all find one another, that's what we'd have left: an excess of matter over antimatter!
And some variation of that is almost definitely where the matter-antimatter asymmetry came from, and why every place in the Universe appears to have the same density of matter (and not antimatter) no matter where we look! Even though this is one of the greatest unsolved problems in all of physics, we still know an awful lot about it, and that's a story worth telling!
So congratulations, Michael, we owe you a prize (and you owe me your address), and if you'd like a chance to win one of three remaining prizes (or just have a question you'd like to see featured on Ask Ethan), ask us here!


Excellent post as always.
Typo spotted in second last paragraph - should read "And some variation of that is almost definitely where the matter-antimatter *a*symmetry came from...".
Thanks Ethan
I'm well chuffed! Emailing you the delivery details in a moment
Haven't quite got my head around this article yet ~ going to take some concentration!
I have many other questions too so I'll fire them in your direction when I've figured out how to put them in words [not easy]
Michael
On the other hand maybe there is something that keeps matter and antimatter from annihilating each other that we don't understand. Perhaps it is not easy for us creatures of matter to detect antimatter and there really is a equivalent and equal antimatter universe all around us. :)
Why would there be such a thing which has NEVER been observed, even though we've managed to make lots of antimatter, Kenny?
matter is a construct of solitons - think tightly bound little vortexes of pure motion force (motion itself is the fundamental quanta and not merely an attendant property of forces or objects)
any particle of matter is like a flame - a self-sustaining reaction that achieves stability for an extended period so long as conditions are right
this is the reason that at ever higher energies in atom smashers particles live ever shorter lives - as you subdivide matter, the whorls of solitons more easily spin out
as for the dominance of matter over anti-matter, it is about handedness - our universe itself has a dominant direction of spin
author, The Fundamental Quanta c 1987
Yeah, sorry, that's about the same level as the quantum fluctuations in dilithium crystals make warp travel possible.
All the antimatter is gone? So no easy place nearby to fill up my NCC-1701D? Damn... :/
For more detail, try:
The mystery of the missing antimatter / Helen R. Quinn and Yossi Nir ; illustrations by Rutu Modan.
Publisher Princeton, N.J. ; Woodstock : Princeton University Press, c2008
Not to worry, it won't be invented for about 80 years yet, if the movies have it right...
For a non-physicist and non-mathematician oldster like myself, all this matter/anti-matter is essentially theoretical stuff, that may or may not be actually what it is at all. (Interesting to think about, to posit etc., but not too often.) Science, however, is like that, I suppose, and if one doesn't ask questions about ideas, no one will seek answers. Yes?
You say "some variation of that is almost definitely where the matter-antimatter asymmetry came from."
That's hubris. The cosmic imbalance of matter over antimatter is one of the great mysteries of nature, and you have no basis in claiming that a particular speculation is "almost definitely" the answer.
Your writing is very good and very valuable, but a little more humility in such matters might be best.
For a discussion of other cosmic mysteries:
The 9 Greatest Mysteries of the Universe
IMHO you've missed the trick, Ethan. See Mark Hadley re CP violation. And see that CSIRO picture? Think of the early "cooking-pot" universe where photons turn into electrons & positrons and protons & antiprotons, and vice-versa. On top of that particles can be individually melted into the background plasma as per this physicsworld Brookhaven article. Now think of mixed-doubles tennis. One side is going to win. It doesn't matter how evenly matched they are, one side will win in the end. Then take a look at Jim Mitroy's article on positronium, which "can be regarded as a sort of light hydrogen atom”. Think about that. Then remember that baryon asymmetry is matched by lepton asymmetry.
The reason why this problem exists is that people label particles as matter and antimatter, and pairs of particles as matter or antimatter. That's inconsistent, as is labelling the proton as matter when actually it's more like the positron than the electron. To be consistent, you label the proton as antimatter rather than matter. Then the problem goes away.
"You say “some variation of that is almost definitely where the matter-antimatter asymmetry came from.”"
Uh, who said that?
"That’s inconsistent, as is labelling the proton as matter when actually it’s more like the positron than the electron."
Except for being 1000 times more massive and being composed of three other components compared to the positron's 1, and having some extent whilst the positron and electron have not yet displayed any semblance of extent in space.
What happens when a proton and antineutron meet? Do the individual up and down quarks and antiquarks annihilate, leaving behind an extra up quark and down antiquark?
Proton is uud.
Neutron is udd.
Anti-neutron is anti-up/anti-up/anti-down.
Remaining: anti-up and down.
Which particle is that? A muon of some type. They tend not to be stable.
QUOTE from comment #4 by Wow "...we’ve managed to make lots of antimatter..."
Hi WOW. I got this from the Wiki on antimatter:- One researcher of the CERN laboratories, which produces antimatter regularly, said:
If we could assemble all of the antimatter we've ever made at CERN and annihilate it with matter, we would have enough energy to light a single electric light bulb for a few minutes.
How much antimatter have we made in total [even if it existed for only an instant] & does it justify the term "lots"?
QUESTIONS FOR ANYBODY
1] Is there a hypothetical process by which we could manufacture & contain pellets of NON-CHARGED antimatter for later use as a fuel? I wondered if we could cool same types of antimatter [elements & compounds?] sufficiently for superconducting properties to come into play & then we could suspend it in an electromagnetic field in a vacuum vessel. I imagine the path from creating the particles [or atoms] to a containable very cold pellet would be difficult or impossible & perhaps not an efficient process
2] Supposing we could do 1] for arguments sake ~ would contained pellets of antimatter be a useful & efficient fuel? For example:- if we arranged for a tiny pellet of matter & antimatter to interact a portion of the energy released would be in the from of neutrinos ~ which we can't trap, thus wasted energy
3] If we wished to build a robot [no health & safety concerns!] space vehicle with its own on-board fuel supply [no sails to catch natural or man made external energy beams] & we wished to convert the fuel to thrust directly or indirectly via say ion engines. What is the fuel with the highest thrust to mass ratio when one allows for the containment of the fuel & the conversion process? I'm thinking that antimatter [imagine we can make it no problem] may be a poor option because of...
a] complexity & mass of the containment mechanism
b] equal amount of matter fuel needed to interact with the antimatter fuel
c] efficiency losses due to some portion of the energy produced not being direct-able aft-wards to produce usable thrust
d] efficiency losses if the energy produced has to be converted to say electricity to drive say an ion motor
Cheers!
@John Duffield #12: Once again, you have picked out some quotes, misunderstood them, mixed them with your other misunderstandings, and declared all problems in physics solved.
Labelling the proton as antimatter, even though it's made of quarks? You've revolutionised physics. All we have to do is "think about it". No math necessary!
Do the Nobel committee know about you? The prize is surely yours...
@Michael Fisher: How much antimatter have we made? If you mean "whole atoms" (anti-atoms), I think the number runs into the thousands, in experiments at CERN and Fermilab.
If you mean antiprotons or antielectrons, the number is much larger, but still not macroscopic.
The Tevatron at Fermilab operated from 1983 to 2011, colliding beams of protons and antiprotons. The antiproton beam had roughly 10^12 antiprotons circling, with a lifetime (1/e) of roughly 24 hours. Assuming a nominal "beam year" of 10^7 seconds, that's about 10^14 antiprotons per year for 28 years.
More or less, that's about a nanoavogadro of antiprotons :-)
@Ethan: Do you have a recent reference for "direct" cosmological limits on antimatter density?
The best I ever found was a really cool 1996 CERN report, which gave a limit of 10^-7 out to the nearest 20 Mpc. This was done with a ladder of limits from solar system models, through the Sun's motion through the ISM, galactic clouds, cosmic rays, etc.
Cosmologically, BBN and the baryon/photon ratio gives the few ~ 10^-10 limit you quote, but that doesn't address the possibility of AM "clumping" on scales of different superclusters, separated by voids.
If you know of good limits on scales larger than a few Mpc, I'd be really interested to read them. CP violation (in B-antiB mesons) is what I spent the first decade of my career working on, and our current best results are many orders of magnitude too small to satisfy the Sakharov conditions.
Hey Ethan,
Could you explain how matter collapses from a probability wave into matter and how that collapse propagates?
ie: When you open the door to Schrodinger's cat box and does the nose become real first or does the entire system collapse from superstate simultaneously? Or can the system not help but be real before opening the door because of decoherence?
10^17 is still a lot. You try counting it!
The production and the detection of such things do not include the effects of some force that keeps them apart and yet they've not yet found any evidence in all those events of such a force.
Either it's so impotent it doesn't appear above the noise level (and the discernment of these apparati are high indeed), or it doesn't exist.
It's a bit like if quantum tunneling was incorrect. Experiments on it may not be too common, but the effects of it AS IS are used, therefore any change to how it works would have been noticed in the items we use that rely on it.
darkgently: I've merely applied some simple logic that you can't refute. Quarks are a red herring. We've never seen a free quark, and don't forget the Bs meson. It's comprised of a bottom antiquark and a strange quark, so it isn’t really matter or antimatter, it’s both. And it oscillates into its own antiparticle and back in about 18 picoseconds, so again it’s both. Positronium is both too. And it's like hydrogen. And baryon asymmetry is matched by lepton asymmetry. But if you prefer to wallow in mystery I can't stop you.
Wow: the proton is more like the positron than it's like the electron. And the electron has demonstrated extent in space because its field is what it is. It's quantum field theory, not quantum point-particle theory. Everything is field and waves or excitations if you prefer.
"darkgently: I’ve merely applied some simple logic that you can’t refute"
Uh, john, he did just that.
Or is this a fact you can't refute therefore don't even bother to try?
"We’ve never seen a free quark"
You've never seen the inside of a brick, either. You've never seen an electron. You've never seen a free neutron. You've never seen a black hole.
You've never seen tomorrow.
No-see-ums can exist, therefore insisting something has never been seen is not proof it doesn't exist.
"It’s been known since the 1960s, for instance, that so long as you fulfill these three famous criteria:
- Out-of-equilibrium conditions,
- Baryon-number-violating interactions, and
- C- and CP-violation,
you not only can create more matter than antimatter (or vice versa), but an asymmetry is inevitable."
OK that's fine but what physicist seems to avoid answering is: With these three conditions; IS IT ALSO possible to create more antimatter than matter and hence get a different type of asymmetry? In particular by using neutrions and anti-neutrinos of the opposite spin as observed in our visible universe.
That is my question? Or is it impossible to create the reverse asymmetry of our observed universe? Even if I start out with neutrinos and anti-neutrinos that have the opposite spins that they have in our observable matter universe.
"Wow: the proton is more like the positron than it’s like the electron."
No, the only and I mean ONLY thing they have in common is the total net charge of them.
EVERYTHING ELSE is different.
You have lungs?
A lungfish has lungs.
Therefore you're a lungfish!
Or you have more in common with the lungfish than you have with a dead ape.
"OK that’s fine but what physicist seems to avoid answering is: With these three conditions; IS IT ALSO possible to create more antimatter than matter and hence get a different type of asymmetry?"
No, every physicist will answer it, though most think it entirely tautological and therefore pointless.
No.
By definition: antimatter is that matter which we don't see normally.
If the violation had put what we consider antimatter as the residuum, then we would have defined that antimatter to be matter and the matter we consider matter now to be antimatter.
How is the left or right side of a muon or other particle defined? I get that spin is one axis (drawn as vertical). But what defines forward, backward, left and right?
re my #25 and Wow's response #28
Now Wow you miss my point. No you don't miss it; you just disagree with me. Which is fine.
But for those who did miss my point; I didn't have time before to find the following quote to better frame my question.
Stephen Hawking says, "There is a mathematical theorem that says that any theory that obeys quantum mechanics and relativity must always obey the combined symmetry CPT. In other words, the universe would have to be have the same if one replaces particle by antiparticle, took the mirror image, and also reversed the direction of time." The Illustrated A Brief History of Time, pg 102, New York, Bantam Books, 1996
And as Ethan says above, "99.999%+ of what exists in our Universe is matter and not antimatter". But notice that all observed neutrinos have left handed spin in our Universe; while all observed antineutrinos have right handed spin in our Universe. So we are not only missing dark matter, dark energy, extra dimensions, we are also missing right handed neutrinos and left handed neutrinos. And other stuff.
So what I am suggesting, is that take the "99.999%+ of matter in our Universe" and the .001%- of antimatter in our Universe; and apply Hawking's (above) tranformation. Then you get a different Universe or (different subUniverse, ie extra-dimensions) in which 99.999%+ antimatter and .001% is matter but in which time is reverse. But in this different Universe or sub universe or extra-dimensions of the full UUniverse; neutrinos now ALL have right-handed spin (instead of the left-handed spin observed in our observed Universe); and also antineutrinos now ALL have left-handed spin (instead of the right-handed spin observed in our observed Universe). And of course this different subuniverse of the larger UUniverse is indistinquishable to an observer inside it from our Universe.
And thus my question (because I don't know); in this different subuniverse, via Hawkings definition, don't we also have similar tiny tantalyzing assymteries that "luck would have it, two of these criteria are very easy to satisfy" in this Hawking different universe as well as in our own visible Universe.
But this does not mean that we have, an "entirely tautological and therefore pointless" situation described. Special relativity, we know, has such tautological and apparently pointless points or view. But yes in special relativity, we can test the two points of view.
Well I say, that if we are serious about discovering extra- curled up invisible dimensions; then we had better be ready to seriously explore and think about those apparently tautological situations.
Now, I don't think I am taking Ethan's words or meaning out of context when I quote, "Why was it extra matter that was created and not extra antimatter? And when did it happen, and how did it happen?... this is one of the biggest unsolved puzzles in all of physics today."
And yet despite this being "one of the biggest unsolved puzzles in all of physics today;" Wow tells us that regarding the interpretation that I suggest and question that I ask; that "most (physicist) think it (my interpretation or question, or something along the lines of it) is entirely tautological and therefore pointless."
And it is a question because I don't pretend to have an answer; rather all I have is a testable example of a possilble interpretation, implied by that question.
Well, I agree that most physicist answer my question as nonsense, tautological and entirely pointless. But my real question is why? I mean, are not physicist trying to solve the various puzzles of our visible Universe by assuming extra-dimensions (string theory), extra- energy (dark energy), extra-matter (dark matter), and extra or dark this and that.
And yet here we have just plain old quantum mechanics and I think special relativity (not general relativity) predicting a anti-matter reverse time spin (Hawking's words above) and such a descriptive is just "tautological and pointless."
Yes, yes, I am just the village idiot; especially regarding this matter.
But I am of the strong opinion that if physics seriously wishes to move forward on ideas of extra-dimensions, extra-matter, extra-energy and so on; that in fact theorist will need to seriously consider the "tautological and pointless". And fact, theorist and experimentalist do this all the time and very well.
Of course, the ideas within "A Toy Universe" and other such amateurish papers are probably, no will most likely be show to be absolutely, incorrect science.
But off course a tautology can not be shown to be incorrect and pointless by reasoning within the current framework of concepts that lead to a tautology. Thus in this village idiots opinion; if physics and astrophysics is to find theory that explain the conundrums that lead to ideas of extra-dimensions (string theory), extra-matter (dark matter), extra-energy (dark energy) and dark this and dark that; then the correct theory (whatever it turns out to be) will have to conceptually discriminating ideas that are currently viewed as tautological and pointless and nonsense.
That is what special and general relativity did; that is what quantum mechanics did; and that in this village idiots opinion is what a new revolutionary theory in physics will need to do.
No we are not now in a revolutionary period of physics. the last 100 years of physics have been adding more bricks and mortar to the revolutionary theories of relativity and quantum mechanics.
Village idiot singing out. I of course and as always defer to the current experts on matter of detail; but I await the revolutionary experts on matters of " the biggest unsolved puzzles in all of physics today"!!!
@OKThen #25, #30: Wow did not miss your point; he just addressed it perhaps too briefly to be clear.
There are two points, one based on physics, the other based in semantics. You really do have to keep those two points clear and separate, or you are going to either get confused or give the appearance of ignorance (trust me, I've done it myself :-/ ).
First, the physics. The Sakharov conditions _guarantee_ that a matter-antimatter asymmetry will develop in any Universe in which those conditions are met. The argument (and you probably want to go back to an English translation of the original paper) is based on extremely well understood chemistry and thermodynamics, with a smattering of model-independent particle physics thrown in.
The semantics, which is what Wow addressed, are really trivial. We _define_ "matter" as "the stuff we are made of, and which we find all around us."
Suppose, hypothetically, that we lived in a universe where the K0L and K0S decayed differently than they do here. In particular, that the K0L had the two pion mode, where K0S went to three pions. In that case, the Earth, Solar System, Galaxy, etc. would be made up of what _we_ call "antiprotons", "antineutrons", and "positrons."
But in that alternate Universe, we would _call_ that stuff "matter", not "antimatter", because the latter name would just be silly. Where you attach the "anti" is purely, and entirely, a matter of convention. It is exactly the same arbitrary convention that Ben Franklin used when he got the sign of the charge carrier in lightning "wrong."
@OKThen #30: You wrote, "[...] all observed neutrinos have left handed spin in our Universe; while all observed antineutrinos have right handed spin in our Universe. So we are not only missing dark matter, dark energy, extra dimensions, we are also missing right handed neutrinos and left handed neutrinos. And other stuff."
It's not a matter of "missing" them. The weak interaction, which is how neutrinos are created and destroyed (recall the ladder operators of your first-year quantum course), is maximally parity violating. It *ONLY* touches left-handed neutrinos, or right-handed antineutrinos.
The weak interaction is one piece of a very nicely "complete" structure which covers every particle interaction we have ever encountered -- the Standard Model, despite its superficial flaws, is both mathematically and experimentally complete. Every particle predicted from its symmetry groups has been observed, and every observed particle fits into those symmetry groups.
If you want to find something you'd call a "right-handed neutrino", you need a whole new superstructure, in parallel to the SM. You can't just "tack them on" and maintain the mathematics and physics we have now. Supersymmetry is one such superstructure, but up to now its predictions have not been confirmed in any way.
@#22 Wow QUOTE:- "...the production and the detection of such things do not include the effects of some force that keeps them apart and yet they’ve not yet found any evidence in all those events of such a force. Either it’s so impotent it doesn’t appear above the noise level (and the discernment of these apparati are high indeed), or it doesn’t exist. It’s a bit like if quantum tunneling was incorrect. Experiments on it may not be too common, but the effects of it AS IS are used, therefore any change to how it works would have been noticed in the items we use that rely on it."
Thanks for the part of your answer I've quoted above, but I don't understand why are you telling me...
What is the connection to my comment?
@#29 qbsmd QUOTE:- "How is the left or right side of a muon or other particle defined? I get that spin is one axis (drawn as vertical). But what defines forward, backward, left and right?"
This is what Morton Tavel, a prof. of physics wrote:- "When certain elementary particles move through a magnetic field, they are deflected in a manner that suggests they have the properties of little magnets. In the classical world, a charged, spinning object has magnetic properties that are very much like those exhibited by these elementary particles. Physicists love analogies, so they described the elementary particles too in terms of their 'spin'
Unfortunately, the analogy breaks down, and we have come to realize that it is misleading to conjure up an image of the electron as a small spinning object. Instead we have learned simply to accept the observed fact that the electron is deflected by magnetic fields. If one insists on the image of a spinning object, then real paradoxes arise; unlike a tossed softball, for instance, the spin of an electron never changes, and it has only two possible orientations. In addition, the very notion that electrons and protons are solid 'objects' that can 'rotate' in space is itself difficult to sustain, given what we know about the rules of quantum mechanics. The term 'spin,' however, still remains"
"Thanks for the part of your answer I’ve quoted above, but I don’t understand why are you telling me…
What is the connection to my comment?"
I was responding to the idea that there is some mystical force keeping matter and antimatter apart and that if this existed to any meaningful degree, it would have been observed in the processes already taken.
"Then you get a different Universe or (different subUniverse, ie extra-dimensions) in which 99.999%+ antimatter and .001% is matter but in which time is reverse."
If that's your scenario, OKThen, then I did miss it.
However, that universe would be either indistinguishable from our own, since an antiparticle is a particle moving in the opposite direction, or unphysical where cause is the result of the effect of that cause. Since we define time as "the direction where that doesn't happen" (crudely, but in the modern definition, that's what we're doing), that is not possible.
Michael Kelsey @31 and @32
Thank you very much. This is exactly what I did not understand.
I will have to do some follow up study upon the ideas that you touched upon. Particularly, " K0L and K0S decay" and "The weak interaction, which is how neutrinos are created and destroyed (recall the ladder operators of your first-year quantum course), is maximally parity violating. It *ONLY* touches left-handed neutrinos, or right-handed antineutrinos."
I did not know that neutrinos were "maximally parity violating". I did not know that there was such a concept.
Specifically, ALSO, I did not know that "If you want to find something you’d call a “right-handed neutrino”, you need a whole new superstructure, in parallel to the SM." Ouch, ouch!
So the Standard Model of particles can't even accommodate the something called a "right-handed neutrino". Thus when a paper like this Quantum Entanglement on Cosmological Scale, A. Nicolaidis and V. Kiosses, 2012, http://arxiv.org/pdf/1211.0356v1.pdf. (which is a serious speculative paper); discusses this possibility; it is implicitly changing or going beyond the Standard Model. I did not know this.
Here's a quote from that paper, pg 7 "Within our approach the left-right symmetry is achieved with the extra dimension hosting two “mirror” branes, a left-handed brane and a right-handed brane.. From a phenomenological point of view the particles living in the “other” brane behave as mirror-duplicate of the particles in our visible world. The most prominent candidate for mediation between the two branes is the neutrino particle. The left-handed neutrino, an essential ingredient of the standard model, resides in our brane, while its counterpart, the right-handed neutrino, resides in the other brane."
I just found this paper, which is interesting and speculative, and most likely quite worthy. It is a paper that has many paragraphs that are readable and convincing to me; however I defer to experts (such as Michael Kelsey) to decide upon the merit of the science theory this and other papers suggest.
And let me add a few words about why I so willingly defer to experts. First, I NEED a clear explanation that I can understand and that makes sense to me. Once I have that, then if my imaginative idea no longer has strong enough legs (in my opinion) to stand upon; then if I am science minded, I must defer to the experts; or else, I was being dishonest in asking for an explanation in the first place.
Next, when I then search and find a serious (yes speculative) paper that in some small way agrees with my ideas (yes stated much better and more carefully than mine); but is clearly beyond my capability to evaluate. Well then again and I still must defer to the experts. I am very glad that the experts are considering such a paper. But I can't evaluate it or vote for it. Science is not a popular election; the only folks whose opinions matter are those whose knowledge is sufficient to consider and argue the merits or not of a paper (like the above mentioned paper) IN THE DETAIL. Because it is in the detail that a science theory must be correct.
So I will watch and learn. The experts must argue the merit or not of their idea. Just as I as an amateur have argued as best I could the merit of my idea. And once Michael Kelsey has been generous with his time and pointed out the error of my thinking. Well unless I have a better idea (and I don't); I have to say, "thank you for that education."
@MichaelKelsey re #32, off topic: "...the Standard Model, despite its superficial flaws, is both mathematically and experimentally complete..." I don't think it is. See what Michael Fisher said in comment #34. Look at the Einstein-de Haas effect. Spin is real, and yet there is no electron model in the Standard Model. I think the Standard Model is like the scaffolding you put up when you're building a house. It's complete in itself, but it's still full of huge gaps. People have tried to put superstructures on top, but they've been blown away like bamboo scaffolding that isn't tied in. Rightfully so IMHO, because if you don't really understand the electron, there isn't much point proposing a selectron. To bring it home, see this. Photons do not spend their lives magically transforming into electrons and positrons, which then magically transform back into one photon which nevertheless manages to keep on propagating at c. Virtual particles are virtual, light bends itself into an arc, there's a photon-photon interaction, but it just doesn't feature in the Standard Model. I think there's loads of work to do yet, and that saying the Standard Model is complete is like turkeys voting for Christmas
"Spin is real"
But not the same thing as on the macro scale, John.
@Wow. Please read me at #17
I still don’t understand why you're saying what you say in the second half of #22, and when I ask you to explain further you reply at #35 with this:- "I was responding to the idea that there is some mystical force keeping matter and antimatter apart and that if this existed to any meaningful degree, it would have been observed in the processes already taken"
I can't see where I've invoked or alluded to a "mystical force keeping matter & antimatter apart." Are you talking about my comment about how to contain pellets of antimatter for future use as fuel? If so, what is wrong with what I've written? It's my understanding that's it's difficult to contain uncharged pellets of antimatter [if we could make them] so that it doesn't touch matter & it seems sensible to make it magnetic by supercooling it [assuming the particular antimatter is of a type that enters the necessary thermodynamic phase with ease at a reasonably high temp.].
What am I missing in my understanding or are you answering someone else or are you over-explaining? I'm completely flummoxed by your responses. :)
"@Wow. Please read me at #17"
Why? I believe I've already read it, so what am I supposed to be looking for?
"I still don’t understand why you’re saying what you say in the second half of #22"
Fair enough, don't understand it. no skin of my nose. I have no idea how to rephrase it to get it in a form you can comprehend and, frankly, can't give a rats' ass.
@Wow re #39: it is the same thing as on the macro scale.
Check out the Einstein-de Haas effect which "demonstrates that spin angular momentum is indeed of the same nature as the angular momentum of rotating bodies as conceived in classical mechanics". The electron isn't some spinning point-particle though. It has a wave nature. And see Dirac's belt, it's a spin ½ particle, the wave path is like tracing round a moebius strip. The rotation is biaxial and tuned so the result is a standing-wave "structure". Hence in atomic orbitals electrons "exist as standing waves". You can diffract electrons, they definitely have a wave nature, and they have a magnetic moment. Think of something like the spindle-sphere torus on Adrian Rossiter's antiprism website, but without any surface because they're "just field". Or wavefunction or whatever you prefer.
The trouble is that this just isn't in the standard model, which simple says the electron is a fundamental particle, even though you can create them and destroy them along with positrons in pair production and annihilation. For an analogy think of a hurricane. Take away the rotation and all you've got is wind. Take the rotation away from an electron and all you've got is light.
Yes the experts are incorrect and misunderstand the deep dark detail of physical reality. But does that mean that you understand the deep dark detail of physical reality better than the experts? Ouch, ouch! Time for a group cry.
Oh! Well? Yes, you are still entitled to your crazy hunches. Of course, only until you are shown the flaw in your reasoning. Ouch, ouch! Time for another group cry.
But you deny the experts' excellent clear reasoning. "I can't hear you; I can't hear you; I'M NOT LISTENING. Jabberwocky, jaberwocky." Well then, you don't have to say Ouch and cry. Brilliant!
But even then, it is good to clearly say whatever it is you are trying to say; or else, how is another village idiot like me to be able to agree with you in my own words?
Ahh, brillant. I repeat exactly the words you say. "Check out the Einstein-de Hass effect.. see Dirac's belt.. think of a spindle-sphere torus.. or whatever you prefer.. and.. you've got light." It doesn't matter that I have no idea what you are talking about; I can repeat the mantra.
But this village idiot does not repeat mantras. I like to consistently misunderstand in my own words.
#41 Wow. You make it your business to pick up on the errors of others & so you should be more gracious when further explanation is requested ~ or don't bother correcting others to begin with.
I'm assuming you're capable of a classier response than the immaturity you've just exhibited, but you can't respond with anything better because you don't have an answer. You just misread my original question & went into lecture mode.
#44 Michael Fisher
Wow #22 answered your original question #17 quite well.
Whereas you Michael Fisher, comments #33, #40 and #44 seem determined to provoke and annoy Wow.
Thus, Wow #41 response to you seems quite restrained and civil.
Here's a question for you Michael Fisher, How much anti-matter would you consider "a lot"? I mean if you are arguing about Wow's definition of "a lot"; you must have an idea of what you consider "a lot." This village idiot is waiting anxiously your answer. I can't wait. I can't wait.
I have always wanted to know what "a lot" was. Have you conducted a survey? How have you come to your conclusion?
@ #45 OKThen. Wow's reply at #22 to my query about what's "a lot?" was fine & I've mentioned it no further in this thread.
Then Wow goes on to write in the same reply:- "The production and the detection of such things do not include the effects of some force that keeps them apart and yet they’ve not yet found any evidence in all those events of such a force.
Either it’s so impotent it doesn’t appear above the noise level (and the discernment of these apparati are high indeed), or it doesn’t exist.
It’s a bit like if quantum tunneling was incorrect. Experiments on it may not be too common, but the effects of it AS IS are used, therefore any change to how it works would have been noticed in the items we use that rely on it"
I have no idea how that part of his/her reply is related to my question & so I asked what the connection was [I'm genuinely curious to understand what I've missed] & Wow replies thus:- "I was responding to the idea that there is some mystical force keeping matter and antimatter apart and that if this existed to any meaningful degree, it would have been observed in the processes already taken."
I'm now completely confused because I haven't assumed there is a "mystical force keeping matter & antimatter apart" in any part of my original #17.
I still don't understand what Wow is getting at & I'm driven to conclude it has something to do with what I've written in #17 under the section labelled "QUESTIONS FOR ANYBODY", but I can't see what it could be
I'm not attacking Wow ~ I'm trying to understand Wow's thinking on a subject about which I know little & where is it that Wow thinks I've invoked "mystical forces"
#46 Michael Fisher
Also, many of my questions (on this blog) do not get answered.
Why will someone not answer my sincere questions?
Maybe they don't know an answer, maybe their best answer is NOT to answer, maybe they think my question is nonsense, maybe they are busy about things more important to them. All are perfectly acceptable civil answers.
As for "trying to understand Wow's thinking on a subject"; or anyone's thinking upon a subject; it is best to first try to clearly understand my own thinking upon that subject even if I "know little."
The internet, books are our teachers that do not scold. Yes more than even our classroom teachers and internet acquaintances. Because after all, the important question that I (or you) wish to have answered is our own. We know that question. And if we know how to read and how to use the internet; then we can search (not to know someone else's answer) but to deepen our own understanding; to better frame our own question if not answer it (to our satisfaction).
Of course the process of learning is not for the lazy; it is for the leisurely. Lazy means I want the perfect correct answer without any personal, intellectual, or emotional effort. Leisurely means that I am willing to invest great personal, intellectual and emotional effort into my question because I am curious.
Those who confuse leisurely with lazy, have mistaken lie-surely with leisurely.
Notice that leisurely inquiry is very different from lazy inquiry (e.g. have you heard any celebrity scandals) and from practical inquiry (e.g. who could shovel my snow). Leisurely inquiry is intense curiosity driven inquiry to know ourself and the world. Leisurely inquiry requires even more than intense curiosity, intense self integrity and self honesty (we can not lie to ourself). Yes in my mind, the liberal arts (e.g. much of philosophy, science, mathematics, and arts) are about leisurely inquiry.
So does it matter if Wow or others out here ignore our questions? Notice that I have ignored your questions; but not with malice.
" it is best to first try to clearly understand my own thinking upon that subject"
QFT.
"@Wow re #39: it is the same thing as on the macro scale. "
No it isn't.
Because if it were matter spinning around, then the surface of the electron would have to be moving faster than the speed of light to produce enough momentum to produce that level of spin energy.
John, your problem appears to be that you think everyone else a moron.
Projection is the only cause for this malady of yours.
"John, your problem appears to be that you think everyone else a moron.
Projection is the only cause for this malady of yours."
Did you really write that Wow, or has sombody else posted using your alias? Priceless if you did!
Not even for a second suggesting might have a point, but perhaps you coulds elaborate on this please:
"Because if it were matter spinning around, then the surface of the electron would have to be moving faster than the speed of light to produce enough momentum to produce that level of spin energy."
Did you mean to say "Because if it were the rest mass of a homogeneous sphere spinning around, then..." ? Is there any reason the rest mass of an electron cannot be due to the relatavistic masses of its constituents, or constituents constituents, spinning about each other (whether or not we have any knowledge of the source of the forces to do that.)
I meant what I said, Dai.
And obviously you're a pauper by what you consider to be priceless, dear.
Wow, you really should try showing a bit more empathy with the lesser mortals around you who have to go through life constantly encumbered by a nagging doubt that they might occasionally be wrong about something.
Dai,
Please stop pretending you know me just so you can make up some monstrous strawman to attack.
It's pathetically obvious.
I treat you with all due respect, Dai.
Just because you deserve none does not mean you're like everyone else on the internet, dear.
@Michael Kelsey, haven't seen an reply to your comment.
I would want to know what observations show that there are not an equal number of matter and anti-matter galaxy clusters. That would solve the supposed M / AM imbalance. The only problem is there should then be radiation where the surrounding gas clouds collide. But this would be minimal if the gas density between clusters is very low. Maybe some of the mysterious high-energy signals are from M/AM star collisions?
Yes, I see why David L defends John Duffield against the scientific sensibility of Wow.
"The electron is a trivial knot, a turn and a twist. The proton is a trefoil knot, three turns and a twist.. this photon is tied in a 511 keV knot.. It tells you how fast the energy, that is going nowhere fast, is going somewhere.. The photon's got no mass. But all you need to do is tie it in a knot and now it does." quotes by John Duffield from his book on amazon.
And I thought that I was the village idiot!!!
Yes, I see why David L defends John Duffield .......
Really? What a perceptive person you must be! I have not even expressed an opinion on John Duffield, I had never even heard of him before today. Hell I haven't even read his post, let alone his book. I simply asked Wow to elaborate on his comment in response to John .
.........against the scientific sensibility of Wow.
You are entitled to your assessment of Wow, but I'm still reserving judgement. His debating style is rather like a Gish Gallop without the manners. He seems to prefer to resort to semantic Python-esque arguments rather than discuss the central issue under debate. This may be because he is miles more knowledgeable than all the other posters here, with no patience to address the piddling questions of lesser men, and that a "moron" by definition is anybody less knowledgeable than he. Or it may be because he is a classic example of the Dunning-Krugger effect for whom a "moron" by definition is anybody who disagrees with him, and detailed discussions expose him to the risk having to face the gaps in his knowledge of what he posts about. I like to keep an open mind on these things until I have evidence upon which to judge.
Well then David L, enough said about Wow's response #39 to John's response #38 (i.e. John Duffield); which Wow commented on #49, and which you (i.e. David L #50 ) then commented upon.
Pardon my assumption that you were following the thread.
And good for you for not defending John Duffield.
And good for you for reserving judgement on Wow.
Wow sometimes is a bit crotchety with no tolerance for nonsense, scientific or otherwise. But he is scientifically fair minded and I find it best to ponder Wow's words, even (maybe especially) when I disagree with him.
The other day, I was enjoying a quiet walk in the park when three dogs of pedigree ran growling towards me. I spread my arms, smiled like a madman and hurried forward to embrace then. Alas dogs being dogs, they had nothing more to say as they scurried back to their master.
I like Wow best when he is his own master, insightful and educating about the science that he understands so well; rather than when his is growling back at other dogs real or imagined.
@Gary S #55: Hi, Gary. When I wrote up a public lecture on CP violation back in 2006, the best reference I could find was a 1996 CERN report. It used a "distance ladder" approach, which I sort of outlined in my previous comment.
It reported a limit of AM/M < 10^-7 out to 20 Mpc, based on the lack of observed _large-scale_ gamma emissions (which is what you'd expect, just as you described, from contacts between galaxy cluster haloes).
I'm not an astrophysicist, so I don't see how you can use the distance ladder to get beyond galaxy clusters. Superclusters are separated by voids with a density far below the average inter-galactic medium (IGM). To my naive eye, that means you can't get a decent limit on broad-area gamma emission at those scales, because the expected flux would be too low (not enough stuff there).
I posted my comment because I'm not an astrophysicist, and I hoped that Ethan might know about more recent results (my quick Google Scholar search didn't pan out). Unfortunately, it probably got lost in the sturm und drang :-(
@OKThen #37: Here is a brief, jargon-filled outline. This is meant to give you the right keywords to drive a search for more complete information :-)
The K0L/K0S system (the long-lived and short-lived neutral K mesons) is where CP violation was first discovered in 1964. The K0 and anti-K0 mesons are the "mass eigenstates" with definite quark content (anti-s d and s anti-d, respectively).
The K0 and anti-K0 are each different superpositions of the weak-decay eigenstates K0L and K0S, which "ought" to have opposite parity and CP. In particular, the K0S decays to two pions (pi+ pi- or pi0 pi0), while K0L decays to three pions (pi+ pi- pi0 or pi0 pi0 pi0). Those decay final states have opposite CP. But it turns out that a few per mil of K0L decay to two pions, which would be forbidden if CP were exactly conserved.
"Yes, I see why David L defends John Duffield against the scientific sensibility of Wow. "
It isnt really support of John that Dai is doing.
It's destruction of Wow he's wishing to accomplish.
#60 Michael Kelsey
Sometimes when searching to learn; it takes a while to realize that we are searching upon the wrong words and ideas because we don't know the correct jargon or language of the specialist.
Thanks again.
"It’s destruction of Wow he’s wishing to accomplish."
Paranoia too? Rest assured I have no reason to rate your destruction any higher on my list of priorities than the destruction of any of the other 7 billion souls on Earth. However, I am beginning to think that should it become an ambition I can rely on your help.
@Wow re #49: It is. The Einstein-de Haas effect proves it.
But it isn't matter spinning around. Matter is light spinning round and round, hence E=mc². You make an electron in pair production out of light. You destroy it in annihilation and you've got the light back. In between you've got the Einstein-de Haas effect and magnetic dipole moment and electron diffraction and the wave nature of matter. Duh! Matter *is* light spinning round and round. A radiating body loses mass. In electron-positron annihilation the radiating bodies lose all of it, and then they aren't there any more.
The electron isn't matter spinning round. It has no surface. Field is what it is. There is no surface spinning round faster than light. What a straw man that is, what a canard. It's just light going round thataway at c whilst twisting thisaway at half that rate as per the Dirac's belt Moebius strip. Then inflate it because it isn't a strip or a hoop, because there's no electric dipole moment. Go look at that spindle sphere, appreciate that a sphere is associated with a 4π solid angle then divide 4π by c to the power 1½. Don't worry about the dimensionality or the binding energy. Then work out c to the power ½ divided by 3π.
It's all simple stuff. What's not to like? But hey, if you'd rather believe in myth and magic, that's up to you.
David: apologies, there are some ignorant naysayers on this website along with their fawning groupies. Best not to pay too much attention to them, Best to stick to the physics and the hard scientific evidence.
Except, John, you are not the one with the correct interpretations.
John Duffield
Please follow me to Ethan's page
http://scienceblogs.com/startswithabang/2012/09/23/weekend-diversion-yo…
where I we can continue this discussion in an appropriate place.