"There are things known and there are things unknown, and in between are the doors of perception." -Aldous Huxley
From tiny, laser-light wavelengths to dark skies to dark matter on the largest scales in the Universe, it's been quite a week at the main Starts With A Bang collection over at Medium. New this week, we've talked about:
- Is there a limit to Lasers? (for our Ask Ethan series),
- Finding darkness (for our Weekend Diversion),
- The globular cluster Messier 4 (for Messier Monday),
- The Unparalleled Power of Experiment,
- The Death of Dark Matter's #1 Competitor, and
- The Whole Story on Dark Matter (for Throwback Thursday).
As always, you've come over here and had your say, both to me and to one another, in the comments section. Each week (and we're in the double digits now), I've been highlighting -- and responding in great detail -- to my favorite Comments of the Week in our new series here, so let's get right to it!
Image credit: © 1998-2013 by Michael W. Davidson and The Florida State University, retrieved from http://micro.magnet.fsu.edu/primer/java/lasers/heliumneonlaser/.
From Odi on the topic of a limit to a laser's energy: "In the Update at the end you say that photon energy was a limit factor. But a laser doesn’t increase photo energy (hv) at all, only intensity."
This is true; in fact, both of these things are true! It just isn't necessarily intuitive as to how, so let's see if we can clear things up. When you produce laser light/energy, you're producing photons of a very particular and fixed frequency (ν, which is a Greek "nu", not a Latin v), which can range in wavelength from very long radio waves to incredibly short gamma-rays. But when we talk about intensifying the power of a laser, you are correct; we are typically turning up the number of photons, not turning up the individual photon energy. For practical lasers, there's a limit to the number of photons the cavity can support, but in principle that number is not limited at all, and we've been able to increase that number with no limit in sight.
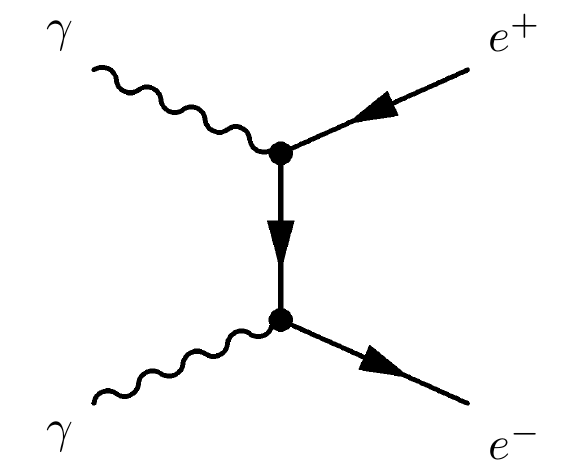Image credit: Tanmoy Laskar of Astrobites, via http://astrobites.org/2011/05/21/when-photons-talk-to-each-other/.
But how, then, would we get up to energies required to produce particle-antiparticle pairs? As it turns out, if the density of even low-energy photons is high enough, they can interact with one another through the electromagnetic force to produce a small number of higher-energy photons, a nonlinear effect that requires either a "shitload" or "asston" of photons, depending on which technical term (or which physicist) you prefer.
Image credit: Wikimedia Commons user Stannered.
The photon-photon interaction cross-section is very small, and gets smaller as we go to lower and lower energies, but we've managed to achieve number densities so high that quantum electrodynamic effects have actually been observed! So the total energy of the system is conserved, but higher-energy photon states can legitimately be achieved, high enough to produce particle-antiparticle pairs from lower-energy photons that couldn't on their own!
Image credit: Google Earth with Light Pollution Overlay.
From D. C. Sessions on the topic of light pollution and dark skies: "Tough assignment. Right now I’m in Socorro NM, half an hour from the VLA on the Plains of San Augustin. From the front yard I can see Magdalena Ridge Observatory. At night, walking a couple of blocks from the brewpub at the Plaza to home, I can look up and see the Milky Way. Small towns in States that take dark skies seriously. Eat your hearts out."
It's easy to laud the dark sky initiatives that some states like Arizona and New Mexico have taken, but let's not kid ourselves. At least in the United States, there's pretty much a 1-to-1 correspondence between population density and light pollution. You've seen the map of light pollution, above, now check out population density, below.
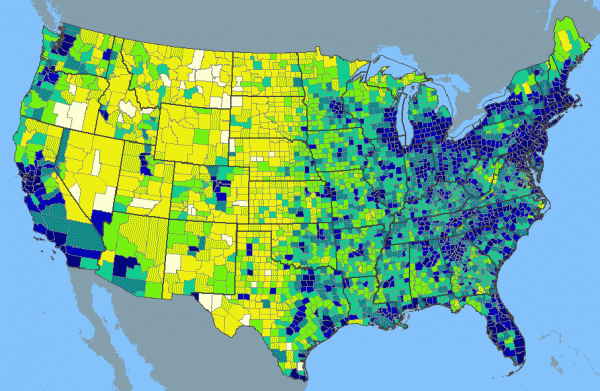Image credit: National Atlas of the United States, via UNC Chapel Hill at http://www.learnnc.org/lp/multimedia/14566.
Yes, it's true that cities like Tucson and Albuquerque are doing a better job than most when it comes to mitigating light pollution, but it's not like they're doing a very good job objectively. They're doing something rather than nothing, but we're a long way from having dark skies inside of a large city anywhere in this country. It's merely the case that it's a lot easier to reach a location where virtually nobody lives in the western half of the USA than the eastern half. We would all benefit from doing a lot better on this front.
Image credit: Thomas Reisinger. Created using GNUPlot, under c.c.a.-sharealike-3.0.
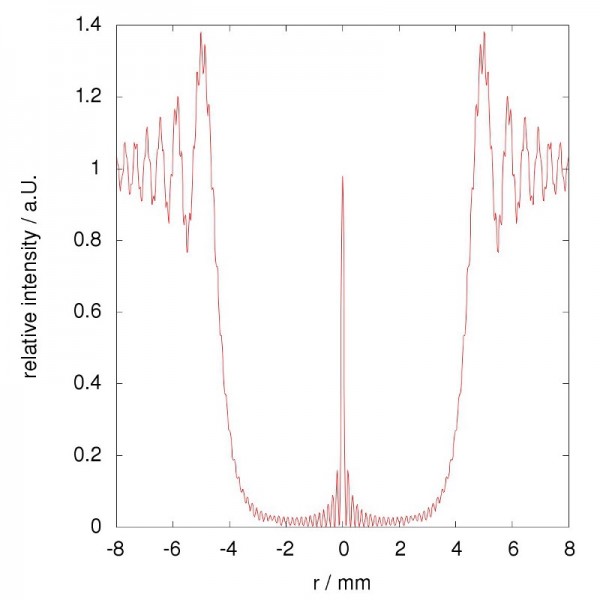
From Mark McA on the topic of the unparalleled power of experiment: "What a cool story! Can you explain more about the intensity chart? I was wondering a few things:
1) Does it actually touch zero at any point, or does everywhere have at least a tiny probability of getting a photon?
2) What are the steps on the curves – and why no steps for the smooth curves either side of the spot?
3) What’s the pair of ‘squashed wave’ anomalies at +/- 2.5?"
Three questions? Well, let's just do it. This is a simulation of an actual setup, where you have a coherent light source -- light of a finite, fixed wavelength -- spreading out from a point at a specific (narrow) angle, passing around a theoretically perfect sphere of finite size (4 mm, in this case) a certain distance away, and then displayed on a screen another fixed distance away.
Image credit: Auburn University.
I'm warning you now that the answers will go from most interesting to least interesting:
1.) In real life, because the wavelength of the light is finite and the sphere is only likely to be perfectly spherical to a few Ångstroms' accuracy (after all, the sphere is still made of atoms), no, it will never truly touch "zero" intensity. Although, in the limit of a perfectly spherical (to arbitrary accuracy) sphere, you will get perfectly destructive interference at the absolute minima.
2.) For this particular configuration, there are seven dark-bright-dark cycles per mm as seen on the screen. The "steps" you see on the upswing of the curve around the ±4 mm mark are caused merely by that same wave pattern; there are none on the central peak because that peak is just one cycle across!
3.) Those are due to imperfections of 10 µm in size that have been superimposed on the sphere in this simulation. Otherwise, the "squashed anomaly" would disappear, and the intensity would merely be a smoothly-rising curve with the square of a Bessel-function superimposed on top. (See here.)
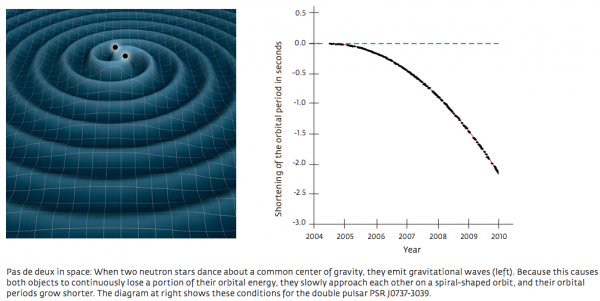Image credit: NASA (L), Max Planck Institute for Radio Astronomy / Michael Kramer, via http://www.mpg.de/7644757/W002_Physics-Astronomy_048-055.pdf.
From Steve Carlip on the Death of Dark Matter's #1 Alternative: "It would be helpful if you included a citation to a refereed paper with this claim. The closest I’ve found by any of the authors you refer to is Freire et al., Monthly Notices of the Royal Astronomical Society 423 (2012) 3328–3343. But that paper concludes, “Therefore, the results of the present paper do not rule out TeVeS, but show that its original 2004 formulation by Bekenstein may need to be amended. At present, even its original writing is consistent, although it does need some tuning.” Is there something more recent? Where? (I’m not defending TeVeS here, but if there’s really a new result I’d like to know the details.)"
The results that Steve Carlip -- who's an excellent scientist specializing in General Relativity, for those who don't know -- refers to in Friere et al. are perhaps the most recent that are published, but that same team has a draft in preparation that they claim is good enough to falsify all physically interesting incarnations of TeVeS using improved measurements of that binary pulsar system. There is a link to a slide deck that has their latest results (or at least, what they're presenting publicly) here. Here are three relevant slides:
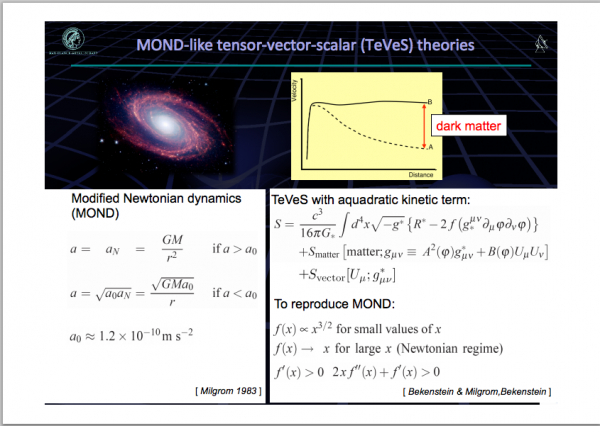Image credit: Michael Kramer, via http://www.astro.uni-bonn.de/NS2013/Kramer_Double_Pulsar.pdf.
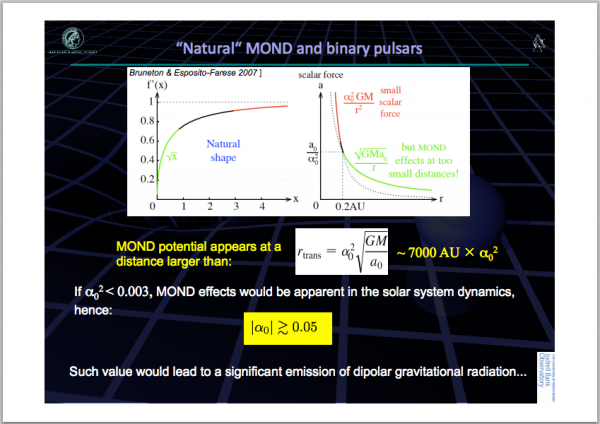Image credit: Michael Kramer, via http://www.astro.uni-bonn.de/NS2013/Kramer_Double_Pulsar.pdf.
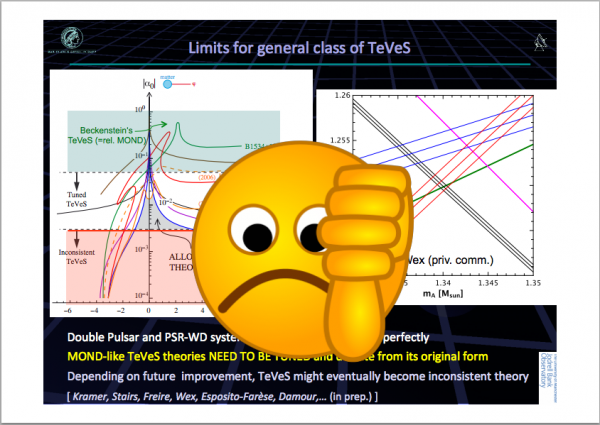Image credit: Michael Kramer, via http://www.astro.uni-bonn.de/NS2013/Kramer_Double_Pulsar.pdf.
Interestingly enough, there's also a review paper by Wex -- the one whom I quoted as stating "In our view, this refutes TeVeS" -- that talks about the improved constraints that can be learned by studying binary pulsars on theories that differ from GR. For those of you who've heard of Brans-Dicke gravity (that was a scalar-tensor theory of gravity), there's a parameter () that was initially proposed to be around five, but as it goes to infinity, it reduces to standard GR. Back when I was in grad school about 12 years ago, it was constrained to be bigger than around 10,000 from Solar System observations; it looks like using binary pulsars that constraint is now bigger than 300,000,000!
I also received an interesting follow-up from Steve Carlip (privately) that I wanted to share with you:
I'm a bit leery -- TeVeS-like theories are awfully resilient. One standard escape hatch is the Vainshtein mechanism, which I think is very poorly understood in general, but which sometimes allows a theory that looks as if it ought to be very different from GR to mimic GR at short distances. This gives you a lot of room to screw around with the long distance behavior.
For those who want to learn about the Vainshtein mechanism, there's a good recent (but technical) review here.
Image credit: NASA / Goddard Space Flight Center / WMAP101087.
And finally, from Jim Sky on the same topic: "How do we know that dark matter is definitely not baryonic? I missed that."
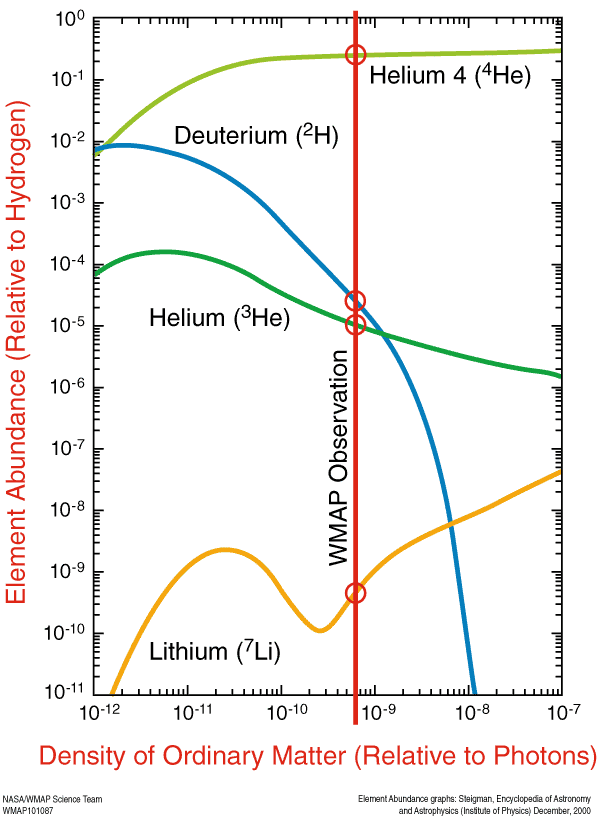
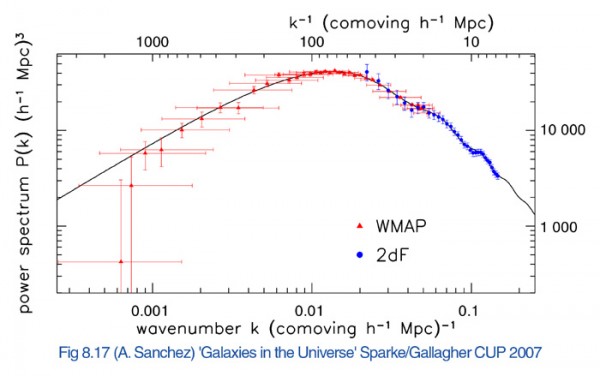
This was a good enough question that when I saw it, it went and inspired me to do this week's Throwback Thursday on exactly that topic, and more. But in brief, it's that we know how baryonic matter interacts with photons, and those results show up in the primordial abundances of the light elements (above), the pattern of fluctuations in the cosmic microwave background, and the magnitude of the "wiggles" in the large-scale structure of the Universe's power spectrum (below). These are three different sets of measurements that can all measure the overall energy density of baryons in the Universe, and the latter two data sets can also measure non-baryonic dark matter.
Image credit: A. Sanchez, Sparke/Gallagher CUP 2007.
All three of these sets of observations point to a Universe where the total baryon density is around 4.5-5.0% of the critical density, but the latter two show a dark matter density of around 23-29% of critical density. So those three independent measurements of the light elements, the cosmic microwave background, and the large-scale structure of the Universe -- or if you like acronyms, BBN, CMB and LSS -- all teach us that the vast majority of dark matter is most definitively non-baryonic.
And that's all for this edition of Comments of the Week!
- Log in to post comments