Comments of the Week #30: From Mars to Aliens and Beyond

“The important thing is not to stop questioning. Curiosity has its own reason for existing.” -Albert Einstein

After a wide-ranging week here on Starts With A Bang, it's only fair to take a look at what conversations this has sparked among all of you, and to jump in where there's a good opportunity to add even more amazing stories about the Universe into the mix. In case you missed anything, this past week saw us cover the following topics:

• Could a manned mission to Mars abort? (for Ask Ethan),
• The ultimate fighter... of stains? (for our Weekend Diversion),
• The most elusive globular cluster, M55 (for Messier Monday),
• The strangest theory we know is true (by contributing writer Brian Koberlein),
• CMB part 1: the "smoking gun" of the Big Bang (by contributor Amanda Yoho),
• Preparing for Alien Life, and
• How big is our observable Universe? (for Throwback Thursday).

You've had a lot to say, particularly about Mars, Relativity, Alien Life and the Observable Universe, so let's dive on in to the latest edition of your Comments of the Week!

Image credit: Inspiration Mars Foundation.

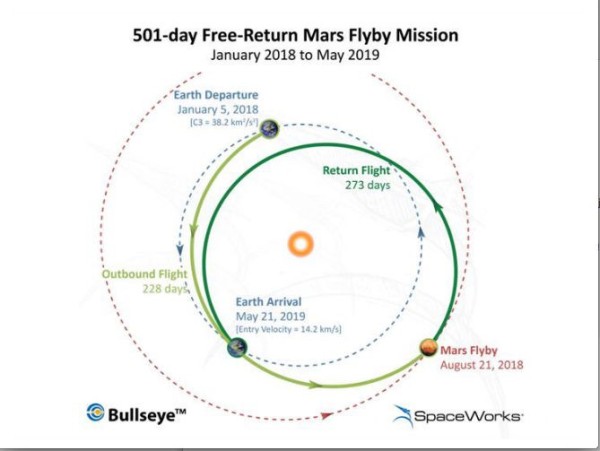
From Michael Kelsey on the subject of traveling to Mars: "I wish I knew more celestial mechanics! Is it really the case that the Hohmann transfer orbit tracks the departure planet? Your diagram shows a “Mars flyby” where the return path meets up directly with Earth’s position at that time. Does that flyby involve a change in velocity, or just (effectively) no hitting Mars?"

Imagine you've got two perfectly circular orbits around the Sun, where one orbit is farther out than the other. This could be representative of Earth and Mars, for example, or of Earth and Venus, if we wanted to consider ourselves as the outer planet. The inner orbit has a total amount of energy that's less than the outer orbit; in other words, we'd need to boost to a greater speed to reach it, while if we were the outer orbit, we'd need to strip some of our speed away. The idea of a Hohmann transfer orbit is that, while you're in the orbit of the inner (or outer) planet, you change your velocity so that your orbit becomes very elliptical! When you reach perihelion (or aphelion) in your orbit, you'll intersect with the orbit of your original planet, but when you reach aphelion (or perihelion), you'll run into the new planet, the one you were attempting to reach!

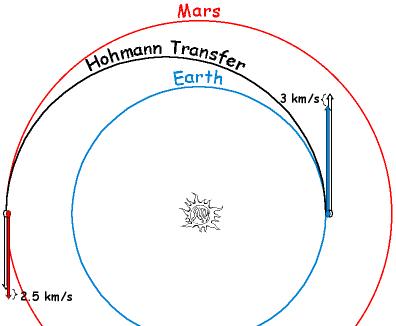Image credit: Hop David via http://clowder.net/hop/TMI/HypVel.html.

Now, timing is especially important here, because it's vital that you encounter the target planet when it's actually there in its orbit; simply intersecting with the planet's orbit if the planet isn't there is worthless! In the particular case of the flyby alluded to, you would need a gravity assist -- taking advantage of the Oberth effect -- to actually make it back to Earth when it's at the right location in its orbit. (Alternatively, you could give an additional boost, as shown above, to remain in a stable orbit with the new planet.) Still, it's possible to do a fly-by and return to the original planet with a practical amount of fuel, which is pretty amazing! That's the kind of manned mission to Mars that, with a modest budget and our present level of technology, I could easily get behind!

Image credit: John D. Norton, via http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/Special_relati….

From DavidL on the strangest theory (relativity) we know to be true: "Surely the animation shown completely mises the point.. The mirrors shown are moving in a linear fashion, distance to the observer must therfore be changing, and there must be a component of velocity to produce a doppler shift without time dilation."

The beauty of an experiment like this is that it's performed in our heads: a gedankenexperiment. If you imagine watching these two light-clocks from a distance that you can easily reach, then yes, DavidL, your concerns will be completely valid, and will influence the experiment. But we can imagine either of the following two scenarios, if it makes us feel better:

1. The light clocks are arbitrarily far away, so that the change in the distance to the observer is negligible, and so are those Doppler shifts you refer to.
2. The light clock that moves relative to you does so along a circular path centered on you, removing any Doppler shift at all.

But it's important to remember that we're attempting to capture the most important effect in the system, which is the way physics progresses. We design an experiment or test that should show a departure from the currently accepted theory, and then we figure out the primary cause of that new effect. "Completely misses the point" is a completely unfair assessment.

Image credit: Encyclopaedia Britannica.

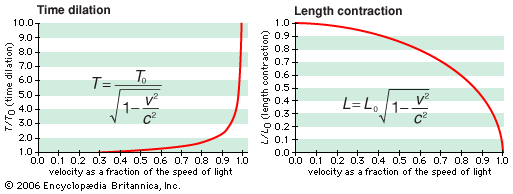
From MandoZink on the same topic: "What is possibly the strangest effect of time dilation is that a photon, traveling at C, experiences no time at all. A star’s light may have been traveling towards us for 10 billion years, but from the photon’s perspective, the instant it was emitted it was immediately detected by the observer on earth, 10 billion light years away."

This is one of the things that defies our intuition about relativity, and is also one of my personal favorite things about it. Imagine that you want to travel to a star 10 light years away. Its distance is defined as 10 light years because if something moved at the speed of light, it would take ten years to reach us. So, you reason, if you move at 0.01% the speed of light, it will take 100,000 years to get there. To an excellent approximation, this is true. If you moved there at 0.1% the speed of light, you'd think it would take just one tenth the time: 10,000 years. Again, very good. But if you moved at 1%, or 10% the speed of light, you'd start to notice slight changes. You see, it wouldn't take merely 1,000 or 100 years, but there would be some slight discrepancies between what you experienced on the spaceship and what someone here on Earth would see. Because as you move close to the speed of light, the distance that you need to travel appears to contract, and as you move closer and closer to the speed of light, the rate that time passes for you slows down as well. This results in some very strange phenomena as you get really close to the speed of light!

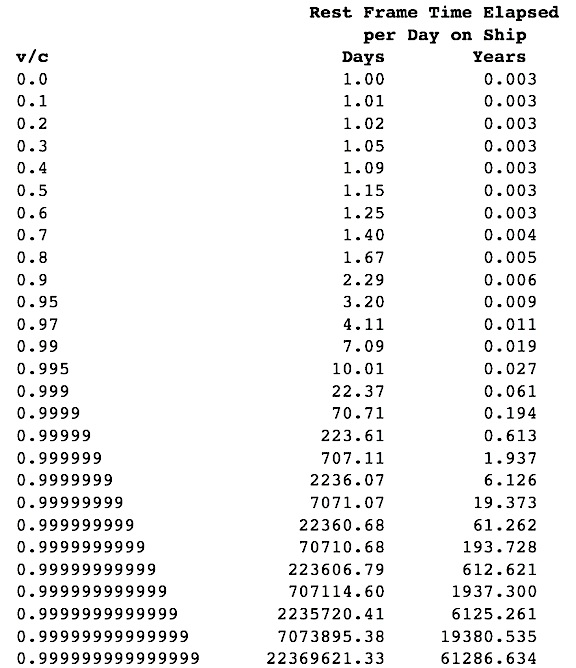Image credit: Rhawn Gabriel Joseph, via http://cosmology.com/TimeTravel1.html.

If you look at the bottom row, above, what this states is that if an object moves at 99.9999999999999% the speed of light, an external, stationary observer would need to experience more than 60,000 years in order for just a single day to pass on the ship. As you get closer and closer to the speed of light, you start to see that the Universe becomes much smaller (as distances contract), while external observers see your clock as becoming arbitrarily close to stopped. Extrapolating to a photon, or any object that moves at the speed of light (a null vector in relativity), we find that all distances contract down to zero length and all "clocks" stop completely.

If you were to ever reach the speed of light, you'd instantaneously encounter whatever it was you smashed into, or -- if you encountered nothing -- the end of the Universe, whatever that looks like.

From Michael Fisher on the topic of alien life: "Here we show that lifeless habitable zone terrestrial planets around any star type may develop oxygen-dominated atmospheres as a result of water photolysis, because the cold trap mechanism that protects H2O on Earth is ineffective when the atmospheric inventory of non-condensing gases (e.g., N2, Ar) is low. Hence the spectral features of O2 and O3 alone cannot be regarded as robust signs of extraterrestrial life..."

We have to be careful not to fool ourselves; just because the Earth is the only planet in the Solar System with large amounts of molecular oxygen, and we know that molecular oxygen is highly reactive with hydrogen or hydrocarbon (e.g., methane) gases, we often take it for granted that the only way to produce large amounts of oxygen is through biological processes. After all, molecular O2 was virtually non-existent on Earth until certain single-celled organisms starting producing it as a waste product, eventually filling our atmosphere with it.

But there are other ways to make oxygen in trace amounts: UV-photodissociation of other molecules such as CO2 or H2O could do it under the right conditions. If you contrive the right conditions -- such as an atmosphere that had virtually no non-condensing gases such as Nitrogen or Argon -- you might be able to build up significant amounts of O2 by other, abiotic means.

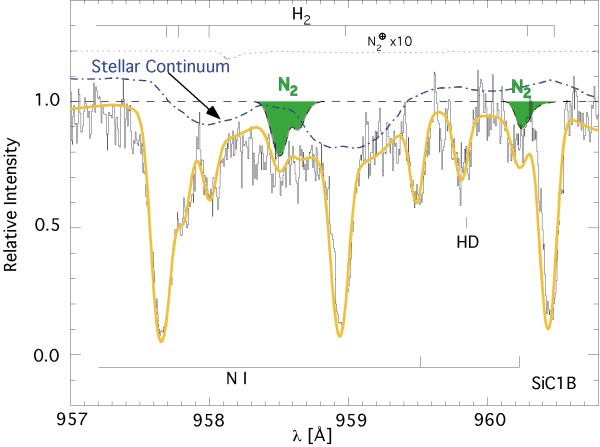Image credit: B-G. Andersson, JHU, via https://archive.stsci.edu/fuse/scisumm/sci_n2.html.

But even though Nitrogen, for example, is virtually non-reactive in the visible and infrared portions of the spectrum, it does have a characteristic UV-absorption signature, something we've seen in interstellar space for the first time just a decade ago! We want to be sure that we don't fool ourselves, but the detection of Oxygen gas around an extrasolar planet would -- and should -- set off a firestorm of research on the composition of that atmosphere.

Like I said, if we're lucky, the first signs of alien life could be a lot closer than most of us ever imagined.

Image credit: me.

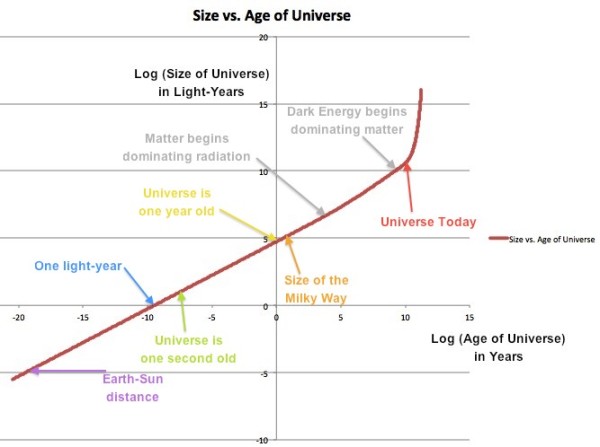
And finally, from Sinisa Lazarek on how large the observable Universe is: "Just one addition, not only how long, but also what was the size of the patch. It could have been half the size of proton, but it could have been a light year. The outcome is the same… beyond our visible, causal horizon, there can be many more of same stuff as here, or can be something different… but if inflation is correct.. it’s infinite to the future."

The fun thing about speculating about the unobservable Universe is that we know only how big our observable Universe is, and also only about the final tiny fraction of a second that our Universe underwent inflation. The known unknowns, to put it, include:

1. How much farther our unobservable Universe continues, with properties identical to the observable part.
2. How long to the past inflation existed in the region that gave rise to our own.
3. Whether inflation ended everywhere in that region the same, or whether it continues eternally in some of those regions.
4. How large the portion of the Universe that began inflating was initially, or whether inflation was truly eternal to the past.

This last portion, however, is something we can speak of intelligently. You see, whether the entire Universe began inflating together, or whether it was just a small portion of the Universe that began inflating shouldn't matter all that much. Once inflation begins in one region, that region in short order becomes arbitrarily close to 100% of the entire (unobservable) Universe!

Image credit: Frac 33 by MDK fractal of deviantART, via http://mdk-fractal.deviantart.com/art/Chaotic-Galaxies-Frac-33-94798090.

Pre-inflation, some regions might have been expanding, contracting, oscillating, filled with viscous, shearing fluid, etc. It doesn't matter. What matters is that one region, no matter how small, had the right conditions to begin inflating, and then everything else, in short order, is dwarfed by the now humongous inflation region.

Image credit: Ned Wright's cosmology tutorial.

This is why I always say that, no matter what came before inflation, inflation wipes that information out. As much as I hate to say we'll never know what came before it, we have to at least admit the possibility that, just as there's a limit to the total amount of information in our finite, observable Universe, there are likely to be some questions that the Universe doesn't provide us with enough information to answer. And this may be one of them.

Thanks for a great week of comments; let's strive to make the next one even greater!