Sunday Chess Problem

Blogging will continue to be light around here for at least another week. It's spring break, you see. That's hard to believe considering that Thursday and Friday of last week were both snow days, meaning that our spring break opened with a raging blizzard.

Spring break is a good time to make progress on various writing and research projects that inevitably take a back seat during the semester. When the students are in town, being a college professor is pretty much a standard, nine-to-five sort of job. Our days are mostly taken up with classes, preparing for classes, office hours, grading, and committee meetings. At the end of all that it is hard to find the right frame of mind for scholarly pursuits. And since research typically entails long bouts of staring at the wall getting nowhere, it is also hard to find enough time to make progress.

People often get down on college professors, and teachers more generally, for all the time we allegedly get off. We are often charged with only working nine months out of the year, for example. Those who make that criticism have no idea what they are talking about. These are folks who think that teachers are only working when they are facing students in a classroom. The reality is that summer break, for example, is often a time when we work harder than during the regular semester.

That said, it is important to have one's priorities in order, and Sunday Chess Problem is definitely one of those priorities! So I have something a bit unusual for you this week. The following problem was composed by Norman Macleod in 1977. The stipulation calls for mate in two, but there is a big catch. We are playing this game under Circe rules!

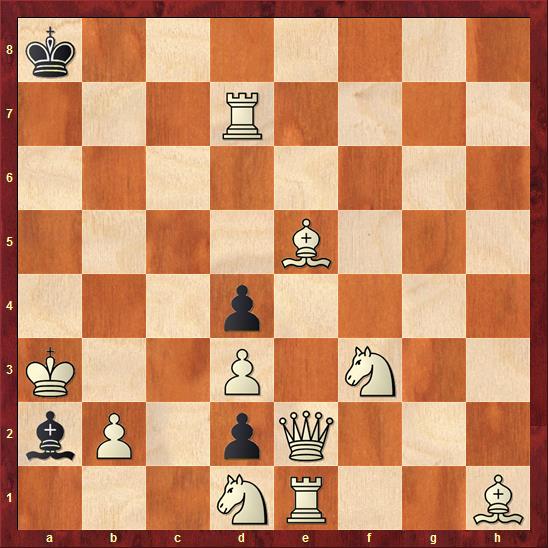
This takes a bit of explaining. In Circe chess, everything proceeds as normal until a piece is captured. When this happens, the captured piece is immediately reborn on its home square in the initial game array. So, if the white queen is ever captured during the play, she will immediately reappear on d1. (The black queen would immediately reappear on d8.) Rooks, bishops and knights are reborn on the home square of the same color as it was captured on. For example, a white bishop captured on a white square would be reborn on f1. Pawns are reborn on the same file as they are captured on. If the rebirth square is occupied, then the captured piece just vanishes, as in normal chess.

It may sound confusing, but I promise that all will become clear from this example.

So let's have a look. If this game were being played under normal rules, then it would be a very simple problem indeed. White would play something like 1. Ng5+ Bd5 2. Bxd5 and that would be mate. But this is Circe chess, which means that the black bishop that was just captured on d5 (a white square) is immediately reborn on c8. The position is now this:

As you can plainly see, this is not mate. Black just moves his bishop to b7, and white is thwarted.

White must be more subtle. The key move is 1. Kb4!

This is a waiting move whose main purpose is to clear the a file. That's important! Now, any capture of the white rook on e1 will cause it to be reborn on a1, where it pins the black bishop.

Black needs to make his move, and towards that end we might notice the pawn on d2. It can promote by taking the white rook on e1. At this point you might sense a forthcoming Allumwandlung, which is a theme we have seen a couple of times in this series. It refers to a problem in which all four promotions appear at some point. Let's see how white deals with each of the promotions.

The queen promotion is probably the easiest to deal with. After 1. ... dxe1Q+ 2. Nxe1:

It is mate, since the black queen, newly reborn on d8, is helpless to block the check from the white bishop.

But how do we handle the rook promotion? After 1. ... dxe1R 2. Nxe1 the rook is reborn on h8, like this:

It is not mate, since the reborn black rook just takes the bishop. So, instead, white must play the interference move 2. Ng1:

And that is mate.

What about the bishop promotion? If you think white can just take the bishop with his knight, then look again! After 1. ... dxe1B+ 2. Nxe1, the black bishop is reborn on f8, where it checks the white king. I wanted to show you a picture of that, but Houdini won't allow me to produce a diagram where both kings are in check.

So, instead of taking white must play another interference with 2. Nd2 mate.

That only leaves the knight promotion. After 1. ... dxe1N, the black knight is poised to interpose on g2. Taking it doesn't help. since 2. Nxe1 causes the knight to be reborn on b8:

which is not mate, since the knight just jumps to c6. But now white has the simple 2. Qe4 mate.

Great stuff, but we've saved the best for last. Perhaps you are wondering what happens if black simply moves his bishop. Well, let's pick a square, say g8. Then we have 1. ... Bg8 2. Ra7 mate:

Are you thinking that black can just take the rook with his king? Well think again! If black captures the rook, it will be immediately reborn on a1, and black will still be in check. That's right! In Circe a piece can protect itself.

The annals of fairy chess, by which we mean chess played with unusual rules or with pieces not seen in the normal game, are vast. Many fairy conditions or fairy pieces never really catch on. But Circe has turned out to be remarkably fertile, and some lovely effects can be achieved in the genre. I'll show you a few more examples in the weeks to come.

See you next time!