One thing I left out of the making-of story about the squeezed state BEC paper last week happened a while after publication-- a few months to a year later. I don't quite recall when it was-- I vaguely think I was still at Yale, but I could be misremembering. It's kind of amusing, in an exceedingly geeky way, so I'll share it, though it's also a story of an embarrassing mis-step on my part.
So, the physical situation we were studying is described by the "Bose-Hubbard Hamiltonian": Bose because it's dealing with bosons (there's also a Fermi-Hubbard version, I believe); Hubbard after [mumble] Hubbard, who invented it; and "Hamiltonian" because the central equations used to describe non-relativistic quantum physics are Hamiltonians, a carry-over from classical physics. This is a well-studied system, mathematically, because it shows up when you're thinking about superfluid systems in liquid helium and the like. I read at least a dozen different theory papers looking at the states of a double-well system described by the Bose-Hubbard Hamiltonian.
The one thing that these papers all agreed on was that the Bose-Hubbard Hamiltonian is the sum of two terms: one of them describing the energy associated with particles moving back and forth between the two wells, and the other an energy associated with interactions between atoms. As I described in the write-up of the paper, the competition between these two terms drives everything.
What none of these papers agreed on was what to call the parameters expressing the strength of the two terms. There were at least as many notation systems as research groups investigating the question. And, on top of that, when we started writing the paper, we realized we didn't like any of them. So we made up our own-- "we" here meaning mostly me. I picked some symbols that were kind of a mix of various notations that I sorta-kinda liked, and mashed them together to make this:
(It's also the featured image at the top of the post, but I'll go easy on the handful of people still reading via RSS in this post-Google Reader wasteland...)
The "a" symbols refer to operations that move atoms around; don't worry about those. The first term in this is the tunneling term, and its strength is set by a single parameter we called γ, which stands for an integral over the wavefunctions of atoms in the two different wells. The second term is the on-site energy resulting from collisions between atoms in the same well, and that's set by a bundle of constants that we separated out to make a point: N is the number of atoms in the system; g is a coefficient describing the strength and nature of the collisional interactions, and β is an integral over the wavefunction occupied by the atoms in a particular well. The definitions of γ and β we stuck in a footnote:
We had reasons for doing things this way: a lot of other systems lumped the total number, or the collisional strength, or both together with the integral for β in a way that hid the influence of those things. We wanted them to be separated out, so as to make clear that the interaction depended on the number and the character of the collisions. I picked these symbols, and we started using them for everything. It was yet another notation system introduced for this same problem, but there's nothing in principle wrong with that.
The problem is subtle, and I actually missed it when I was setting this up, until I started doing simulations of the behavior of the system: because these two effects are competing with each other, the two terms really ought to have opposite signs. Really, they do, because if you look closely at the definitions, and re-write them in another way, you can show that the value of the parameter I called γ is a negative number. When I was writing code, I got nonsensical results until I stuck a negative sign in front of my values for γ, at which point everything worked nicely.
There's nothing in principle wrong with this-- after all, we gave the definition, and people could work out for themselves that γ defined in this manner is less than zero. It is, however, somewhat contrary to the general practice of physics. The usual default is to assign symbols to positive numbers, and pull the sign outside so it's explicitly visible. This comes up all the time in intro classes, where by convention we define the acceleration of gravity near the Earth's surface as g=+9.8m/s/s, and put the negative sign for the downward direction in by hand-- students are forever trying to make g=-9.8m/s/s, and also use the negative sign outside the symbols, leading to nonsensical results involving things rocketing off into space at 9.8 meters per second squared.
Well, with my cobbled-together notation, I had managed to define γ to be a negative number, which isn't normally done, at least not without telling people. And, sure enough, it tripped somebody up: some months after our paper was published, I got sent a referee request for a theory paper about BEC in the Bose-Hubbard Hamiltonian, talking about all these cool states you could create. This was from, I believe, a group in China, and I was actually the third referee brought in to settle an argument-- one of the first two referees had pointed out that their results made no sense in a couple of simple limits, and that the whole paper should be thrown out. In their response, the authors started a sentence with "As you can clearly see from Equation 1 of Orzel et al.,..."
It turns out, they were using positive values for γ and getting the same nonsensical results I had when I started doing simulations. Of course, I knew what the experiment really looked like, so I found the error quickly; they just assumed that I had known what I was doing.
Now, it turns out that the results they were getting do, in fact, correspond to a real physical situation-- where the interactions between atoms are effectively attractive, rather than repulsive. This is the meaning of the g parameter in our equation above, and if you make that negative, it lowers the energy of the system as you add more atoms to a single well. So their calculations were, in fact, reasonable answers, just not for the system they thought they were describing...
(By the way, this attractive-interaction system also produces interesting quantum phenomena, in that the ground state of the system is a Schrödinger cat state, with all the atoms in one of the two wells, but equal probability of it being either of the two. To the best of my knowledge, though, I don't believe anybody has done the experiment, which would be tricky for a number of reasons. But kind of cool.)
Anyway, as the tie-breaking referee, I had to settle this by pointing out (in the third person, of course) that Orzel et al. were, in fact, dumbasses, who had defined their parameters in such a way as to make γ negative. I did try to lessen the impact by pointing out the cat-state thing, but I don't think it worked. At least, for the little while after that when I was actively following the situation, I never saw a resubmission from those authors re-casting it as a cat-state system. I never heard anything more from the journal, either, so I assume the authors just conceded the point and withdrew the paper.
I feel a little bad about that, actually, because it means I'm personally (partly) responsible for what was undoubtedly the very worst week of some poor grad student's life. But only a little bad, because they did, in fact, have all the information they needed to figure out the right answer, and all I did was make it slightly more difficult...

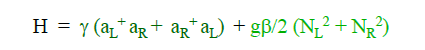
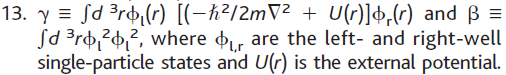
If you have never been involved in the rejection of a paper, either as author or as referee, you have lived a sheltered scientific life indeed. I've rejected some, and had some rejected. I don't think any of the papers where I recommended rejection were due to misapplying results from my own papers (apart from the one that copied several paragraphs verbatim from one of my papers--that turned out to be a paper with some original parts, and some true parts, but none of it both). But I did encounter a manuscript where the authors failed to ensure that the argument of a special function was dimensionless (as the argument of anything more complicated than a polynomial must be).
I’ll go easy on the handful of people still reading via RSS in this post-Google Reader wasteland
Thanks!
(I'm using InoReader. It's not quite mature yet, and it's not exactly like Google Reader was, but it's close enough for me. I recommend it. I may even donate something to them for keeping me from RSS withdrawal!)
RSS (and Atom) existed before Google Reader, and will continue to exist after it. It remains the easiest way to follow multiple blogs, especially when some of them have low and/or uneven publication rates. There are several RSS/Atom readers. I currently use the NewsFox plugin for Firefox, and Early Edition 2 for iPad.
As for the sign issue -- getting back on topic -- I certainly feel for the poor group who misread the paper, and it is a general pain in the back side when each paper has its own idea of notation. However, the form given for gamma conforms with the usual way of writing the single-particle term of a Hamiltonian, so in a way it is a more sensible notation than extracting the minus sign.