Last time in our trip through the cold-atom toolbox, we talked about light shifts, where the interaction with a laser changes the internal energy states of an atom in a way that can produce forces on those atoms. This allows the creation of "dipole traps" where cold atoms are held in the focus of a laser beam, but that's only the simplest thing you can use light shifts for. One of the essential tools of modern atomic physics is the "optical lattice," which uses patterns of light to make patterns of atoms.
OK, what do you mean "patterns of light"? Well, remember, light has both wave and particle properties, and physicists looking at the interaction of light and atoms will cheerfully switch back and forth between those pictures, sometimes in mid-sentence. Optical lattices rely on the wave nature of light to create structured arrays of "traps" for atoms.
The simplest version of an optical lattice is made by two beams of light with the same polarization headed in opposite directions; usually, people do this by bouncing a single beam off a mirror that sends it back exactly along original path. The two beams each behave like waves, and when you add those waves together you get a pattern known as a "standing wave."
How does that work? Well, when you bounce the light off the mirror, you just reverse the direction of the wave, which keeps oscillating with the same frequency and wavelength. It turns out that the effect of this is to exactly cancel out the original wave right at the surface of the mirror-- if the incoming wave has a positive peak, the outgoing has a negative peak, and those add to give nothing. Since the two have the same wavelength, there's another spot half a wavelength away where they cancel again, and half a wavelength after that, and so on. These are called "nodes" in the wave, and are spots where there's no light at all, because the two waves interfere with each other.
So, two lasers going through the same space give you nothing at all? In places. In between those places, though, you get lots and lots of light-- the two waves add together to give you a bright spot every half-wavelength (these are "anti-nodes" of the standing wave). The total energy in the light field stays the same, but it's shifted from a uniform beam to a collection of bright and dark spots, with neighboring bright spots separated by half a wavelength.
And these act like dipole traps? Exactly. The presence of the light field shifts the energy levels of the atoms, and if you choose your laser frequency to be lower than the natural frequency the atoms want to absorb, the energy of an atom in one of the bright spots will be lower than the energy of the same atom in the dark spots. If you put in sufficiently cold atoms, this will give you a set of regularly spaced "wells" where the atoms are trapped by the light.
And this is interesting... why? Well, because it's a simple realization of the most basic analogue of solid matter: a one-dimensional periodic potential. If you think about a microscopic picture of a solid, you have a long row of atoms that are bound together in a crystal. The nuclei of these atoms are positively charged and very heavy, so they basically don't move, but the electrons are light and range farther afield. If you want to determine the behavior of electrons in a solid, you need to include all of the atoms in the crystal, and the simplest version looks exactly like what you get from a standing wave: a regularly spaced line of wells where electrons have lower energy.
Yeah, but how much can you do with only one-dimensional systems? It's an incredibly rich system, actually, and hasn't remotely been exhausted after the better part of a century of people playing around with it. Having the ability to do experimental investigations of these systems with atoms playing the role of electrons has only increased the interest in this sort of thing.
But you're not limited to just one-dimensional standing waves. If you take a second pair of beams (or a second beam reflected back on itself), at right angles to the first set, you can make a two-dimensional pattern of bright and dark spots. That gives you a system where the energy of the atoms looks kind of like an egg crate, as seen in the three-dimensional plot that's the "featured image" for this post, which I'll reproduce here:
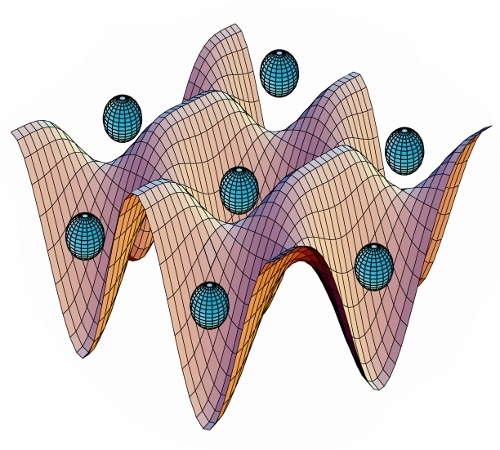The famous optical lattice potential picture, from the Rolston group web site (http://www.physics.umd.edu/rgroups/amo/rolstonwebsite/bec.htm )
The "egg crate" surface here represents the energy of an atom in the lattice, and the balls floating above it represent trapped atoms. Yes, this is kind of a mixed visual metaphor, but it gets the idea across.
(Amusing story about this picture: This originates with somebody in the lab at NIST where I did my grad work-- maybe Poul Jessen, who finished up right around the time I joined the group. It was, as you might guess from the color scheme, generated in an old version of Mathematica, and was a huge pain in the ass to make. The image existed as a gigantic high-resolution bitmap file (by 1993 standards, anyway), and took forever to open, let alone edit. But it turned up in just about every optical lattice talk in the six years I was at NIST, because nobody wanted to deal with the hassle of making a new version...)
If you add a third pair of beams, perpendicular to the fist two, you can make a simple cubic lattice of bright and dark spots, and get a three-dimensional array. This looks like the crystal lattice of a simple solid, thus the name "optical lattice." (There was one German group back in the day that used to use "optical crystal" instead, making it a dead giveaway when they refereed one of our papers, but "lattice" is the most common term by far.)
So, you can study the behavior of simple cubic solids? That's the easiest thing to do, yes, but you can make all sorts of patterns with different arrangements of beams. And these days, a lot of people use holographic masks to generate arbitrary intensity patterns floating in space, so in principle, you can put your ultra-cold atoms into any structure you care to study.
Lattice systems are one of the most exciting areas in cold-atom physics, and I've written up a lot of optical lattice physics over the last several years of blogging. This is, incidentally, the phenomenon that prompted this series of posts-- when I was writing up my squeezed state paper, I had to mention the one-dimensional optical lattice we used to break the BEC up into pieces, and couldn't spend much time on it. I thought "Gee, I really ought to have something to point to about the physics of lattices," which eventually led me to this series of posts...
Yeah, this is pretty cool. Who would've thought bright and dark spots would be so interesting? Actually, it's not just bright and dark spots. There's actually another, more subtle effect that can come in, that ties in to the lower-than-expected temperatures I've been teasing for the last few posts. You can also make a lattice based on patterns in the polarization of the light.
OK, what? Well, when I mentioned the simple idea above, I specified that the two light waves needed to have the same polarization to get a standing wave. If you do something to flip the polarization of one of the beams, then the light waves are oscillating in different directions, and you get a uniform light intensity everywhere in the sample.
That does not, however, mean that there is no interference pattern. You get a uniform intensity, but not a uniform polarization--in fact, you get a "polarization gradient" where the light has different polarizations at different points in the lattice-- vertical in one place, then right-hand-circular, then horizontal, then left-hand circular, then vertical again.
And this is important... why? Because it turns out that different polarizations of light interact differently with different atomic states. And in the words of a famous misquotation of Bill Phillips, there are no two-level atoms, and sodium is not one of them. The real atoms people use in laser-cooling experiments have multiple energy states, whose interaction with light depends on the polarization of the light.
This means that, when you have a light field where the intensity is uniform but the polarization changes from place to place, you still get an array of wells where the atoms would like to be trapped, but the individual wells trap different states. You end up with something like two interpenetrating simple cubid lattices.
So, like a salt crystal, where you have a sodium, then a chlorine, then a sodium, then a chlorine, and so on? Yes, kind of like that. The atoms are the same element, but different internal states. This kind of patterning gives you another set of tools to play with-- you can push the internal states around by applying magnetic fields and radio-frequency light fields, which lets you make a lattice of double-well potentials (one atom in each of two states, trapped side-by-side and well separated from other atoms), or shift the two lattices relative to one another, or even make crazy patterns like a lattice of little ring-shaped traps.
And this also has something to do with lower-than-expected temperatures? But I thought you said in the dipole trap post that these light-shift forces couldn't do any cooling? By themselves, they can't, because the light-shift potentials you make this way are conservative. There's one more piece of the puzzle, though, that adds a dissipative component to the process, and lets you do extremely effective cooling. But this is running long enough as it is, so--
Let me guess, you're going to split it off into its own post. Yep. See you next time for an explanation of "Sisyphus cooling."
- Log in to post comments