One of the labs we do in the introductory E&M class I'm teaching this term involves investigating charged particles with sticky tape. If you haven't seen it before, "invisible" tape picks up an electric charge when it's peeled off a surface quickly, and with a little care, you can create both positively and negatively charged tapes and investigate their interactions.
For Monday's class, I wanted to do a demonstration of one of the questions we were discussing, which involved the attraction between two objects with opposite charges and how that changes when you insert something between them. So I set up a pair of oppositely charged tapes and brought them near each other. It turns out to be really hard to see the effect, though, because the interaction is really touchy. If the tapes are too far apart, there's no appreciable deflection, but if you bring them too close together, the attraction pulls them right together. There's only a narrow range in which the tapes are attracted enough to clearly see the attraction, but not pulled together so strongly that they stick to each other. I made a little video to illustrate this:
There is very clearly a tipping point to this experiment-- a starting distance between the two tapes where they suddenly swing together-- and that got me wondering how to understand this behavior. On a conceptual level, of course, this happens because the force between the charged tapes increases rapidly as they get closer together, more rapidly than the force that keeps the tapes apart (which ultimately comes from gravity). But I wanted to see if I could get a more quantitative understanding of where the tipping point is.
Unfortunately, when I started writing down equations, I rapidly discovered that this is kind of a mess. There are two different trig functions involved in looking at the behavior of the tapes-- the distance between them depends on the sine of the angle the tape makes with the vertical, while the restoring force depends on the tangent-- and the resulting equation is kind of awful. So I did what any good physicist would do: I switched to looking at a toy model that's simpler to work with.
The basic situation is that we have two charged particles attracting each other, with another force that attempts to hold them apart. To simplify the math, I switched to a simpler situation that captures the same physics. Instead of two tapes free to move, I considered only one moving particle, imagining the other held fixed. Rather than a tape hanging at an angle with all the trig functions that implies, I looked at every physicist's favorite force model, a mass on a spring obeying Hooke's Law. The revised scenario looks like this:
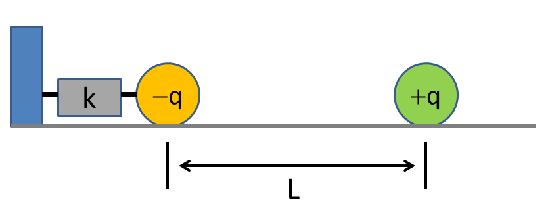 The toy model of the charged-particle detection discussed in the text. Two charges start out a distance L apart, one of them is attached to a spring with spring constant k.
The toy model of the charged-particle detection discussed in the text. Two charges start out a distance L apart, one of them is attached to a spring with spring constant k.
Taking the equilibrium position of the spring without the positive charge in place as x=0, and the initial separation as L, we expect the charge on the spring to be stretched out to some point x by the attraction between particles. As it stretches, the spring force increases, but so does the electrostatic attraction. If the force between charges isn't too big, there will be a point where those two forces balance, and the charge will sit in equilibrium; if the charges get too close together, though, the electrostatic force will increase to a value the spring can't match, and the two will get pulled together.
In order for a stale equilibrium to exist, you need the force from the spring:
$latex F_{spring} = kx $
(where k is the spring constant) to have the same magnitude as the force between the two charges:
$latex F_{elec} = \frac{1}{4 \pi \epsilon_0} \frac{q^2}{(L-x)^2} $
The game here is to find the value of x for which this works out. If that's between 0 and L, then there's a solution; if it's great than L, then the two charges will come into contact.
How do we do this? Well, we set the two forces equal, and find a common denominator by multiplying the spring force by $latex \frac{(L-x)^2}{(L-x)^2} $. Once we do that, we can work with just the numerator, and get:
$latex (L-x)^2 kx = \frac{1}{4 \pi \epsilon_0} q^2 $
If we expand out the squared term on the left, this is:
$latex (L^2 - 2xL + x^2)kx = \frac{1}{4 \pi \epsilon_0} q^2 $
This looks like a mess-- I have to have an idea of what the charge is, and the separation, and the spring constant. I don't want to actually estimate all of those things, because it's easy to come up with numbers that are completely wacky. But I can resort to another very physicist-y trick, namely the use of dimensionless variables.
The first step here is to factor out an $latex L^2 $ from the stuff in parentheses on the left. This gives me:
$latex L^2(1 - 2(x/L) + (x/L)^2) kx = \frac{1}{4 \pi \epsilon_0} q^2 $
That gets halfway there, but I've still got that kx floating around. I can multiply and divide that by L, though, getting:
$latex L^2(1 - 2(x/L) + (x/L)^2) kL (x/L) = \frac{1}{4 \pi \epsilon_0} q^2 $
Now everywhere I have a position, I have it in the form (x/L), which removes the need to worry about the units. I'm expressing the position as a fraction of the initial separation, a number between 0 and 1 (if I have a stable equilibrium, anyway...).
Of course, I still have a couple of L terms on the left-hand side, and that pesky k, so let's clean that up a little by dividing both sides by all those things. when I do that, I get:
$latex (1 - 2(x/L) + (x/L)^2) (x/L) = \frac{1}{4 \pi \epsilon_0} \frac{q^2}{L^2} \frac{1}{kL} $
That may still look like a mess, but I've grouped those terms on the right-hand side the way I did for a reason. this breaks down into two pieces, both with units of force. One is the electrostatic force at the starting position:
$latex F_{elec,min} = \frac{1}{4 \pi \epsilon_0} \frac{q^2}{L^2} $
I've labeled it with the subscript "min" because this is as small as the electrostatic force will get-- as the charges pull together, this force will only increase. The second units-of-force term shows up in the denominator, and is the spring force:
$latex F_{spring,max} = kL $
I've labeled this with the subscript "max" because this is as big as the spring force can get-- it's what you would see if the spring were stretched out all the way to bring the two charges into contact.
So, switching to dimensionless units both removes the need to estimate quantities, and gives us some physical insight. Assigning a new symbol to the dimensionless length, we end up with a very simple equation:
$latex \rho^3 - 2\rho^2 + \rho = \frac{F_{elec,min}}{F_{spring,max}} $
The stuff on the left is an equation for the equilibrium position as a fraction of the initial separation, and the stuff on the right is a ratio of the forces. All we need to do is solve this equation and see what the value of $latex \rho $ is.
Of course, that's a cubic equation, which means I'm not about to work it out with pencil and paper. Happily, here in the century of the anchovy 2014, we have Wolfram Alpha, and I can just crank this in and look for solutions for particular choices of the force ratio.
What you find when you do this is that for values of that ratio greater than 4/27, there is no value of $latex \rho $ between 0 and 1 (the solutions are all around 1.3, but that's not a real answer, because the equations I set up above don't work for $latex \rho > 1 $ -- all that matters for our purposes is that there isn't a valid equilibrium point above that level).
So, if the combination of charges, initial separation, and spring constant is such that the electrostatic force at maximum separation is greater than 4/27ths of the spring force at maximum stretch, it's impossible to avoid having the two charges come into contact. If it's smaller than 4/27ths, you cna find a point where the spring stretches by something less than a third of the separation, and the system will sit there happily. Which is exactly the "tipping point" behavior we see with the tapes-- get them too close, and there's no way to keep them from touching.
There are still some kind of mysterious aspects to this-- why 4/27 specifically?-- but this is a nice illustration of a couple of physicist tricks and why they're useful. Switching to a toy model of the system got me something that's much easier to understand mathematically, but reproduces exactly the same behavior as the more complicated real system. And changing to dimensionless variables both avoided the need to come up with specific numbers for charges and separations and produced a situation where the big jumble of symbols could be interpreted in terms of simple physics: the maximum and minimum forces involved. this is a very general phenomenon, and something it takes a little while to appreciate-- physicists are forever switching variables, not because we're lazy and don't want to keep writing all the symbols, but because changing to a dimensionless set of variables often provides some insight into the underlying physics.
This ended up being way more complicated than I could use in the class I'm teaching this term without making a few heads explode, but it makes me very happy, in an extremely nerdy manner. So I'm sharing it with you. I suspect the original tape problem will remain intractable-- there are those pesky trig functions, plus a couple of additional parameters-- but this 4/27 thing might be something you could test with the "Coulomb balance" apparatus we have, which is a little closer to the situation described here. That might allow a little more quantitative control of the charging than you can get with sticky tape. I may check that out at some point. Or, more likely, try to find a summer student who could test it out for me...
- Log in to post comments




That's pretty easy:
consider the function
in the interval [0,1]. There is one special extremal Point (local maximum) at 1/3 with F(1/3) = 4/27.
Btw, F(0) = F(1) = 0.
I know that 4/27 gives that as a solution, but it's kind of an odd number. The 27 sorta-kinda makes sense as the cube of three, but 4 isn't the cube of anything. So it's not obvious to me where that particular fraction would come from.
This is in contrast to simpler calculations where you can see the origin of the numbers that turn up. If there were two springs, say, instead of a spring and a charge, you would expect the equilibrium position to depend on the ratio of the spring constants, and that would make some physical sense in addition to just being the solution spit out by turning the crank on solving the equations.
I guess this is another physicist-y attitude: we don't really trust math per se, but want solutions to make some intuitive sense...
The 4/27 is actually interesting here as these are two constants that feature prominantly in the algebraic (non-wolfram-derived) solution to the cubic: Cardano's method.
Anyway, instead of looking for the point(s) of equilibrium specifically, I think it's more useful to look at the entire force formula for all 0 < x L, and dips in the middle due to kx. (Plot it!!) If k is large enough, the function can dip below the x-axis to become negative for a brief portion between between these two points.
While the function is positive, the particle is being pulled to the right. While the function is negative, the particle is pulled back left. The goal then is to make k large enough to generate the negative interval. The function then should be stable if x is close enough to the roots of F(x), and the particle isn't moving too much.
The part I don't know is whether, despite being close to these roots, the particle can potentially gain enough energy to eventually tunnel out of these points. The left hand root would seem to be stable, but for the right hand root close to the second chage, could a particle started at rest near this root eventually escape equilibrium?
P.S.
Could the ratio also be expressed as a ratio of maximium potential energies of the two forces? 2*(C/L)/(kL^2). Does that work?
The force function did not appear in my post above for some reason: I'll write out the post again
Anyway, instead of looking for the point(s) of equilibrium specifically, I think it’s more useful to look at the entire force formula for x between 0 and L. Let C=q^2/(4 pi epsilon) so that
F(x)=F_charge-F_spring = C/(L-x)^2-kx
This function starts out slightly positive, blows up positively as x goes to L, dips in the middle due to kx. (Plot it!!) If k is large enough, the function can dip below the x-axis to become negative for a brief portion between between these two points.
While the function is positive, the particle is being pulled to the right. While the function is negative, the particle is pulled back left. The goal then is to make k large enough to generate the negative interval. The function then should be stable if x is close enough to the roots of F(x), and the particle isn’t moving too much.
The part I don’t know is whether, despite being close to these roots, the particle can potentially gain enough energy to eventually tunnel out of these points. The left hand root would seem to be stable, but for the right hand root close to the second chage, could a particle started at rest near this root eventually escape equilibrium?
P.S.
Could the ratio also be expressed as a ratio of maximium potential energies of the two forces? 2*(C/L)/(kL^2). Does that work?
Actually, as I look at the function again with my brain turned on, it is of course stable at the left hand root but unstable at the right hand root.
I suppose I may as well let Wolfram alpha show what I mean. The wonders of modern technology.
Here's a manual forward trackback to the next post talking about sticky tape: ping