Before going to the playground Saturday to investigate non-intertial frames, SteelyKid and I went over to campus to do some experiments in relativity. Galileian relativity, that is:
What you see here is SteelyKid sitting on a rolling lab cart with a camera bolted to it. She throws a ball up in the air a couple of times with the cart at rest, then I start pushing it across the room, and she tosses the ball a few more times. You can see from the video that, other than the motion of the background, the two cases look very similar.
This is a demonstration of the principle of relativity, which goes back a whole lot farther than Einstein in 1905. This version is usually credited to Galileo in the early 1600's (though I'm sure Thony C. will leave a comment pointing out that many others did it before Galileo), and just says that the laws of mechanics are the same whether you're at rest, or moving at constant speed. Galileo was invoking it in support of heliocentrism, to rebut the argument that if the Earth was really a spinning ball, we would notice it. He points out, using the example of a moving ship, that there's really nothing you can do that lets you distinguish between the case where you're at rest, and the case where you're moving at constant speed-- all the physics you can see will look exactly the same.
Einstein's big achievement was to extend this to all of physics, including the new physics of electromagnetism that had been invented in the nearly 300 years since Galileo. That brings in the requirement that the speed of light be constant for all observers, with all sorts of fun consequences for space and time.
So, the video above is a cuter version of Galileo's thought experiment, but how good is it really? I mean, it looks pretty much the same, but it's hard to be quantitative about this.
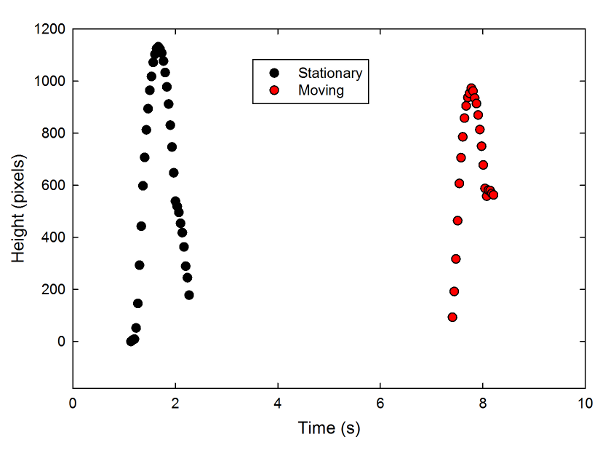
Happily, in the 400-odd years separating us from Galileo, we've invented computers, and Tracker video analysis. So I cranked the above clip into Tracker, and measured the position of the ball as a function of time for two of the higher tosses, one while the cart was sitting still, one while it was moving:
The position of the ball as a function of time for two tosses.
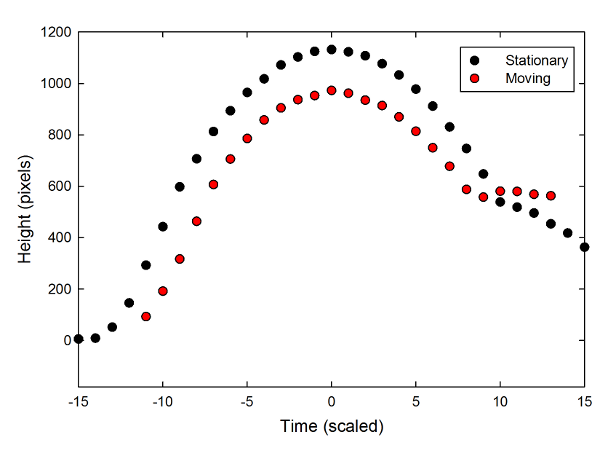
If I wanted to be super-precise about this, I would calibrate the distance scales, and all that, but I don't really care that much. For the purposes of this blog post, it's enough to show that the two trajectories are governed by the same laws of physics. So I can just work with the height in pixels and the time in frame number, and move the data around so that the maximum height of each toss occurs at the same time:
The height of a thrown ball as a function of time, for both stationary and moving cart.
You can see that in both cases, there's a little acceleration at the start, then a nice round parabolic curve in the middle, which is interrupted on the way down. On the stationary cart, SteelyKid catches the ball, and the downward acceleration of gravity gives way to a downward acceleration as she moves the ball. On the moving cart, the break is a little more abrupt, because the falling ball actually bonks her on the nose.
The moving toss doesn't go quite as high-- SteelyKid isn't all that consistent a ball launcher-- but you can see that the curvatures of the parabolas are very similar. If I fit a parabola to the central section of each, I get acceleration values of 6.28±0.04 pixels/frame/frame for the stationary table, and 6.8 ± 0.2 for the moving table. While those uncertainties make this look like a statistically significant difference, I wouldn't put much stock in that. There's a fair bit of motion blur in the images, because the frame rate's not all that high, and there's a lot of jitter in the moving case (I braced the camera as best I could, but it wobbles). I'd say this shows there isn't a really dramatic difference in the way physics works in these cases.
Ah, but what about along the direction of motion? After all, if things were going to get weird, that's probably where we'd expect to see it. Well, here's a graph of that:
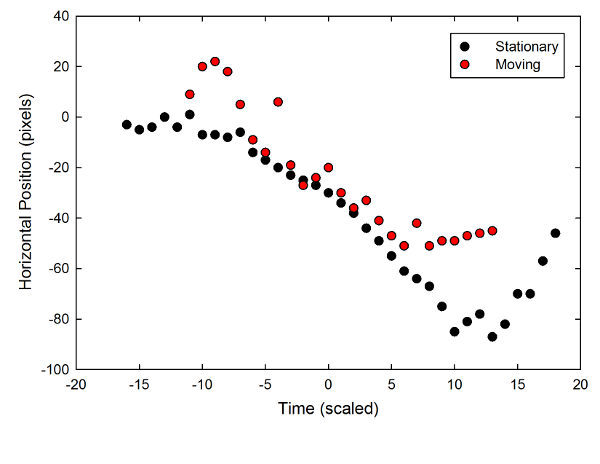The horizontal position of the thrown ball as a function of time, for both stationary and moving cart.
If you can see a clear difference between the two of those, particularly in the time from -5 to +5 when the ball is clearly in free flight, you're doing better than I am.
So, Galileo was right, Einstein was right, and physics does not depend on how you're moving. Also, SteelyKid is the cutest lab assistant in modern science. Best of all, she works cheap-- I bought her participation with a couple of bucks of frozen yogurt at TCBY...
- Log in to post comments
More like this
…though I’m sure Thony C. will leave a comment pointing out that many others did it before Galileo.
Just for that I won't comment.
"Einstein’s big achievement was to extend this to all of physics".
This is a common comment, but I don't think it is fair to Galileo (and predecessors). There is a good reason to believe that Galileo considered relativity an universal principle. If a principle is universal, you can't extend it anymore, right?
I mean that in the sense of "extended it to physics that was not known in Galileo's day." I'm sure Galileo regarded it as universal, but Galileo didn't know about Maxwell's Equations.
My point is, let us assume that you proposed some principle and declared it to be universal. And this principle is renamed after another guy whenever new physics is discovered and confirmed to obey it. Would this be fair?
That is an excellent question, Alexey.
I've never read any of Galileo's original writings, so I don't know if he only asserted it in its most general form (the form that Einstein used) or if he specialized it in the form that is inconsistent with Maxwell's equations' description of electromagnetic radiation.
CCP @5: In Galileo's day the speed of light wasn't known to be finite--that discovery came several decades later. Furthermore, exactly zero of Maxwell's equations were known at the time--calculus hadn't been invented yet, either. So I'm not sure the question is even meaningful. Let the speed of light go to infinity, and special relativity becomes equivalent to Galilean relativity.
Agree, Eric, but I'm still curious whether he stated it as a principle or in a form equivalent to the equation that is now associated with "Galilean relativity". The latter was inconsistent with the new theory of Maxwell, while the former was not.
I'm curious because I have run across other instances where the actual physical ideas at the time are not what ends up in textbooks. Was it Newton or Coates or others seeking to apply Newton's mechanics who put Galileo's idea into that particular equation? Would it be better for the education of physicists if we presented the idea rather than the equation?
I'm not aware of Galileo using a mathematical formulation for it. The attribution to Galileo stems from a passage in the Dialogue where he recommends closing yourself up in the cabin of a ship with a wide variety of things, and observing that they all behave the same when the ship is moving as when it's at anchor. There's also apparently an earlier letter where he claims to have dropped something from atop the mast of a moving ship and observed that it still falls straight down. But both of those bits are descriptive passages, not equations.