The third of the great physics principles introduced in our introductory mechanics courses is the conservation of angular momentum, or the Angular Momentum Principle in the language of the Matter and Interactions curriculum we use. This tends to be one of the hardest topics to introduce, in no small part because it's the last thing introduced and we're usually really short on time, but also because it's really weird. Angular momentum is very different than linear momentum, and involves all sorts of vector products and things going off at right angles.
This leads to some of the coolest demos in the whole course, such as this classic involving a spinning wheel suspended at one end of the axle:
The spinning wheel remains nearly horizontal and precesses in a circle because of the Angular Momentum Principle. The spin gives the wheel a substantial angular momentum, which is directed along the axle of the wheel. Angular momentum can only be changed by a torque, which requires a force exerted at some distance from a pivot point. Gravity provides such a force, pulling on the center of the wheel at some distance from the suspension point, but the weird math of angular momentum means that the torque is at right angles to both the force of gravity and the axle of the wheel, so the gravitational torque makes the angular momentum rotate in the horizontal plane, which means the axle must rotate.
This is a cool trick, but it's also presented in a way that makes it seem a little magical-- angular momentum just is along the axis, and torque just is at right angles to the force, and deal with it. Which is one of the things making it so difficult to learn and to teach.
But, of course, this is a classical system, so all of its dynamics need to be contained within Newton's Laws. Which means it ought to be possible to look at how angular momentum comes out of the ordinary linear momentum and forces of the components making up the wheel. Of course, it's kind of hard to see how this works, but that's what we have computers for.
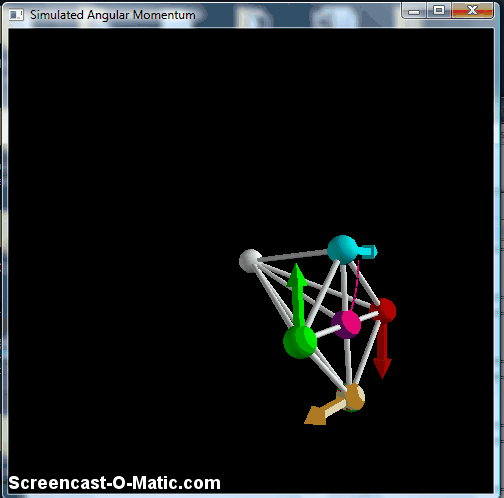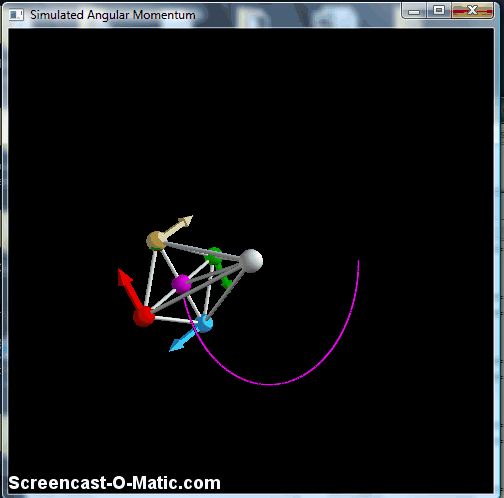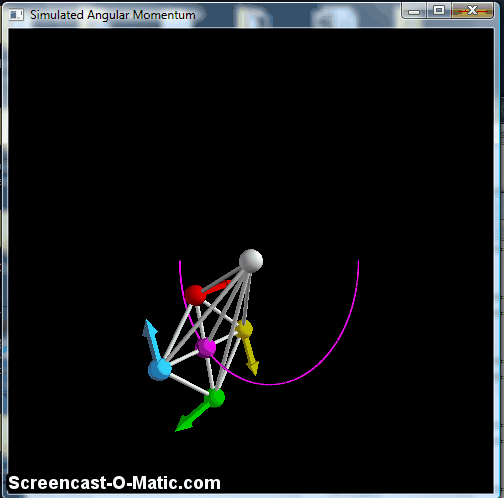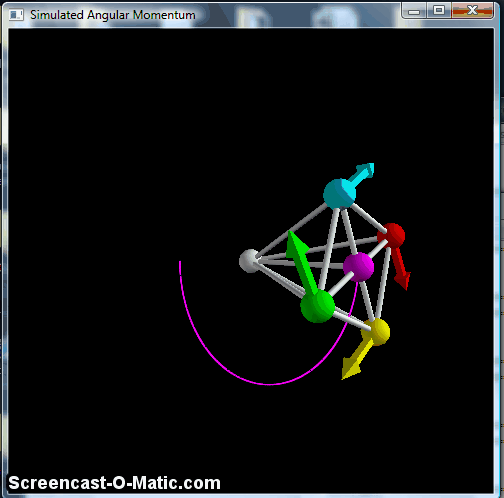
So, I wrote a VPython program to look at this, which I also put on the web with GlowScript, so you can play with it. Or point at my source code and laugh. The "featured image" up top is some of the output from the VPython on my desktop.
So, what have we got here? Well, there are six balls: a pivot point at the origin, and five balls some distance out, four of them connected to a central "hub." This is my simulated "wheel." I used four because I could put them on the x and y axes, and then not have to do complicated math to determine the velocity needed to make them go in a circle.
To make these spin, of course, I need some sort of force to bend them onto a curved path, otherwise they would just fly off in a straight line. That's accomplished by the four spokes connecting them to the central hub. These are simulated as "springs" with a very high spring constant-- you can see a bit of wobble in and out as the wheel spins, in this .gif of the output in a world with no gravity:
So, is this enough to produce angular momentum and the levitating wheel precession effect? Well, we can add a gravitational force and see what happens:
This actually has a little bit of the angular momentum thing going on, in that the "wheel" remains vertically oriented throughout. It doesn't keep the axis in the horizontal plane, though, but instead swings down and back like a pendulum. It also gets a little wobbly, and eventually the balls start to catch up to each other, which is probably some numerical weirdness.
We can fix that problem by adding cross-braces-- making the lines connecting the balls on the "wheel" into rigid springs. That gets us this:
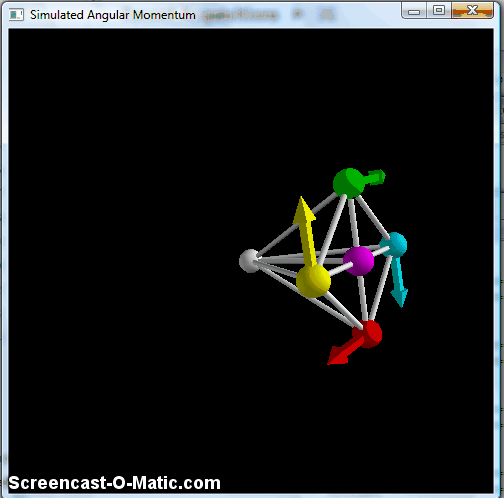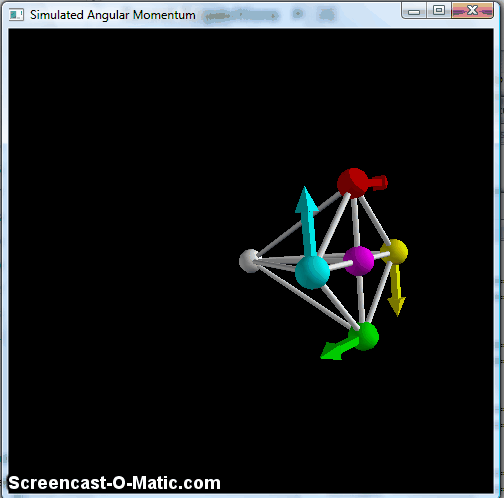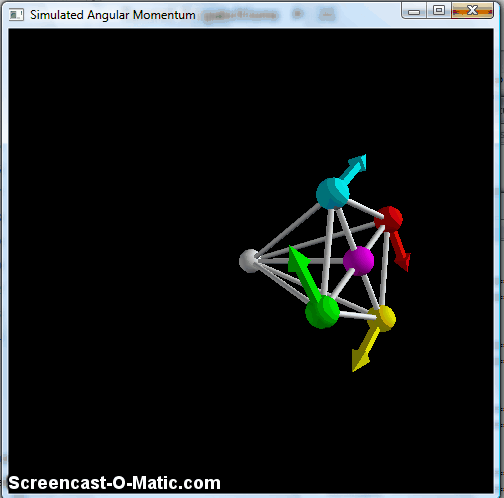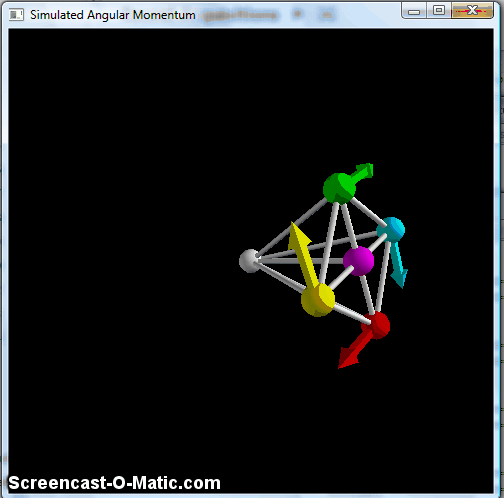
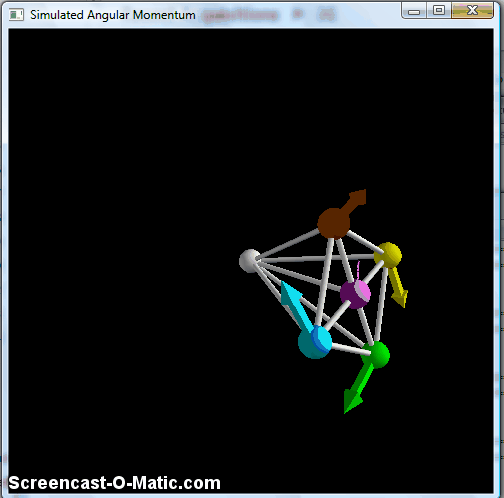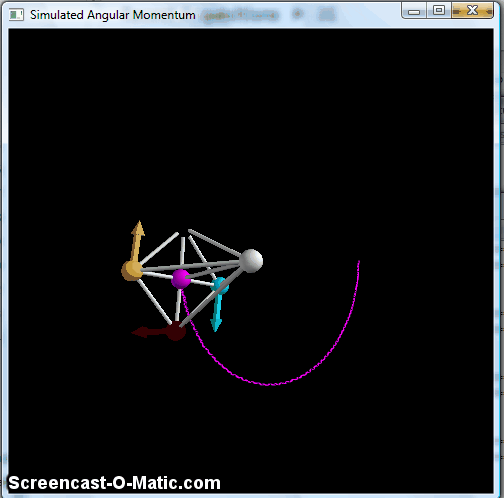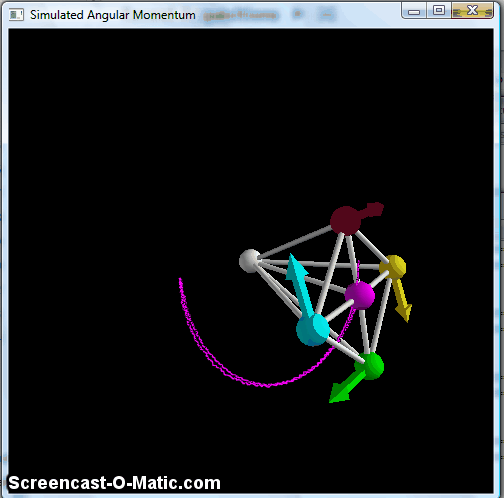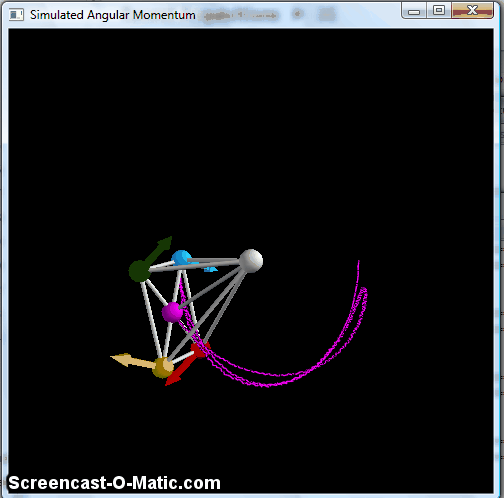
This does the same pendulum-type motion, with the "wheel" remaining vertically oriented, but avoids the part where the balls catch up to each other, so it's generally cleaner. But again, this doesn't keep the axle in the horizontal plane. To do that, we need one last piece, namely a way to keep the wheel perpendicular to the axle. This is accomplished by making the braces connecting the balls to the pivot point at the center into very stiff springs, at which point you finally get something that resembles the classic bicycle wheel:
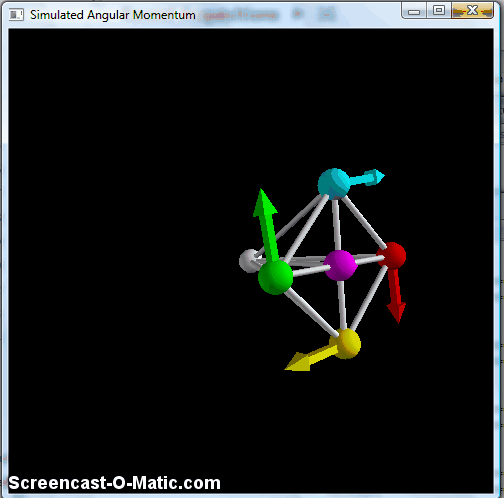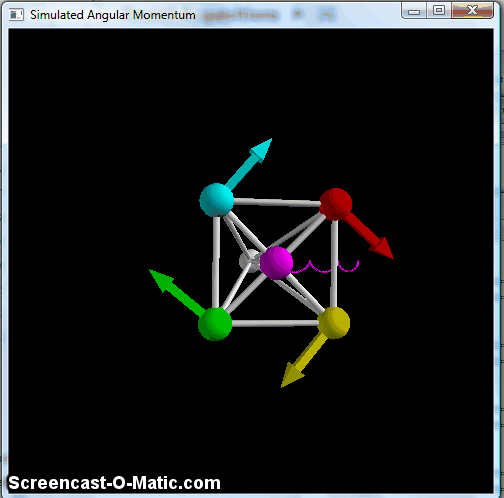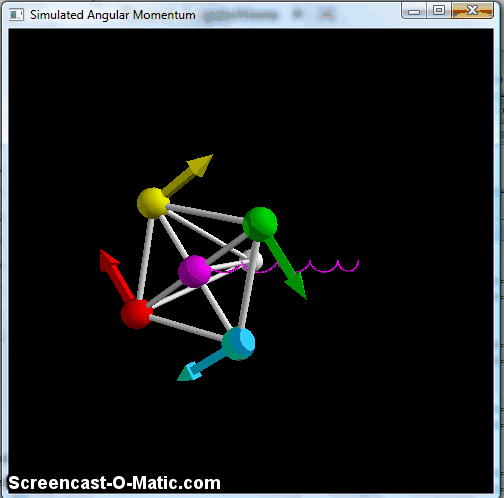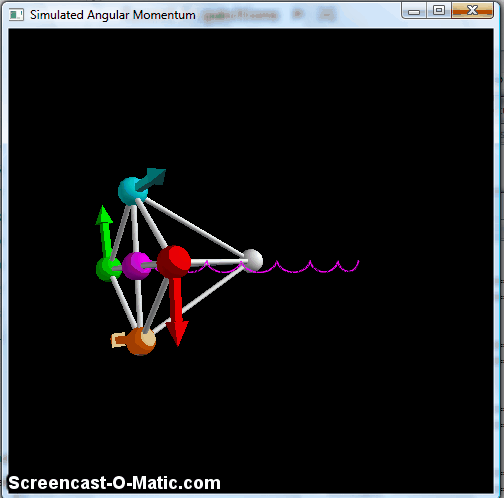 Simulated spinning "wheel" with all braces made into stiff springs, making it effectively a rigid object.
Simulated spinning "wheel" with all braces made into stiff springs, making it effectively a rigid object.
Here, you see the precession effect of the bicycle wheel, with a small up-and-down wobble. The technical term for this is "nutation," and it's a part of the phenomenology of angular momentum. There's a nice discussion in this arxiv paper, which also fulfills my contractual obligation to indirectly cite Feynman at least once a year. The nutation gets smaller as you make the initial angular momentum bigger, and tends to damp out pretty quickly-- you can see a little of it in that bicycle-wheel video above, but lots of lecture-hall versions of this start out with so little nutation that you really don't notice it at all.
(You can make the effect bigger and more complicated by playing with the parameters of the problem. If I reduce the spring constant of the braces holding the wheel perpendicular to the axle, for example, I can make it draw little loops:
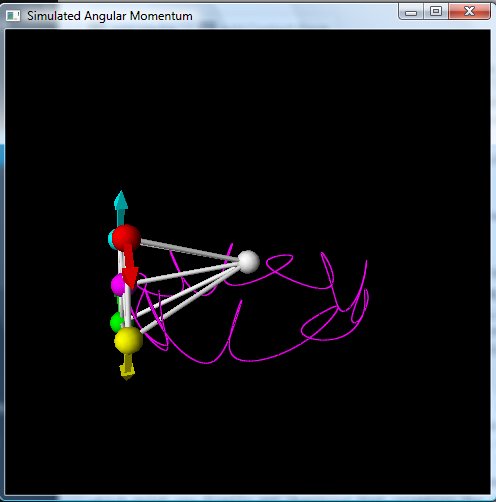 Screen shot of a simulation with the braces to the pivot point reduced to 1% of the initial spring constant.
Screen shot of a simulation with the braces to the pivot point reduced to 1% of the initial spring constant.
This is more like what you see in a spinning top, which is the other system where you can find people talking at length about nutation.)
The cool thing about all of this is that there's nothing about angular momentum or torque in the code I wrote-- you can look at the source on GlowScript and confirm that. It's all plain vanilla forces and linear momentum. The angular momentum stuff just happens naturally. I think that's pretty awesome. This kind of point tends to be mostly lost on students in the intro class, alas--I've done something similar with energy, which utterly failed to draw a reaction--but then that's why I have this blog...
And there's the latest fun-with-VPython activity. Which also serves as a remember-how-to-do-VPython activity, because next Monday I'll start teaching two sections of intro mechanics again, for the first time in a while, and I was in need of a fun refresher.

Is there a short explanation of *why* angular momentum just naturally falls out of the plain forces+linear momentum description? I've been told this, but it's never really "gelled" for me.
On the Baader-Meinhof phenomenon front, I just watched the MinutePhysics video on angular momentum (www.youtube.com/watch?v=iWSu6U0Ujs8) and one thing they said that I found interesting was that angular momentum always exists, even if you don't have anything actually rotating. (It makes sense, but I never really thought of it that way.)
"Angular momentum is very different than linear momentum" - linear momentum is angular momentum considered as a rotation about the point at infinity (e.g., the limit of angular momentum as the radius goes to infinity, in a direction perpendicular to the motion).
nice post. the video is well done, and a good find.
RM said: "On the Baader-Meinhof phenomenon front..." I'm guessing this is some kind of autocorrect, but I'm intrigued as to what it was meant to be. Or did you really mean the terrorist group?
He probably meant this:
http://en.wikipedia.org/wiki/List_of_cognitive_biases#Frequency_illusion
It's an unwieldy nickname for it if you ask me and it's so weird when it happens.
@RM it depends on what sort of 'why' you're looking for. At one level it's symmetry: the laws of motion are rotationally symmetric, so there has to be a conserved quantity associated with rotation. There aren't any other weird conserved quantities in Newtonian mechanics because energy, momentum, and angular momentum take up all the symmetries.
Today's follow-up post might be a partial answer to a very instrumental version of the "why" question, showing how you can get a force that pushes the whole thing to the left out of gravity and rotation.