One of the toughest things to do in science is to figure out -- of all the things that exist in the world -- is which ones are relevant to your problem. Take the Leaning Tower of Pisa, for instance.

Specifically, I wrote about Galileo's famous problem, where you take two cannonballs, one that's 10 lbs and one that's 1 lb, and drop them simultaneously off of the Leaning Tower of Pisa, about 55 meters up.
Perhaps you'll make the simplest model, and say that the only thing that matters is gravity. Perhaps you'll neglect air resistance, friction, the Coriolis forces, wind, horizontal motions, updrafts, and only consider gravity. If you did, what you'd find is that, as long as you drop them from rest at the same time, they will fall at exactly the same rate, and hit the ground at the same exact time.
But in real life, this is not what happens. In real life, we're dropping these balls from a great height (55 meters), and they're falling through air, not a vacuum. If we want to get an accurate model, we need to take into account air resistance in addition to gravity. Air resistance depends on a few things:
- The speed of the ball through the air,
- The density of the air,
- The drag coefficient of the ball,
- The surface area of the ball, and
- The mass of the ball.
For dropping a 1 lb ball and a 10 lb ball of the same material off of this tower, the major differences are the mass and surface area of the ball. How do you know mass matters? Take a wiffleball and a baseball of approximately the same size, and throw them at the same speed.

The baseball will go higher and farther, because the heavier mass makes it harder for the air to stop it. More surface area also makes it easier to stop, which is why a balled-up piece of paper falls much more quickly than a loose sheet of paper.


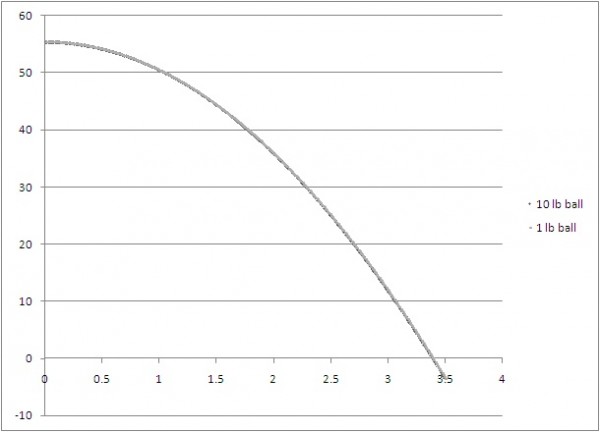
The 10 lb ball would take 3.375 seconds, while the 1 lb ball would take 3.39 seconds. Seems like a tiny difference, right? Practically indiscernible, you say, perhaps looking at the graph above? Well, I've got news for you: your eyes don't see time, they see distance. What would the height differences between these two balls be as they fell?
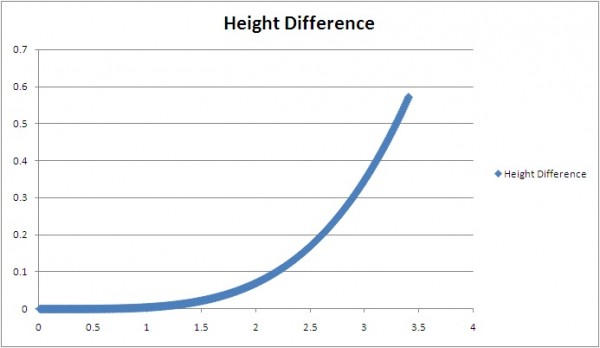
A-ha! The 10 lb ball starts to pull away from the 1 lb ball the farther they fall, so that by time they hit the ground, they're separated by over half a meter (almost 2 feet), a difference that's easy to see!
So no, Galileo never performed this experiment, and if you did, this is pretty much exactly what you would see. And if you like, you can do the math for yourself, and find the same thing. And that's what a good physical model does: it models all of the relevant behavior. If Galileo had done the experiment, what do you suppose he would have concluded about gravity and falling objects? Would physics ever have even developed?

Interesting - I never knew all the details of this alleged Tower of Pisa experiment and I had always assumed that the two objects had radically different masses and the same volume. I suppose we have all been trained to limit every variable we can get at, bar one, and people in the past didn't think like that.
I wish you would have done us another graph showing how much height difference you get with just a variation in mass and air resistance, because I'm allergic to maths after 11pm. Maybe tomorrow.
In reference to the questions at the end, I think Galileo would have realized that air resistance was still messing with the experiment, and that he would have tried a more dense second material (say, copper instead of wood) to reduce the relative effect of drag. Given his understanding of scale factors, he may have also tried varying the size of the spheres to better reduce the effects of drag. If drag is proportional to cross-sectional area and mass to volume, then the solution, as is so often the case, may have been bigger balls.
Addendum: sorry, I forget which version of the story this was, and I couldn't edit my last post. I'd guess that he would indeed try two identically-sized spheres of different materials (like copper and iron). Again, Galileo understood scale factors in other areas, so it's reasonable to think he would have figured out the relevance of scale here, at least qualitatively. So if he had actually done the experiment, I suspect that it ultimately would have advanced his understanding rather than hindering it.
Would this result really be outside the experimental accuracy? Could an observer reliably track two small high speed objects simultaneously? Also the two objects would have to be released together. On your figures, a difference of 15ms between the release of the two different sized balls would result in simultaneous ground strike. How would you verify your release mechanism to this accuracy with mediaeval technology?
It seems to me that detecting, if not directly measuring, the difference in distance of the two objects would simply involve listening for the delay between the two impacts. Anyway, if the experiment would be done, it would be a demonstration for the lay people and he wouldn't have gone up there not knowing exactly what to expect. If there were any reality to the story, then he would have worked all the details out in the first place because just like the apple didn't make Newton realize gravity, dropping cannon balls from the tower isn't how Galileo figured out the squared relationship between time and velocity in falling objects.
I think 'the ancients' thought that the falling speed was proportional to mass, so a 10-kg ball would have been expected to fall ten times as fast as a 1-kg ball, so a difference of 15 ms at impact would have been just as shattering to the paradigm as a simultaneous impact.
Mass is completely irrelevant for air resistance, better known as drag. And the relevant area for calculating drag isn't the _surface_ area, but the _cross-sectional_ or projected area.
Drag is air density times drag coefficient times crossectional area times velocity squared divided by two.
I don't see a mass anywhere in there. Do you?
If you set out to call things bullshit, like you did in your last post, you should make sure that you get things right.
Maschinenbauerin, you say:
If you want to know how an object accelerates towards the ground, you need to consider acceleration, not force. So take your equation for drag force and divide it by mass, and that will give you the acceleration due to drag force. It is highly dependent on mass.
Jesus Christ ...
Drag is a bloody force. How do you convert force to accelaration? Divide by the mass!
Same drag -> different accelarations -> different speeds -> different drags (at the same time - same drag at the same speed, of course).
@ Maschinenbauerin
Actually, in situations of free fall with air resistance, an object accelerates in motion relative to the primary body until air resistance slows the acceleration to a terminal velocity. More massive objects reach a higher terminal velocity than less massive objects, even with idential cross-sectional areas.
Thusly, the effects of air resistance depend on mass, but the forces implied do not. This is why air resistance formulas differ for every object, and Dr. Siegel did not really explain this. Probably because this is a blog post, not a college course. If you ask nicely, maybe he'll explain some basic physics to you so that you can impress someone else with your incomplete grasp of high school level science. But that's just me being snarky.
That's the problem with being a smug pedant. Worst case, you're wrong and you look twice as ignorant. Best case, you're still a dick.
But what if you made both canonballs the same size?
I mean, one solid 10lb and the other one hollow 1lb.
That way they have both the same drag.
If they have different weights, then the air resistance affects them differently, even if they have the same cross-sectional area.
To see this, get a tennis ball and a billiards ball. Put both on a table and blow at each one. They're the same size, but you'll blow the tennis ball a lot farther than the billiards ball.
@ethan:
That's completely right, mass is highly relevant for acceleration. However, it isn't for air resistance itself. People might take what you wrote literally and then think that the force on the balls depends on their mass. If this is a blog only for people who already know the physics, you don't need such a long post with all the explanations, you can just say you calculated the acceleration with taking air resistance into account and that's the result. If it is also meant for people who don't know the physics or who forgot them, then why not be exact? That's what I was trying to point out. Sorry for the harsh tone.
@ sean hogge:
I know the effects of drag, I know mechanics and I know about terminal velocity. So I knew what he probably meant to say. However, there are people out there who don't, and even if it's "just a blog post", I still think one should try to explain things right, especially if it's as easy as in this case. That would have been a matter of one more sentence, maybe two. Or maybe even two more words. But the way it is written, it is misleading. And there are people out there who will believe that air resistance, as a force, is dependant on mass. And I think a science blog should make them know better.
One would expect that the small 1 Lbs ball would fall faster, because of the reduced cross-section, the reduced drag. The effects must partly cancel each other.
@Arthur:
the drag is reduced, but not far enough. Drag increases by radius squared, mass increases by radius to the power of three.
The resulting acceleration is (gravity - drag) divided by mass. So, looking at a single velocity, as drag decreases slower than mass (and, therefor, gravity) with the radius, the gravity/drag ratio decreases with radius. (Not sure if the use of gravity in this case is correct, I use it for "gravitational force", as it's shorter and I'm a bit lazy today)
So for a radius a, let's say drag is 0.1 times gravity, and for a smaller radius b, it's maybe 0.2 times gravity, with the resulting accelerations being 0.9 times g (being gravitational acceleration, see "lazy" above) for the heavier and 0.8 times g for the lighter ball.
To make the balls fall at the same speed, you would need to reduce the drag on the lighter ball even more, for example by making it out of a denser material, so it gets even smaller and the gravity/drag ratio is the same for both balls.
Drag is also proportional to airspeed, so the smaller ball would start falling slighty ahead for a while (due to lower overall drag).
I fear you'll have to write the equations, and plug in the actual values for air resistance, to determinate at which point the 10-lbs cannonball passes the smaller one, Maschin.
We can even envision a case where the bigger ball reaches its terminal velocity first (where the drag balances out the gravitation pull), and the smaller ball reaches a higher terminal velocity (smaller drag, remember ?), so it hits the ground first.
_Arthur: The point where the big ball passes the small ball is a split second after they are released. The smaller ball will fall slower at every single instant in this scenario.
Let's use SI-dimensions: 1 kg and 10 kg, balls made out of steel with a density of 7850 kg/m³, giving the 1 kg ball a radius of 0.031 m and a crossectional area of 0.003 m², and the 10 kg ball 0.067 m and 0.014 m².
Suppose that somehow they fall the first second in a vacuum and after one second with roughly 1 m/s hit the atmosphere. Flow will then be laminar which gives a drag coefficient of roughly 0.45. Density of air at standard conditions is about 1.2 kg/m³. Drag for the two balls is air density times drag coefficient times cross sectional area times velocity squared divided by two, which calculates into 0.00084 N for the 1 kg and 0.0039 N for the 10 kg ball. Substract that from the gravitational force (weight in kg times 9.81).
The resulting force towards the ground is for the 1 kg ball 9.8092 N, resulting in an acceleration of 9.8092 m/s². Resulting force for the 10 kg ball: 98.096 m/s, acceleration: 9.8096 m/s². More than for the 1 kg ball.
The lower the velocity you choose, the smaller the difference, but the acceleration on the bigger ball will always be higher than on the smaller ball.
And no, for both balls having the same density, the terminal velocity will always be higher for the bigger ball. Drag acceleration is proportional to 1/r. smaller r -> higher drag acceleration for a given velocity.
Terminal velocity is when drag acceleration = gravitational acceleration (9.81 m/s²), so when a smaller ball has reached a drag acceleration of 9.81 m/s², the same velocity will lead to a smaller drag acceleration for a bigger ball, so it can reach a higher velocity.
The only chance to make the smaller ball fall faster than the bigger ball would be using aerodynamic tricks to reduce the drag coefficient on the smaller ball.
Since we're being smug pedants, shouldn't we take issue with your significant figures?
Oh, and the fact that you're reducing an expository effort into a mathematical explanation, the antithesis of the entire effort of this post.
Oh, and the fact that since when you speak of "air resistance" you can be addressing either the forces or the effects, and without specification, correctness cannot be accurately addressed.
I don't disagree with what you're saying, for the most part, don't get me wrong. It's just that you've got a lovely model for the trees that doesn't explain the forest.
So what's wrong with my significant figures, did I miscalculate anything?
In my first comment, I just wanted to point out that saying that air resistance depends on mass is misleading. I should have formulated it differently, yes. The comment where I did the calculations was a response to Arthur, who a) wanted an equation and b) gave the impression he thought that the smaller ball would fall faster at the start. It seemed he didn't get it through the expository effort, so I gave the calculation as an addition, thinking this might be clearer.
Regarding air resistance meaning the effects: I never used "air resistance" for "the effects of air resistance" and I don't think I have ever heard or seen it used in this way before. To me, air resistance always meant the forces, never the effects.
What bothers me most with "air resistance depending on mass" is this:
I don't know enough about astrophysics to judge how correct, exact or unambiguous the things are that Ethan writes about that topic. I know, however, enough about fluid dynamics to know that drag (and that's how I interpret "air resistance") doesn't depend on mass, still the conclusion of the post is correct. So what about the posts that I can't judge because I don't know enough in advance? Will he do the same? Use a phrase that means one distinct thing for me (and my dictionary) but means something similar but not quite the same for him? Can I rely only on the conclusions being correct or can I also rely on the way to the conclusions being described in a way that's not easy to misunderstand?
To stay within the forest metaphor: If someone tells me it's a forest consisting of beech and oak trees, I'd like to know which is the beech and which is the oak and how to tell them apart.
I still don't get it.
According to your drag computations (good job),
The small ball will accelerate at g - 0.00084 N
The big ball will accelerate at g - 0.0039 N
So, the same force applies downwards, but the small ball has a smaller drag force in the direction opposite in the movement.
It ought to accelerate faster, then, no ?
I'm confused.
Because you have written Acceleration = (Acceleration due to gravity) - (drag FORCE)
You should have:
Acceleration = (Acceleration due to gravity) - (Acceleration due to drag)
so 0.00039 not 0.0039 for the big ball
Arthur: You're mixing two different things here. g is an acceleration, 0.00084 N isn't, it's a force. To get the acceleration from a force, you have to divide by mass.
So the small ball accelerates by g- 0.00084N/1kg, or g-0.00084 m/s².
And the big ball accelerates by g - 0.0039N/10kg, or g-0.00039 m/s².
The drag force on the smaller ball is smaller, by a factor of roughly 5. However, the mass is smaller, too, by a factor of 10, so the resulting acceleration due to drag is bigger (by a factor of 2).
@sean: See, I cut down my pedantry, I didn't tell him that "g" is "grammes" in SI dimensions ;)
Thanks, I'm less confused, now.
I myself am a fan of pedantry on the whole. It's just that one must wrap it up in a bit of self-effacement or at least a touch of over-politeness to make it palatable to those who do not share the malady. So I've learned the hard way.
I already admitted that the wording of my first comment, ahem, wasn't chosen wisely. The next time I tell someone they're wrong or not quite correct, I'll try to put a bit of sugar on it. For now, I'll just drink some tea with consensed milk. ;)
you have absolutely no clue what you are talking about i am a scientist and i should know what i am talking about! You are entirely wrong! Gravity and physics have nothing to do with it, but they have everything to do with it! And you could not kick down the leaning tower of pisa in a picture, and the guards would not even let you drop balls off of the leaning tower of pisa, you would get arrested! Im also italian. You should get sued for giving out false information because if someone were to use this information, they would get in trouble because it is wrong.The person who got in trouble could give out your name and then you would be arrested for false information. You owuldnt want that would you? I know i wouldnt and i have enough money to pay for all the bills for being arrested. My name is Fritz Haber, and if you would like to contact me, email me @ finch.casey@yahoo.com
i like this website because it shows the scientific skills of simple things also the picture with the leaning tower of pisa is really clever;)
Galileo never actually conducted his gravitational experiments at the leaning tower of Pisa... it is a made up story... he figured the thing out purely hypothetically.
...and all this time I thought it was the Leaning Tower Of Pizza. Thanks for the clarification. I had assumed he was dropping anchovies and pepperoni slices off the thing.
I have few questions (pardon me for my bad English),
1. why you gave us the height difference graph to explain the changes in distance between the two balls when they hit the ground? (at first i thought that the height difference graph is to explain about the time difference between two balls until they hit the ground)
2. "The 10 lb ball starts to pull away from the 1 lb ball the farther they fall, so that by time they hit the ground..." ---> is that mean that 10 lb ball move more far away from starting point it was thrown than 1 lb ball from starting point?
for example : 10 lb move 0,3 m and 1 lb move 0,1 m ?
why can this happen? is it really because the air resistant? because i think direction of air resistance is the opposite direction of the gravity (drag force). i'm confused now.... please help me to understand..
3. what for is the first graph? what it explains? is it not the graph that tell us the path of free fall and the projectile path of "parabolic trajectory"?
thank you very much
I have a few questions for you but pardon me for my bad English.
1) why you give us the height difference graph to explain the change in distance between the two balls when they hit the ground? at first i thought that the graph is to explain about the time difference between to balls (with air resistance) until they hit the ground.
2) "The 10 lb ball starts to pull away from the 1 lb ball the farther they fall, so that by time they hit the ground.." --> is that mean that 10 lb ball move farther than the 1 lb ball from their starting point ? for example : 10 lb ball move 0.4 m and 1 lb ball move 0,1 m?
why this happen? is it really because the air resistance? because i think direction of air resistance is the opposite direction of the gravity (drag force) it means that it will affect the position on y axis direction and not the x axis.
i'm confused now, please help me to understand..
3) what for is the first graph? what is explain? is it not the graph that tell us the path of free fall (left) and the projectile path pf "parabolic trajectory" (right side, and it means they have a direction from the start and because of that they make a parabolic curve because of the gravity)
thank you very much.....
The 10lb ball has more mass per unit surface area, therefore the frictional force is less of a retardation to the falling speed of that ball compared to the 1lb ball, ray.
Do the experiment on the moon, with practically no atmosphere, and the difference doesn't appear.
i see. i think i misunderstood about this sentences >> so that by time they hit the ground, they’re separated by over half a meter (almost 2 feet)<< i thought it was about the distance at the end of their fall on the ground (x axis) :D
@ray
separated over half a meter VERTICALLY. Meaning the heavier ball reaches the ground earlier. NOT that it falls more than half a meter AWAY (horizontally) from the lighter ball.