"I saw for the first time the earth's shape. I could easily see the shores of continents, islands, great rivers, folds of the terrain, large bodies of water. The horizon is dark blue, smoothly turning to black. . . the feelings which filled me I can express with one word--joy." -Yuri Gagarin
It takes a tremendous amount of energy to do any type of heavy lifting, and the most extreme example of this is lifting something all the way up off of the Earth, out of the atmosphere, and into space!
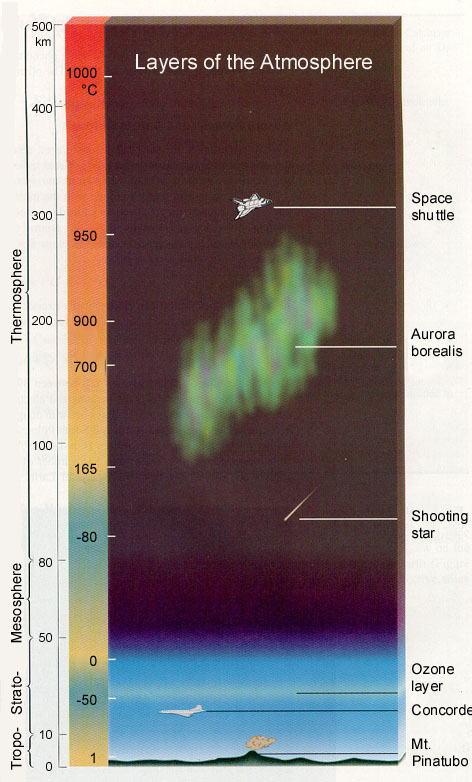
And once you're up there, at least 300 km above the Earth's surface, the sights you've got are bound to be absolutely amazing! For example, if you took the US Space Shuttle up, you'd likely dock with the International Space Station, and get to see something as breathtaking as this:

But gravity is a funny thing. The same force that pulls the Moon into our planet's orbit is trying to pull your orbiting body (and whatever spacecraft it's inside) back towards Earth.

But while the Moon is 384,000 km away from the center of the Earth and takes about four weeks to orbit the Earth, these man-made satellites and space vehicles, at an altitude of around 300 km, are only 6,700 km away from the center of the Earth.
But one of the incredible things that our laws of gravity tells us is that, no matter what distance you are away from any mass, there's only one speed that will keep you moving in a stable, circular orbit!
Any guesses as to what that speed is at the altitude of the International Space Station?
It turns out that you need to travel at a whopping 27,700 km/hr (~17,200 mph) to stay in orbit around the Earth; any slower and you'll fall back down!
But let's take a look at the Earth itself. Although it's a pretty big place, it's only about 40,000 km all the way around; even at an altitude of 300 km, that makes an orbit of only about 42,000 km all the way around!
This means that it only takes about 90 minutes to make a complete orbit of the Earth, or, in Little Prince terms, you get about 16 sunsets per day.

What would it look like, if you were up on the ISS, as you went from Sunset to Sunrise, and got to look at the Earth from space during an entire 40-minute night?
Well, thanks to astronaut Don Pettit, who took a series of images every 15 seconds and stitched it together into a video of one "night" on the ISS, we can see for ourselves!
And, from up in low-Earth orbit, astronauts get to see this sixteen times a day, speeding at over 27,000 km/hr. Pretty amazing stuff; and thanks to NASA's Solar Dynamics Observatory for posting the video!


Pretty pictures :)
Something that bugs me is the term "micro-gravity."
I understand that, on the ISS for example, you are still well within the Earth's gravitationl influence (that's why you are falling), but if you are in freefall, you are effectively weightless, yes?
So, what is "micro-gravity"?
From what I have read, microgravity is simply free fall within a gravitational field. I guess its called that simply because there are always residual acceleration present so you can't really call it 0g. My 2cents....
Those temperatures in the first diagram threw me for a loop (the shuttle orbits in 950degC?!). Oh yeah, the atoms are fast but there aren't enough of them to hit you and transfer any really heat. How about a post on that?
Steve,
Although I only gave it one paragraph, I talked about the analogous problem in the Sun, of the Sun's Corona being a higher temperature than the surface of the Sun.
http://scienceblogs.com/startswithabang/2010/07/whats_the_most_fundamen…
And your explanation is pretty good, too.
I am curious about the "one speed" to keep you in orbit at a particular altitude. Is there an explanation or formula to figure out the speed?
Waydude:
Sure. That's the speed when the centrifugal (or centripetal, if you insist) force is strong enough to counter-act the gravity.
So the equation is: v^2/r * m = G*m*M/r^2
m is the mass of your spacecraft, r is the radius from the Earth's center.
v^2/r is the centrigugal acceleration, so v^2/r * m is the centrifugal force.
M is the mass of the Earth, G is the gravitational constant.
G*m*M/r^2 is the Newton's gravity law.
So simplifying and solving this equation, we get: v = sqrt(G*M/r) - note, that the speed actually doesn't depend on your spacecraft's mass.
Substituting numerical values:
G=6,67*10^-11 N(m/kg)^2
M=5.9736*10^24 kg
r~=6378000 m.
So v = sqrt((6.67*10^-11 * 5.9736*10^24) / (6378000)) ~= 8000 meters per second. Or about 28,000 km/hr.
PS: though there is just one circular orbit for a given radius, there are infinitely mane elliptical orbits.
An even better way to look at this (following Eric Juve) is that "microgravity" is describing what you "feel." And one of the consequences of General Relativity is that you cannot in principle feel gravity if it is sufficiently nearly constant over your whole body. Consider when you walk. When you talk about feeling your weight you feel it in your feet; you are feeling the normal force from the floor, NOT your weight. So if weight is the only force (and the acceleration is the same over your whole body) you do not "feel" any force at all. By consequence, there is not (in the GR sense) any force at all -- if you can't feel a force, it's not there....
Newbie question: what on earth fuels something that goes 27,000 km/h?
Quite commonly, liquid hydrogen and oxygen are used to get into orbit. For rockets, you commonly get the best thrust for the weight if you use light elements that release a lot of energy when they combine. Hydrogen+oxygen are great for this.
Thanks Taxorgian for the explanation of "micro gravity". It really helped me understand the concept better with your description.
Many thanks, Ben W.
Ah, appreciate the responses. I feel less like there was some li'l something that was escaping me.
A question for those who can handle both math and literature. The ISS orbits the Earth in 90 minutes, but we know from Shakespeare that Puck can "...put a girdle 'round the Earth in forty minutes" - or at least he claims he can: the evidence suggests he's more than a bit of a braggart. But taking his boast as fact, how does he do it?
Ur was right impresive but help me concernin d mass of d earth
be coded along with something about 128 bit. With the
How come in every picture we see of "space", either when the moon landings, or any other related picture, like the ISS, or the Shuttles we only see dark space. The Sun is out, there's no pollution, the stars are very bright, right? At least some of them, so..why don't we see the stars? Please don't waste your time with nocuous answers, I'd really like to get a serious answer for this. Thank you.