"Black holes are where God divided by zero." -Stephen Wright
Yesterday, I told you about all the evidence for the Black Hole at the center of our galaxy. In particular, we see multiple stars orbiting a single point that emits no light of any type at all.
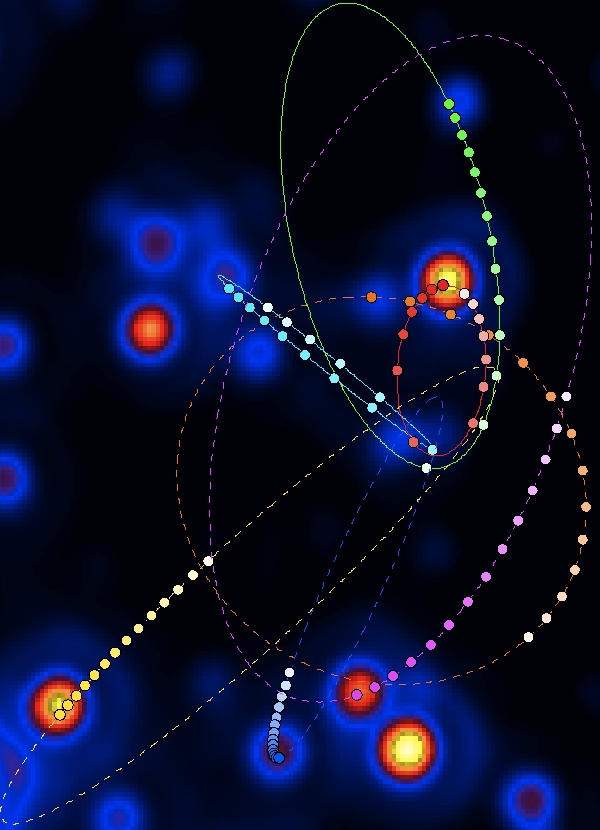
And, perhaps unsurprisingly, the comments became very active. So let's take a look at some of what was said, and let's see what we can further learn about black holes from answering your questions.
I see the stars orbiting on their own orbits, but I mean, all orbits seem quite different to me, there´s no central point they are orbiting around... or is there?
(From wega.)
This is actually a great one! Kepler was the first to figure out that orbits weren't about a central point, but rather in an ellipse-shape, with a mass at one focus of an ellipse.
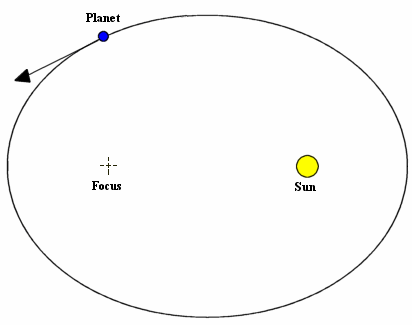
This is true for all planets, comets and asteroids around the Sun, for the Moon around the Earth, and for each of the stars near the galactic center. In fact, if we ask where is this "focus" for each of the ellipses near the galactic center, we remarkably get the same location for each one, below.
So, a lead sphere that was about the diameter of the earth's orbit would fulfil both criteria. [Dense/massive enough and dark.]
So the question is - what measurements have we taken that would invalidate this 'big lead ball' model?
Sure - a big lead ball might not fit our current model of stellar formation ... but I'm interested in whether it contradicts our measurements?
(From Mac.)
There are two surprising problems with this. First off, there's a maximum size that something that doesn't emit light can have, and it isn't given by the density of lead. As planets get more massive, they get bigger. Earth is bigger than Mars, Uranus is bigger than the Earth, Saturn is bigger than Uranus, and Jupiter is bigger than Saturn.
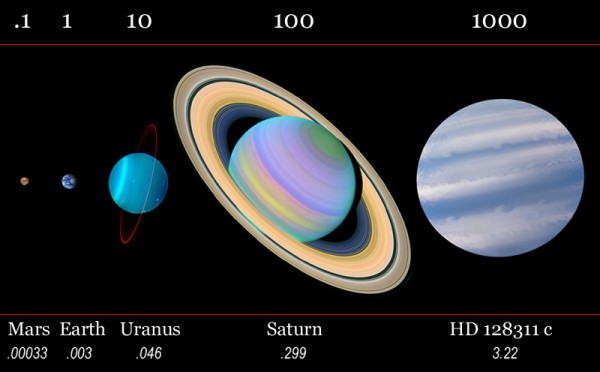
But not by that much! Jupiter is about 3 times as massive as Saturn, but only about 15% bigger! What's going on?
As you get more and more mass together, gravity starts working its magic, and starts compressing the atoms at the center. Bodies much more massive than Jupiter will actually start to shrink in size, and will compress! By the time you get up to about a Solar Mass of lead, you're talking about something around the size of the Earth, similar to a white dwarf star.

But even white dwarfs have a limit. You get about 40% more massive than our Sun in a white dwarf, and the atoms can't stand up to the intense gravitational pressure, and they collapse. (This limit is known as the Chandrasekhar mass limit.)
But we can go even farther! Even if you took a Mercury's-orbit-sized region of space and filled it with a sphere of lead, you can calculate what the escape velocity would be. Guess what you find?

Yup. It's bigger than the speed of light, which means you'd get a black hole anyway!
am also quite unconvinced that mathematical artifacts of General Relativity (=singularities) trump Quantum Mechanics (discreteness of space-time rules out singularities). Maybe Ethan could give us the view of an astrophysicist on this?
(From msironen.)
Technical time; look out, folks! There are a bunch of different types of energy in the Universe. Matter, radiation, and what we call "vacuum energy", which is the same stuff we believe dark energy is made out of. If, when you try to collapse to a singularity, you start producing vacuum energy, you can avoid the mathematical "inevitability" of a singularity. See, for instance, this wikipedia page.
You don't have to go to the galacatic center. The blue giant star HDE 226868 is much closer, and it is also orbiting a dark object much more massive then any neutron star can get. And it coincides with the position of a strong X-ray source.
(From Birger Johansson.)
Okay, check this out.

Cygnus X-1, to which Birger refers, is an 8.7 solar mass object, emitting X-rays, and with another, visible star orbiting it. It is too dense and doesn't have the right properties to be either a white dwarf or a neutron star, and appears to be a black hole with an event horizon of radius 26 km. This system, discovered in 1964, was the subject of a famous bet between Kip Thorne and Stephen Hawking, about whether it was a black hole or not. Hawking, loser of the bet, conceded in 1990 that it was a black hole.
I thought the accretion disks of black holes would be quite bright (including in visible light). Shouldn't we see that?
(From AJKamper.)
Brightness is relative.

Compared to the black hole itself, sure the accretion disk is relatively bright. But the actual amount of light coming from it? Unless you've got something like a super-duper-massive one, like a quasar,

you're not going to "see" anything. (Image credit: here.) Most of the emitted "light" isn't in the visible part of the spectrum, unfortunately. But the radio waves (quasars stand for quasi-stellar-radio-sources) and the x-rays are, in fact, how we detect these guys in the first place!
Thanks for some great comments! I'm sure you'll have more for me, and I hope I've gotten to answer some of the more interesting ones!


I would love to turn the photo of the stars orbiting a single point at the center of our galaxy into a problem for my physics students (perhaps even trying to have them model it in vpython). Is it possible for you to tell me where you got the photo, and perhaps get some measurements/data to go along with it?
Here is an 70-frame animated gif of some of the infrared observations. Very cool stuff.
Brad
The wiki on Sagittarius A* states "the radio source is not centered on the hole and arise from a region close to the event horizon possibly in the accretion disc or a relativistic jet of material ejected from the disc"
Is it possible to correlate the orbiting stars and the radio emissions?
John - I believe the observations are done at Keck by the galactic center group out of UCLA.
http://www.astro.ucla.edu/~ghezgroup/gc/?
To be more explicit;
The Wiki states;
"S2 (also known as S0â2) is a star that is located close to the radio source Sagittarius A*, orbiting it with an orbital period of 15.56 ± 0.35 years and a pericenter distance of 17 light hours (18 Tm). Given a recent estimate of 3.7 million solar masses for the mass of Sagittarius A*, the maximum gravitational acceleration experienced by S2 at the pericenter of its orbit would be about 1.5 m/s2 or almost one-sixth of Earth's surface gravity".
Do we see a spike in radio emissions as a orbiting star passes the BH?
Can we deduce a lag time?
Can we derive the specific accretion rate from radio emissions, the accretion lag time, the mass and how far the specific star passes by the specified BH?
What I'm driving at here is, is a BH of a specific size only capable to accrete matter at a specific rate under normal circumstances and what happens when an oncoming star collides with the BH (does it exhibit a feeding frenzy,is that even possible), versus being stripped of it's mass a little at a time on each pass.
Is there an equilibrium to accretion?
Are the radio emissions steady?
Can we tell if our BH has a specific accretion/consumption rate?
What do you think about the idea that black holes are unfalsifiable, because they cannot be directly observed, and so are unscientific?
Also, as a wise man (see link above) once asked: if promoting black holes cause people to read the Bible less, would you want to promote them?
mad the swine;
You can't see the air you breathe either(hopefully)but you can detect it in other ways.
Most wise men only have to read a book once.
What do you mean we can't directly observe them? We can't directly observe many things, like electrons and distant galaxies and x-rays and nuclei and Mars and so on. It's no criticism to say something can't be "directly observed."
The real question is whether they can be falsified. In principle, of course: realistic solutions of general relativity make very specific quantitative and qualitative predictions about the nature of black holes. If we could cruise the universe at our leisure looking for them, or create stars in some stellar laboratory and observe them throughout their lifetimes, then we would have ample opportunity to falsify the predictions of general relativity.
In practice, the answer is a limited yes: in a general sense, general relativistic models predict that once matter reaches a certain density, it will collapse. Inevitably. So, for instance, we should find no neutron stars with masses greater than about 5M_sun. We should also, given this hypothesis, expect there to be objects with gravitational influences which do not radiate at all, or whose related spectra fit that of only accretion disk models (not, say, neutron star models).
(Heuristically, the great additional experimental and observational evidence for general relativity, such as gravitational lensing, frame dragging, accurate orbit predictions, and so forth, also leads us to place more weight on its untested predictions.)
Finding even indirect evidence for black holes is very hard, and ruling out alternatives like neutron stars is even harder. Astronomical evidence is necessarily purely observational and dynamic in a way that experimental evidence is not. This is why the very existence of black holes was hotly debated and contested within the physical community for the better part of a century --- the first models predicting black holes were proposed during World War I, but (as in the blog post) even leading theorists like Hawking didn't readily concede that there was concrete observational evidence for the existence of black holes until a couple of decades ago.
First off, thanks for answering my question Ethan (and Sphere Coupler, who was maybe a bit more technical than I was ready for)! That had been bugging me for a while.
Second, I don't get how measuring the gravitation of something wouldn't be a measurement. Why are EM forces "observations" but not gravitational forces? Doesn't make sense. Now if someone wanted to claim that the question of whether a singularity is inside a black hole isn't scientific, that would make more sense. However, even in that instance a theory that accurately described the universe, made falsifiable predictions, and also as a matter of course made predictions about what happens inside a black hole would certainly be scientific, even though the predictions it made wouldn't really be of the singularity itself.
OK, I've ans. some of my own question, The Schwarzschild radius, spin, ang momentum dictates the amount of intake, anything above that amount creates a flare (as observed by UCLA with infrared)and if the amount of incoming is greatly excessive then Jets are formed and actually help inhibit the feeding frenzy(at least where the focal point of the jets are concerned).Our galactic center is currently in a mild accretion era perhaps ADAF yet in approximately 10 million years there is a group of stars expected to accrete and possibly fire up the jets.
The one thing that is truly wild about black holes within a galaxy is that when two AGN approach each other, the BH accretion rate can possibly increase to a point where these jets are formed, and these jets of extreme energy are highly destructive to any matter that crosses it's path.
So in effect two approaching AGN battle it out with these jet/swords and brute force of mass. The one with greater mass or perhaps the best line of attack wins and in this case...winner take all!
The question being if the Milky Way being the smaller structure would naturally turn 90 degrees to meet Andromeda with an active jet.
It's truly amazing how we as humans have mirrored the waring features of our own larger scale environment, kinda implies fractal geometry.
A black hole can also be described as a gravitational lens that curves inwardly upon itself.
This makes a black hole an observational artifact to those of us not in it. To those in it, it just is, and is all.
What does it mean when you say that light can't escape from a black hole? I thought that the speed of light was constant in all inertial reference frames? How is the light stopped?
I watched an awesome youtube video explaining vacuum energy the other day.
http://www.youtube.com/watch?v=KsepwggEjms
Completely blew my mind.
The key to your answer is this: ... in all inertial reference frames. The reference frame of an observer sitting outside the black hole watching things fall in is most definitely not inertial. But it gets weirder.
Remember that special relativity can be summed up as: space and time conspire to make the speed of light constant for all inertial frames. So, say we're watching some guy fall into a black hole and he's sending us pulses of light every second. In his frame, which is inertial, he keeps shooting off a pulse of light every second until the tidal forces tear him into a mist of subatomic particles. He doesn't know an event horizon exists: he falls right into the singularity, or whatever's behind the event horizon.
Our frame, however, is not inertial: we're accelerating upward. In our time, the closer our poor buddy gets to the event horizon, the longer it takes light to escape. Do we perceive this as the speed of light slowing down? No -- we perceive it as his time slowing down. The light is also greatly redshifted since it loses energy climbing out of the gravitational well (think of it as being stretched out). So instead of every second, we see the pulses, dimmer and dimmer, spaced out more and more. Our pal slowly approaches the event horizon and merges with it until our signal of him is fuzzily gone.
Ultimately, light is not stopped. However, space and time's conspiracy to preserve c creates the existence of the event horizon. Matter that passes through is shredded and destroyed. Matter that doesn't never sees anything pass through.
The light doesn't stop in a black hole, it travels in a curved path that stays within the event horizon but its speed is constant.
Neal's answer to Tim misses an important detail: in general relativity, an object orbiting under the influence of gravity, with no source of propulsion, is in an inertial reference frame. What actually happens is that mass warps spacetime, so that while the speed of the light is the same for all observers, the standards for length and time in one frame are not seen as the same in the other frame. It's a generalization of what happens in special relativity, where the speed of light remains unchanged but my meter and second won't look like a meter and a second to somebody in a frame moving with respect to mine (particularly if the relative speed is a noticeable fraction of the speed of light). As long as the one observer stays at least three Schwarzschild radii away from the black hole (that is the radius of the smallest stable circular orbit), he can remain in an inertial frame and watch the other fall in.
Inside the event horizon, light continues to move at the speed of light, but all forward paths in spacetime lead to the singularity, even along the light cone. This observer might be able to receive messages from outside the event horizon, but he cannot communicate to someone outside the event horizon.
Something is not right: How can gravity overcome the quantum exclusion principle for fermions (like in neutron stars) or is there something I don't understand? The explanation "gravity is just too strong" is not good enough for me. You would have to consider that neutrons are not fundamental particles but composite particles (or even something completely different like strings or whatever?). There are holes in the theory (no pun intended) that may (or may not) be solved with a quantum-gravitational theory. Even if Hawking and Penrose proved the existence of singularities (just under special circumstances), the theoretical description (not to mention an experimental measurement) remains an unsolved problem.
Thanks, Eric. What does an inertial observer whose proper path does not cross the event horizon observe as another observer falls in?
@Apeiron -- Here's my understanding. With statistical mechanics, you can represent the exclusion principle operating on a fermion gas as pressure that depends on density. Then you calculate the outward force versus the inward force of gravity and see for which densities gravity always wins.
It's not a very enlightening method, but (I, with my undergraduate degree only, understand) it's the best model we've got for making predictions about such exotic situations.
It doesn't help that we can't recreate those phenomena in the lab.
Thank you for answering some of the questions! Fascinating!
Since we only ever observe the stars moving rather than completing orbits, how do we distinguish between a black hole scenario and one in which multiple bodies are simply exerting their gravity on eachother?
@20 (MadScientist): Two points.
(1) We have observed a star (SO-2) complete a full orbit.
(2) I am not sure, but it's a good obvious question so I'm sure the people working on the galactic center have thought about it. My guess is that it either involves n-body simulations or is a clever deduction based on mechanics I'm too rusty to recall at the moment.
The requirement for the very high mass (millions of solar masses) comes from the observed trajectories. For something to be moving at those velocities in a curved path, something has to be causing that path to be curved. Either gravity from a mass (and the mass can be calculated from the orbital dimensions and period) or some kind of rocket. Rockets to move star-sized masses would likely produce other effects that have not been observed. If the millions of solar masses were distributed in the visible (and moving) objects, then the trajectories would show a movement of the center of mass of the system. The center of mass of the system isn't moving very much as star-sized masses orbit it, so it must be massive enough that star-sized masses don't move it that much, it must be many times larger.
I presume there have been Doppler measurements that have shown how deep in the gravitational well the stars have gotten along their trajectories. Those would falsify a rocket hypothesis.
"It's bigger than the speed of light, which means you'd get a black hole anyway!"
That's the thing I never understood about black holes. The argument I see in lay physics books is that 'The escape velocity is higher than the speed of light. Nothing can travel faster than light. Therefore nothing can escape."
That logic is nonsense. 'Escape Velocity' is the velocity a rocket would have to be going WHEN IT SWITCHES ITS ENGINES OFF to be assured of not falling back to earth.
If you keep the engines on you can escape much easier - at a much slower speed. You don't have to reach the misnamed 'escape velocity' at all! (Technically you would just keep going at 1 meter an hour until you have reached the point when 1 m/hr is the escape velocity - but you get my drift. That's why a space elevator would be so cool...)
So I understand that light would never escape from the lead ball (and so it would appear black - even if you shine light on it).
That's not the bit I don't understand. The bit I don't understand is the whole 'event horizon' stuff - why is escape impossible in the normal way ?
(I realise that no physical spaceship would hold together well in that gravity - it's a very hypothetical question.)
Mac
(PS: And yes - I'm not seriously suggesting it's a lead ball! I'm just trying to understand this part of physics)
Mac, I think I can answer that for you.
Gravity produces a negative acceleration. If you are on a planet where the negative acceleration is 10 m/sec^2 (a bit more than Earth's gravity), to move up one meter per second, you would have to be accelerating by 11 meters per second per second. That is, every second, you would have to increase your velocity by 11 meters/sec.
So what happens in a black hole? If light cannot escape it, the negative acceleration is beyond c at any point within the event horizon. If it takes 10 m/s^2 plus one to get out of a slightly more than Earth grvity well, it would take at least c+1 to get out of a black hole.
I-am-not-a-physicist (yet), but I think I'm right. Will the scientists please correct me if I'm off?
@Mac#23: That's not how gravity and escape velocity work at all. Your velocity will determine the distance (or orbit) you can achieve from a body. If you do not reach at least that velocity (well, speed actually) you will not be in a stable orbit and you will come crashing back down. Low earth orbit satellites (including the ISS) still experience enough air friction to be slowed down and they need to fire onboard rockets now and then to maintain their orbit.
So, a lead ball with mass M = 1.0*Msun would have a radius of about 5800 km... how does one compute that?
What's the actual formula that relates mass and radius of a body in hydrostatic equilibrium? Does the result depend on the chemical composition of the body?
@Helen (#24)
Sorry - that doesn't work. For a start, you are mixing units. You can't say 'acceleration is beyond a certain velocity' - anymore than you can say 'you can't reach a speed more than 3 seconds'.
@Mad (#25)
I appreciate that. So why can't you build a hypothetical ladder and climb out off the hypothetical lead ball? What is the magic of 'the event horizon' that prevents this?
@Algernon (#26)
The inputs to the equation are:
1. The density of the lead. (11340 kg / cubic meter)
2. The mass of the object (1 million solar masses)
Density = Mass / Volume
ie: Volume = Mass /density
Then from volume use the formula for a sphere to convert it to radius:
Volume = (4 * PI * r^3) / 3
ie: r = cube root ( (Volume) * (3 / (4 * PI)) )
ie: r = cube root ( (Mass/Density) * (3 / (4 * PI)) )
You can just type the formula direct into google and let it sort it out:
Type in (without the square brackets):
[ cube root of ((1 million x 1 solar mass) / (11340 kg per cubic metre) * (3 / (4 * PI))) in km]
This gives a reading of 35 million km.
(I think the answer is right - I often stuff up the maths so definitely check it yourself.)
Mac - in regards to your question of #23. You have to stop thinking in Newtonian terms and start thinking relativistically. Inside an event horizon all null and timelike geodesics lead to the singularity. The speed of light limits your speed: your velocity can never point outside of the local light cone, no matter how much you accelerate. If exp of the light cone at your point is going to the singularity, then so are you, no matter how hard you accelerate.
Heuristically, think of space and time as flowing into the singularity. (There is a way to make this precise, but I don't know it.) The local acceleration is related to how "fast" spacetime is flowing. Inside the event horizon, it goes so fast that light itself is pulled in, so there's no way you in your rocket can get out.
Again, that's heuristic. The moral: think relativistically! :)
PS- I seem to recall from Thorne's book many years ago that at the event horizons of very large black holes tidal forces are quite low. A spaceship could pass through and not notice for some time ... but by then it would be too late!
Interesting facts
however,several statements seems not so lucid
I'm still not happy with that original diagram. If you plot lines across the centres of the ellipses, ie through the foci, they should meet at the black hole, or at least at the common centre of gravity. But they don't appear to do this. They seem to be centred on several places. In particular, the green and light blue stars don't seem to share a common focus.
#17: The work done by the collapsing outer layers bumps the fermions composing the degenerate stellar material into higher and higher energy states (i.e. the stuff gets REALLY HOT) so Pauli exclusion is not violated.
arama motorlarinda en iyi yerlere gelmek istiyoruz Alınan bilgiye göre, Dörtyolâun Yeniyurt köyü yakınlarındaki BotaÅ tesisinde, 150 bin varil ham petrolün bulunduÄu akaryakıt tankına yıldırım düÅtü.
Tesis çalıÅanlarının müdahalesiyle kontrol altına alınmaya çalıÅan yangın, kısa sürede büyüdü.
Yangına Dörtyol, Ä°skenderun, Erzin ve Adanaânın Ceyhan ilçe belediyesi itfaiye ekipleri müdahale etti
mad the swine - that link points back to Conservapedia, a cesspool of anti-science nonsense. They claim that only directly observable measurements are "true science" so they can continue to vilify evolution. They also maintain that Relativity is false, so they deny the _indirect_ evidence for black holes, too.
The very worst part about it is that an awful lot of children (many home-schooled) use that collection of lies a primary reference.
Mac (#23) you're right that merely saying that an escape velocity exceeds the speed of light isn't a full explanation, because in a Newtonian context a rocket would still be able to escape.
As Neal (#28) pointed out, the real explanation requires us to shift to relativity theory (and its unification of space and time into a four-dimensional spacetime).
It might be helpful here to set aside the question of black holes for a moment, and just focus on the fact that Special Relativity tells us that nothing can go faster than light. From a Newtonian context, this would seem like nonsense. After all, if you're going 90% the speed what could prevent you from accelerating to double your speed? Further, speed itself is always relative, so if you have two objects approaching each other, each at 90% the speed of light (according to you), then clearly (says Newton) the one object will be going 180% the speed of light relative to the other.
Of course, Einstein taught us that this obvious and straight-forward reasoning fails because space and time are entwined in a non-Newtonian way. The objects in this situation are traveling less than the speed of light even relative to each other. And it is impossible to accelerate beyond the speed of light. Period. It doesn't matter how fast you're going, or what reference frame you choose. The geometry of spacetime says no physical acceleration can accelerate a mass beyond the speed of light.
This likewise rules out the possibility of a perfectly rigid object. In the Newtonian context it would make sense to suppose that you could have a perfectly rigid pole, and then tapping on one end with a hammer would instantaneously move the far end. You could use this set up to send instant messages in Morse code. But Relativity theory rules that out. All disturbances have to travel at or below the speed of light.
Now let's consider black holes (this relies on General Relativity, which accounts for gravity). Relativistically, when we say light itself is not going fast enough to escape the black hole's gravitational pull (i.e., the distortion in spacetime it causes), we see that nothing whatsoever can escape. It's impossible to go faster than light, and light itself is too slow to get out.
Likewise, it would be impossible for any body to remain at rest in the black hole (i.e., not fall inward), because this would be like having a rigid pole that could be used to send hammer-tap signals faster than light. So, according to Relativity Theory, if you did have a lead ball so compact that its escape velocity exceeded that of light, it would have to collapse under its own weight -- nothing could stop it. Likewise, there there can be no ladder to climb out of a black hole; the rigidity required is ruled out by the very nature of spacetime postulated by Einstein.
can earth go in side one????????????
if there are 4 forms of mater! When a black hole consumes anything it must resort to a gas! If that is true then it must go somewhere ? Maybe a chamber where all black holes all converge , when all mater is consumed it creates a big bang? What do you think?????