"If I have ever made any valuable discoveries, it has been due more to patient attention, than to any other talent." -Isaac Newton
Born the year Galileo died, Isaac Newton is one of the most revered figures in all of physics.

In addition to the work he did on optics, planetary motion and gravitation, Newton is also famous for his three laws of motion, which -- even today -- apply very well to every particle in the Universe. They are:

Law #1: An object at rest will remain at rest, and an object in motion will remain in motion, unless acted upon by an outside force.
What does this mean? It means that, whatever velocity something starts out with, that velocity -- both speed and direction -- will not change unless something else in the Universe exerts a force on it. In other words, any object can't change its motion on its own; it needs something else to push, pull, or otherwise exert a force on it.

Law #2: The time rate of change of momentum of any object is equal to the net external force acting upon it.
This law is often -- including on wikipedia -- misstated as force equals mass times acceleration, or F = ma. This is often, but not universally true, as we'll see below. But this is very important, because it tells us not just that something changes its motion if something pushes, pulls, or otherwise exerts a force on it, but it tells us how that motion changes!
And finally...
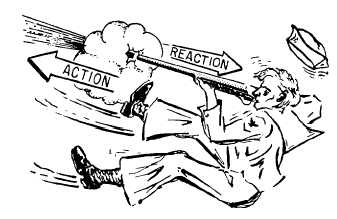
Law #3: For every action, there is an equal and opposite reaction.
What did Newton mean when he said action? He meant -- at any instant -- force, or, over time, a change in momentum. So if you punch your enemy in the face...

...your fist exerts a force on his face, and his face exerts an equal and opposite force on you fist. And in the prior example, if you use a small gunpowder explosion to change the momentum of a bullet, the equal and opposite reaction is the equal and opposite change in momentum of you holding the gun, known commonly as recoil.
It pays to be aware of this.
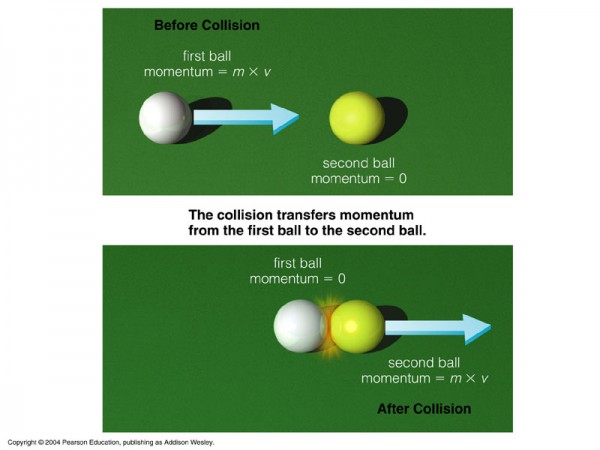
So do we really need all three of Newton's Laws? Think about that first one for a minute. You can be at rest and stay at rest, or you can be in motion and stay in motion. But in either case, there's no external force on you.

You might realize that Newton's 1st Law is a special case of Newton's 2nd Law! So we can combine those two and simply say that the net external force, which can be zero, is the time rate of change of momentum.
But remember, there's that third law, too.

That external force that changes your momentum is coming from somewhere. And there's an equal and opposite force on whatever thing pushes you, and therefore -- by the second law again -- it gets an equal and opposite change in momentum!
So what do we learn from this? Momentum, if you look at all the objects exerting forces on each other, is conserved overall.
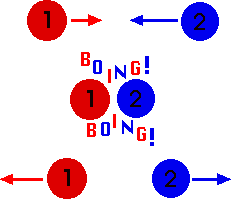
So there's this one concept, the conservation of momentum, that when you combine it with the definition of momentum, gives you all of Newton's Laws.
And one last thing: why do I say that F=ma isn't quite right?

Because when you get close to the speed of light, you can't accelerate up to it, no matter how much force you have!
But you can still increase your momentum, and the time rate of change of momentum is still equal to the net force on you! Does that mean Newton anticipated Einstein's theory of special relativity?
We'll never know, but of all the ways for Newton to phrase his second law, he sure did pick an interesting one!

"If I have seen further it is only by standing on the shoulders of giants."
A genius in so many ways.
I fucking LOVE this blog.
If Sir Isaac Newton had seen a glimpse of special relativity, do you think it would have been well received?
Perhaps he was even smarter than most realise and therefore shared with the people, of that time, just enough to keep them interested and following the right path, without the fear of losing them or running the risk of talking so far above them and being so misunderstood, that being labeled a quack would have been easier.
It happens.
I personally think that Albert Einstein knew what he was doing too, and didn't go too far...He held back just as many do today, for fear that the general public is not ready and slower baby steps are taken.
Like you say "We'll never know"
Just as Newton was correct in 1687, Einstein was (more) correct later on,
Perhaps just as Gustav Kirchhoff was correct in 1860 about black body radiation...someone may be (more) correct, in the future.
I get blasted for saying this sometimes, yet I think it needs said;
"Science is only correct for it's time"
I think that this is accurate...if taken in the proper context.
Thank you for explaining the 3 laws in such a lively and fun way. (unlike my science teacher back in the day) Science is fun after all.
Sphere Coupler:
:-) Perhaps you're getting blasted by the Apostrophe Nazi's [sic]? Sorry!
As Jocelyn Bell Burnell points out: science isn't about finding the truth about the world, it's about understanding the world better. Not really correct or incorrect, just best available.
Even in the nonrelativistic case, F = ma does not always hold. Specifically, if you are talking about a rocket.
Newton's formulation of the Second Law says that F = dp/dt. Substituting p = mv and using the chain rule yields F = m(dv/dt) + v(dm/dt). In most cases the second term is 0, so the whole thing reduces to F = ma (since by definition a = dv/dt). But a rocket is pushing exhaust out the back, so dm/dt is not zero.
Beyaz Saray Sözcüsü Jay Carney, Libyaâdaki Åiddetin durdurulmasına yönelik âaskeri yollar da dahil olmak üzere tüm seçeneklerin masada olduÄunuâ bildirdi. Ãst düzey bir AB yetkilisi de silahlı müdahale konusunda âÃzerinde çalıÅtıÄımız ihtimallerden birisi bu dedi
"If I have seen further it is only by standing on the shoulders of giants."
A genius in so many ways.
Except in grammar.
(farther)
The further/farther distinction, as with many popular rules of English usage (usage, not grammar), is mostly imaginary: http://www.dailywritingtips.com/farther-further-whats-the-difference/
Back on topic -- if you're dealing with rolling balls, then you also have to account for conservation of angular momentum. If you see the harmless-looking words "rolls without slipping" in a physics problem, there's a good chance you need to add an I*omega term to your momentum conservation equations.
meh. that Newton character wasn't so smart: he used to stick needles in his eyes and dabbled in alchemy.
:)
Hi Ethan,
I think it would have been worthwhile to point out that in Newton's time the laws that we know as Newton's 1st and 2nd law were already widely acknowledged and used.
Newton's contribution was to show how the laws of motion could be used to much greater effect than had been achieved up to then. And not only for planetary mechanics. For example, Newton also showed that using the laws of motion and a law for elasticity of air one could derive the speed of sound from first principles. (This reminds me of a later step forwards by Maxwell, deriving the speed of propagation of electromagnetic waves from first principles.)
You suggest that the 1st law can be regarded as a special case of the 2nd law.
I prefer the point of view that the 1st and 2nd law serve distinct purposes.
In effect the 1st law asserts that space is euclidean. It's only when space and time are euclidean that objects in inertial motion travel in straight lines with uniform velocity.
Today we have the general theory of relativity, according to which space and time are not euclidean.
I like to think that Newton sensed that space being euclidean is a non-trivial assumption. I like to think this led to Newton feeling that the laws of motion needed both the 1st and the 2nd law.
Conclusion:
I think it's not a step forward to regard the 1st law as a special case of the 2nd law.
Other than that:
Newtonian mechanics as a discipline is of course as relevant today as it ever was. But I do think the particular way Newton's three laws are formulated is outdated.
I think when newtonian mechanics is taught a modernized set of laws of motion should be used, instead of Newton's formulation.
Eric Lund @7 beat me to it, and I'll second Cleon Teunissen's post, although it might be better to say "It's only when space-time is (locally) flat (or Minkowskian) that objects...".
The notion of an object "at rest" is still often taught as if this were a "natural state of affairs", while something moving (even at constant v) is somehow special. Almost Aristotelian. We don't have to teach the maths of General Relativity to present a more encompassing, accurate and therefore more useful, understanding of the nature of motion to our students. In this, I think Ethan's post is spot on.
I especially liked the last sentence:
I think when newtonian mechanics is taught a modernized set of laws of motion should be used, instead of Newton's formulation.
The standard historical (Newton said so) approach reminds me of the joke pertaining to "Ohm's 3 Laws".
"The standard historical (Newton said so) approach reminds me of the joke pertaining to "Ohm's 3 Laws"."
Except that V=I*Z does break down differently when applied to the 3 passives. :P
Sam C @6
OK,,,,I'll buy that.
It's basically the same as I try to imply, only my statement recognises the building of knowledge of those who came before us.
rob @11
Wait! What?
You mean this IS NOT a standard practice for those in the quest?
*hides needles*
Just joking...of course.
I like the way Tommasso puts this in his well written article in the IOP.
Quote from IOP article 3/1/11
On the road to discovery.
"Like Newton's theory of classical mechanics, which we now understand to be the small-speed approximation of Einstein's theory of relativity"
http://physicsworld.com/cws/article/indepth/45226
I personally feel this defines Newton's laws well to an extent based on the information we have recently discussed in my physics class. However, I am not sure I agree that the 1st law is a special case of the 2nd law. I think these two laws have their own, individual meanings and should not be paired with one another. I am still uncertain as to how F=ma is not always true. If you are you moving towards or away from an object no matter the amount of force exerted, you are still accelerating. Also the farther you go, the more momentum you build up so you would be accelerating. You would be accelerating because you are changing your original velocity. Overall, I feel this article describes Newton's 3 laws fairly well and it gave me a clearer understanding of each.
@Meg #16: Consider the case of an applied torque. Spin a gyroscope, and push perpendicular to the axis of rotation. The gyroscope won't move in the direction of the push, but instead will precess perpendicular to _both_ the direction of the push and the axis of rotation.
For every action there is an equal and opposite re-action.
*That acts on different bodies*.
Quite a important coda.