"The first principle is that you must not fool yourself--and you are the easiest person to fool. So you have to be very careful about that. After you've not fooled yourself, it's easy not to fool other scientists. You just have to be honest in a conventional way after that." -Richard Feynman
Last week, a collaboration of 160 scientists working in Italy wrote a paper claiming that their experiment shows neutrinos traveling faster than the speed of light. Although I wrote up some initial thoughts on the matter, and there are plenty of other excellent takes, we're ready to go into even deeper detail.
First, a little background on the humble neutrino.
Early in the 20th century, physicists learned in great detail how radioactive decay worked. An unstable atomic nucleus would emit some type of particle or radiation, becoming a lower-mass nucleus in the process. Now, if you added up the total energy of the decay products -- the mass and kinetic energy of both the outgoing nucleus and the emitted particle/radiation -- you had better find that it equals the initial energy (from E = mc2) that you started off with!
For two of the three common types of decay -- alpha and gamma decay -- this was, in fact, observed to be true. But for beta decay, the kind shown in the diagram above, there's always energy missing! No less a titan than Neils Bohr considered abandoning the law of conservation of energy on account of this. But Wolfgang Pauli and Enrico Fermi had other ideas.
In the early 1930s, they theorized that there is a new type of particle emitted during beta decay that was very low in mass and electrically neutral: the neutrino.
Because it's uncharged, neutrinos are only detectable through the same nuclear interaction that causes radioactive decay: the weak nuclear force. It took more than two decades to begin detecting neutrinos, due to how mind-bogglingly weak their interactions actually are. It wasn't until 1956 that the first detections -- based on neutrinos (okay, technically antineutrinos) from nuclear reactors -- occurred.
And since then, we've detected naturally occurring neutrinos, from the Sun, from cosmic rays, and from radioactive decays, as well as man-made ones from particle accelerators. The reason I'm telling you all this is because we've been able to conclude, based on this, that of the three types of neutrino -- electron, muon, and tau neutrinos -- that the mass of each of these neutrinos is less than one-millionth the mass of the electron, but still not equal to zero!
So whether these neutrinos are created in stars, in supernovae, by cosmic rays or by particle accelerators, they should move at a speed indistinguishable from the speed of light. Even over distances of thousands of light years. That is, of course, assuming special relativity is right.
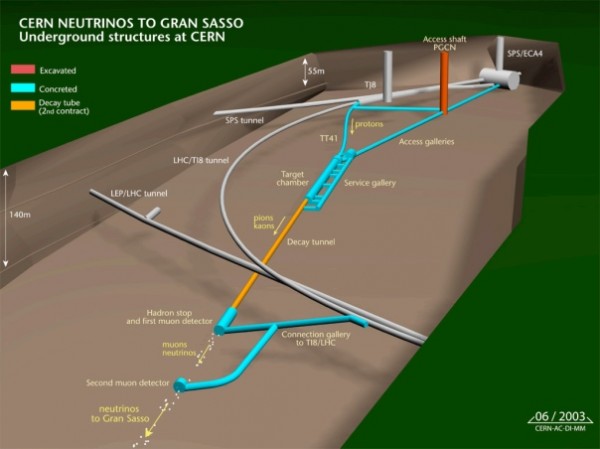
Image credit: the OPERA collaboration's paper, as are all the remaining figures except the ones generated by me.
So, as I told you last week, CERN made a neutrino beam by slamming ultra-high-energy protons into other atoms. This makes a whole slew of unstable particles (mesons), which decay into, among other things, muon neutrinos.
Now, here's where it gets fun. Since they started taking data, CERN's beam has slammed upwards of -- are you ready? -- 100,000,000,000,000,000,000 protons into other atoms to create these neutrinos!
These neutrinos then pass through more than 700 km of Earth before arriving in the neutrino detector. This distance, they claim (with justification), is so well-measured that the uncertainty in it is just 0.20 meters! Over the three years the OPERA experiment has been running, they've finally managed to collect around 16,000 neutrinos, which is a mind-bogglingly small percent -- something like 10-14 % -- of the neutrinos created!
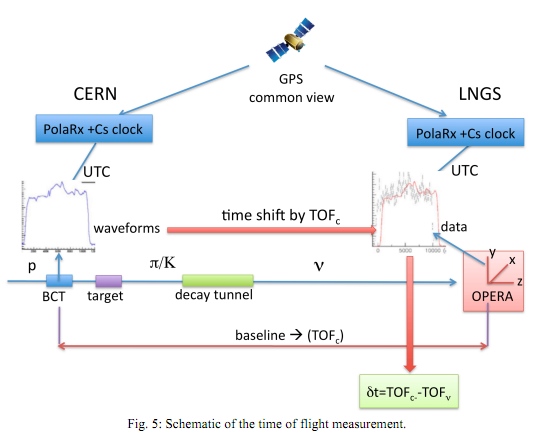
Now, you may ask, how did they conclude that these neutrinos are arriving about 60 nanoseconds too early?
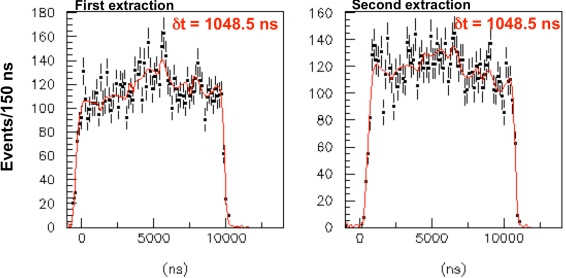
The first thing you go and do is measure all of your initial stuff -- all 1020 protons -- and figure out what you're starting out with. In this case, the protons were created in pulses that lasted for just over 10,000 nanoseconds each, of roughly constant amplitude (but with some variation in there). You sum all the pulses together, and you get the distributions shown below.
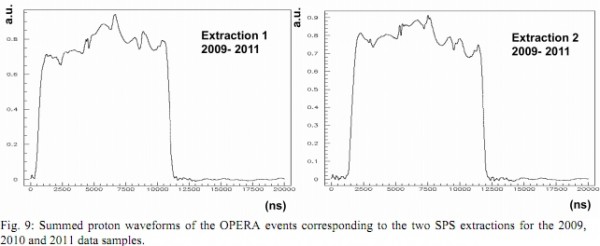
Now, in a perfectly simple, idealized world, you would measure each individual proton and match it up with the neutrino you end up with in your detector. But of course, we can't do that; it's too difficult to detect neutrinos. For example, if you sent one proton at a time, with just 100 nanoseconds in between each proton, you would have to wait thirty years just to detect one neutrino! This will not do, of course, so here's what you do instead.
You take this very precisely measured distance from your proton source to your neutrino detector, divide it by the speed of light, and that would give you the time delay you expect in between what you started with and what you receive. So you go and record the neutrinos you receive, subtract that expected time delay, and let's see what we get!
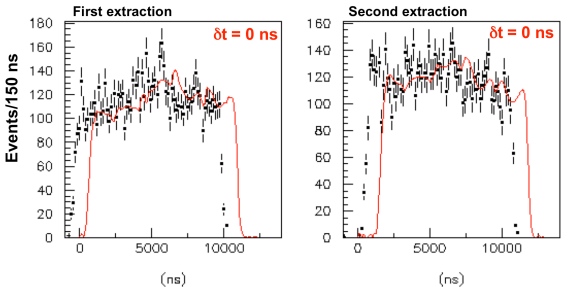
"Oh my," you might exclaim, "this looks terrible!"
And you'd be right, this is a terrible fit! After you re-scale the neutrino amplitude to match the initial proton amplitude, you'd expect a much better match than this. But there's a good reason that this is a terrible fit: your detector doesn't detect things instantaneously!
So you need to understand to extraordinary precision and accuracy what your detector is doing at every stage in the detection process. And the OPERA team does this, and comes up with an expected additional delay, due to their equipment, of 988 nanoseconds. They also try to quantify the uncertainty in that prediction -- what we call systematic error -- by identifying all the different sources of their measurement uncertainty. Here's what they come up with.
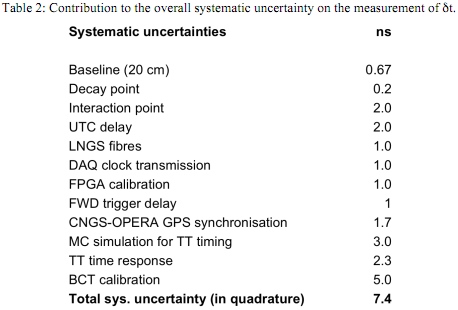
Well, fair enough, only 7.4 nanoseconds worth of error on that, assuming that there are no unidentified sources of error and that the identified sources of error are unconnected to one another. (I.e., that you can add them in quadrature, by taking the square root of the sum of the squares of all the individual errors.)
So they do a maximum likelihood analysis on their recorded neutrino data and see how much they actually have to delay their data by to get the best fit between the initial protons and the final neutrinos. If everything went as expected, they'd get something consistent with the above 988 ns, within the allowable errors. What do they actually get?
A craptacular 1048.5 nanoseconds, which doesn't match up! Of course, the big question is why? Why don't our observed and predicted delays match up? Well, here are the (sane) options:
- There's something wrong with the 988 nanosecond prediction, like they mis-measured the distance from the source to the detector, failed to correctly account for one (or more) stage(s) of the delay, etc.
- This is a very, very unlikely statistical fluke, and that if they run the experiment for even longer, they'll find that 988 nanoseconds is a better fit than the heretofore measured 1048.5 nanoseconds.
- The neutrinos that you detect are biased in some way; in other words, the neutrinos that you detect aren't supposed to have the same distribution as the protons you started with.
- Or, there's new physics afoot.
Now, the OPERA team basically wrote this paper saying that the first option is what they suspect, but they don't know where their mistake is.
We can look at the second option ourselves and see how good a fit a delay of 988 nanoseconds actually is compared to the data. The way they got their 1048.5 nanosecond delay as the best fit was to fit the edges of the distributions to one another. Here's the data from those portions.
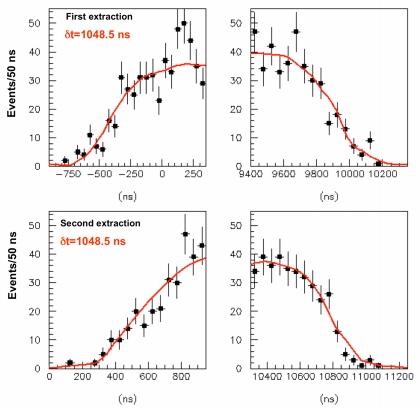
And while this is a very good fit, I've gone and generated an image of the graph in the upper-left-hand corner with, instead of the data points having a 1048.5 ns delay, only having a 988 ns delay. Let's compare.
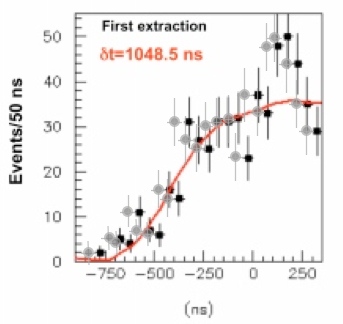
As you can tell just by eyeballing it, this fit isn't significantly worse. It is slightly worse, but despite the claimed six-sigma statistical significance, you'd be hard-pressed to find someone who claims that this fit is inconsistent with their data. Their analysis simply says that it isn't the most likely fit based on the data.
But there's also the third option, that I haven't seen anyone else talk about yet. And this is important, because I've seen people present at conferences claiming to have achieved superluminal velocities, and they are fooling themselves. Let me explain. (The next four images are mine.)
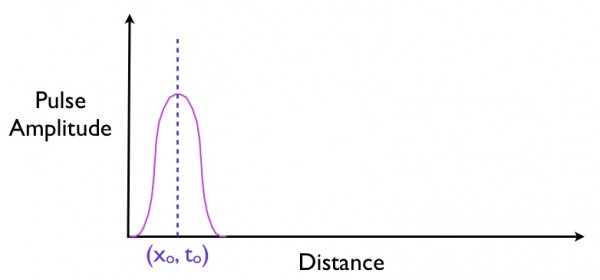
Imagine you start off with a pulse of "stuff" at an initial time, to -- whether it's light, neutrinos, electrons, whatever -- moving at just about the speed of light in vacuum. The pulse, of course, has a finite amplitude, lasts for a certain length of time and exists at a certain location.
What do you expect to happen at some later time, tf?
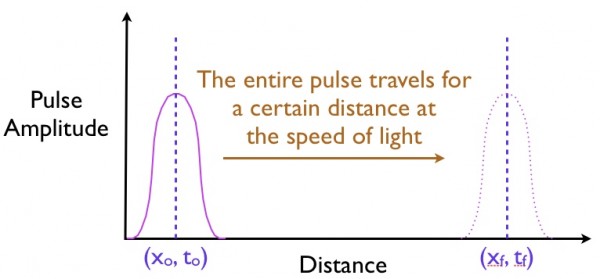
You expect that the pulse will move a distance in that time that corresponds to it traveling at the speed of light for that time.
But what if you can't observe the entire pulse? What if you can only observe some part of the pulse? This might happen, possibly, because it's hard to detect, because something happens to filter the pulse, etc. Quite often, you'll see results like this.
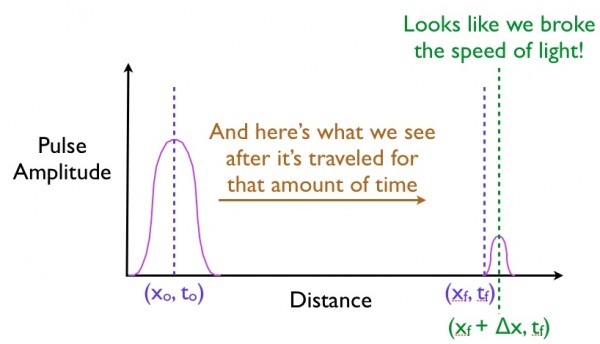
If all you did was measure the location of the final pulse (or what's left of it), you could easily conclude that you went faster than the speed of light! After all, the pulse appears to travel a distance (from xo to xf + ∆x) that's greater than the distance it would have traveled had it moved at the speed of light (from xo to xf).
But you're misinterpreting what you're seeing. You preferentially cut off the rear portion of the pulse!
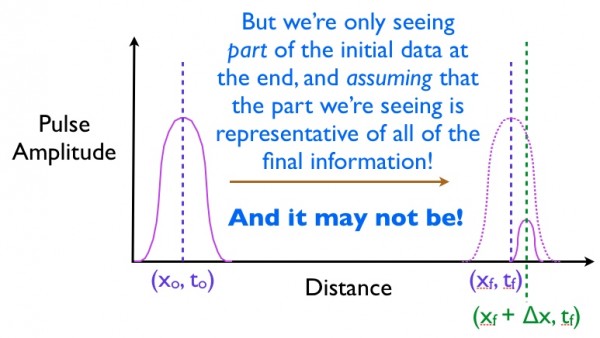
And really, nothing moved faster than the speed of light. Each particle -- each quantum -- moved at (or slightly below) the speed of light, but you only measured some of the particles at the end, and so your results got skewed!
This happens very frequently when people talk about group velocity and phase velocity in waves, which perhaps this animation below illustrates clearly.
The speculations about how the theory might be wrong are, of course, already abundant. Sascha points out how extra dimensions could be the new physics that accounts for this mystery, Bob McElrath and others have pointed out to me (privately) that the Earth could have an index of refraction less than one for neutrinos, and of course neutrinos could be some highly modified type of tachyon, among other explanations.
But before we can take any of these suggestions seriously on physical grounds, we've got to consider the possibility that there are errors either in the experiment, the analysis, or the selection of neutrinos!
Because you must not fool yourself, and you are the easiest person to fool.




Did you email this to them? Or plan to?
Great article.
Please excuse my ignorance on the subject, but how can refraction increase the apparent speed of something? Wouldn't that cause a curve in the path and make the distance from A to B actually longer, and therefore the speed slower?
Daniel R,
I wasn't planning on it, because I'm assuming that they're all working on trying to figure out whether there are any "option 1" mistakes that they made. I also assume that, as full-time experimentalists, they know much more than I do about all of these possibilities.
But if you wanted to send it to them, I certainly wouldn't object. :-)
And then there's SN1987A...
My bets also on option 1
Ethan, since the distances involved are measured via GPS, which in turn depends heavily on the value of C, what happens if this just shows that the assumed value of C was off by a minute fraction? If the true speed of light is a tiny bit faster than C, the triangle described by the GPS locations and the satellite gets a tiny bit smaller, making the neutrinos arrive earlier.
How is C measured independently if it's involved in the definition we use for length in the first place?
@Ethan #3: OK, I sent an email to Antonio Ereditato at Cern, giving him the Web address of this page. Hope he has time to look at it and make remarks in the comments! (I asked him.)
Regarding SN1987A: According to Wikipedia, the observatory that detected the majority of the neutrino emissions (Kamiokande II) became operational earlier that year. The other two, IrvineâMichiganâBrookhaven, and Baksan Neutrino Observatory, became operational in 1977 and 1982, respectively. According to http://heritage.stsci.edu/1999/04/sn1987anino.html: of the neutrinos from the supernova, the split was 12, 8, and 5 respectively.
So we can definitely say that some of the supernova's neutrinos were detected at the expected time. But has anyone gone back the ~3 years the OPERA experiment would predict we would find neutrinos and seen if there was a spike?
Could it be that the earlier neutrinos kind of "saturate" the detector for a while, which would prevent neutrinos arriving later to be detected and thus make us believe that the whole packet travelled at a higher speed than it actually did?
Interesting point. CERN should know this.
If CERN's claim is true, the experiment could be modified to reduce the pulse interval to less than 60ns and increase the intensity of particles within the beam and perform more tests with it.
Any candidates for the mechanism of bias in option 3?
Perhaps the target is getting saturated during the pulse, so that protons on the early end of the pulse produce neutrinos more often than later protons do.
Ethan, yes yes; there are many possible errors.
(by the way the CERN paper is relatively readable).
Ethan, I assume your explanation amounts to an experimental error in the end time accuracy (not the end time precision). And not an uncertainty principle error. OK, makes sense as a candidate explanation.
It's tempting to second or wildly guess; but I'm waiting for an accepted explanation or an accepted mystery. Hoping for a mystery (e.g. a Michelson-Morley for this century).
Could you explain how You preferentially cut off the rear portion of the pulse isn't the same as option 3?
Bruce E,
It is the same as option 3; I was attempting to explain how option 3 works.
Sorry if that wasn't clear.
Would it be possible that neutrinos created late during the burst have a higher chance of getting recaptured by the particles remaining from earlier collisions ?
The article here is great, I have a better understanding of how the experiment was conducted. Have to say very interesting experiment.
Is it possible they are not detecting the same neutrino that started but a different one!
The pulse events are out of 150ns
Discrepency is 60ns within 150ns
1/2
What was the original goal of this experiment?
Interesting post here:
"The 919 neutrinos above in the âend regionsâ determine most of the statistical power of the experiment; the other 15,192 neutrinos only reduce the statistical error by a further 1.8 ns.....Roughly speaking, what occurs in the first and last microsecond of each burst is overwhelmingly of greatest importance; what happens in the ten microseconds in between is less critical."
And:
"The Palmer analysis puts beyond all doubt the statistical significance of the OPERA result. It is extremely elegant, and yields a statistically sound approximation that is simple enough that even high school students can check the calculations. It also allows a rough quantitative estimate of the relative importance of the âend regionsâ and the âplateau regionâ in analysing the systematic uncertainties in the OPERA experiment."
http://johncostella.webs.com/neutrino-blunder.pdf
I have nothing useful to add to this fascinating discussion. So instead I will add something useless: http://i.imgur.com/Bnbuh.gif
Could electron neutrinos have been created at the beginning of the pulse and oscillated during the time of flight, changing to muon neutrinos while muon neutrinos created at the end of the pulse changed into another neutrino flavor, thus shifting the apparent output pulse forward by about 7 meters.
What source of power are used to accelerate protons in CERN experiment? May be it can generate more neutrinos when under increased demand of power to accelerate protons. And so done it earlier.
Well, this post is interesting, but what is not less interesting is the citation of Feynman. You see, you (Ethan) are speaking about the need of one to be careful from fool oneself, and I look at you, theoretical physicists, and even if it is not so politically correct to say the following,
it seems that you are fooling yourself in many ways and in a much deeper way.
Just recall all the claims about worm holes, the "other" universes which are just waiting for us inside these holes or in the other side of
these holes (or inside black holes), stories about 10 or 26 dimensions which are hiding somewhere, and so on. It is not better than science fiction or "One Thousand and One Nights". You don't have any single experimental evidence to these worm holes like stories, but you speak (well, at least some of you like
1. You
http://scienceblogs.com/startswithabang/2010/04/do_we_live_inside_a_wor…
2. Stephen Hawking
http://www.dailymail.co.uk/home/moslive/article-1269288/STEPHEN-HAWKING…
3. Kip Thorne
http://prl.aps.org/abstract/PRL/v61/i13/p1446_1
Michio Kaku
http://mkaku.org/home/?page_id=423
)
as it is completely true from the theoretical point of view but perhaps, currently, somewhat not practical because of technological limitations.
So to be honest with you, it is much easier for me to believe in particles/bodies moving faster than a certain arbitrary constant c (even if eventually it will be shown that the OPERA experiment was wrong in one way or another) than to believe in the stories that respectable
physicists tell themselves and the public.
Daniel (no relation to Daniel R from #1, #3)
Ethan - Very good analytical summary that even this pedestrian could almost follow.
While the distance between the proton extraction and final neutrino detection sites has been precisely estimated (presumedly that of a straight line rather than a geodetic arc?), there is no way to determine the actual path taken or distance traversed by detected neutrinos, correct?
While the neutrinos are described as a 'beam' they would actually disperse as they propagate, correct? Doesn't this explain the exceedingly small detection sample?
Wouldn't the non-zero mass neutrinos interact with the Earth's gravitation during their 730km journey?
Wouldn't the non-zero mass neutrinos produce some relativistic local contraction of internal spacetime within the Earth while travelling at velocities near c?
Would any or all of these potential factors significantly invalidate the baseline distance approximations?
I appreciate any consideration that might be given.
Here is another example showing how theoretical physicists
act in a way which is somewhat related to what Feynman said:
When listening to theoretical physicists, or, in fact, to astrophysicists, one has many opportunities to hear about relativity theory and how it is deeply related to astrophysics. One then hears that massive bodies distort the time flow around them, that the time in a one moving body is different from the time in another moving body, that time and space are intimately related and there are no separated space and time but rather a combined spacetime, and so on. One also hears about all the massive bodies in the universe, about the so many galaxies which move so fast with respect to each other and so on.
But then one hears the story about that thing that started with a bang, and how this glory event happened, and suddenly, it seems that the speakers completely forget all the theories they have just mentioned about spacetime, about different time flows, and so on: there is a space, which is separated from time, and in this space there is one universal inertial frame, and that glory event happened in this space in a certain roughly known point in time, and perhaps in the (universal) future there will be another glory event which will end everything with a bang.
There is a blind spot in this experiment which I don't see people mentioned: c is the speed of light in VACUUM. In this experiment, the neutrinos are traveling through SOLID MATTER, ie. Swiss and Italian earth. If the measurements are correct, it might mean that there is some anomaly when particles, neutrinos or otherwise, travel through the core of other particles (protons, neutrons etc).
If the source and target distributions do not match (option 3), would an ML estimator provide six-sigma certainty? Isn't the residual error of the estimator going to be higher? Option 1 is possible, but I guess it would by now be the reviewer's responsibility to specifically point out what likely sources of systemic error exist. Few concrete objections seem to have surfaced.
What was the original goal of this experiment?
Have you heard the one about the fellow looking for his keys under the lamppost?
Hi Ethan, thanks for mentioning my article. Please note that the extra dimensions are only a didactic tool - it was not the main point. The gist is that superluminal velocity does not necessarily violate relativity or causality; this holds independent of there being extra dimensions. I will today post another article that explains this further.
Of course, just for the record, we all assume this to be a systematic error as I clearly pointed out here:
http://www.science20.com/alpha_meme/one_way_light_velocity_toward_gran_…
Dario Autiero's talk at CERN is available on a webcast, here
http://cdsweb.cern.ch/record/1384486
There's about an hour's talk and an hour of questions.
The two main issues that you raise come up together in the questions.
Start at slide 79,80 - these show what you've attempted above,
the fit of the leading and trailing edges with no effect compared to
the max likelihood estimate 60ns. Stay with it until slide 83, they
come back to it.
Questioners share your skepticism about the fit. The authors justify
by saying that all the squiggles in the top of the distribution
contribute to the max likelihood calculation, but this is challenged -
given the roughly square shape, probably only the data at the edges
contribute to precision, so chi-squared may be worse than reported.
In other words, only a few hundred of the 16,000 data points
really contribute to the 60ns estimate.
For the second extraction, the fit of the leading edge data looks much
worse than the trailing edge. Since this raises the issue of whether
the data fit the predicted pdf's (derived from the protons) at all, it
leads to questions about detection bias, i.e. your issue 3 above, but
these questions don't really get far.
What about Pilot Waves as in de BroglieâBohm theory, travelling ahead of the actual Neutrinos?
The way you explained option 3 would only be plausible, if the "width" of the proton PDF would be larger than the time interval where the events are measured, which is clearly not the case. they spread over roghly 10 micro secs in the first extraction and 12 micro seconds for the second extraction.
Rick DeLano: "The 919 neutrinos above in the âend regionsâ determine most of the statistical power of the experiment; the other 15,192 neutrinos only reduce the statistical error by a further 1.8 ns.....Roughly speaking, what occurs in the first and last microsecond of each burst is overwhelmingly of greatest importance; what happens in the ten microseconds in between is less critical."
That was my main concern with their fitting as well. Decreasing the length of the pulse should give better statistics; whether this raises other issues I'm simply not qualified to tell.
Here is the article explaining that the assumption of extra dimensions is not necessary for particles to go faster than light without violating relativity or causality:
http://www.science20.com/alpha_meme/faster_light_neutrinos_do_not_time_…
It will be interesting to see if 160 world-class physicists have managed to fool themselves. Had this been 'three guys in a lab', I would expect that they have done so....but 160 really skeptical guys and gals desperate not to embarrass themselves? Time will tell.... (that is, if they're wrong, time will tell. If they are right, may time won't tell?)
How does the uncertainty principle come into play here?
If the rear end of the pulse was cut off, would they be able to detect that by seeing that the two pulses don't overlap without rescaling the time axes?
You need to fit the leading edge AND trailing edge of the distributions SIMULTANEOUSLY. If you do that in the example above does the trailing edge also give a good "eyeball" fit?
I'm pretty ignorant of this subject, but I was curious: how much would the gravity of the earth and other object, the sun, moon, etc, affect these experiments?
I'm really surprised at the method they used of binning their neutrino data and doing a curve-shape fit.
With the countably low statistics available on neutrinos, it puzzles me as to why this group of experimental particle physicists eschewed the more conventional technique of constructing a cumulative distribution function for the leading and trailing edges and using the Kolmogorov-Smirnov test to determine the best fit. It seems to me that you'd want to avoid binning your data with low (50 ns) resolution if at all possible.
But, even if it isn't obvious to me, I'm sure they have their reasons. Anyone know?
If some neutrinos are selectively lost at the detector in a biased way, an averaging method might give systematically incorrect results. If all later neutrinos get dropped, for example, averaging would show faster-than-light neutrinos.
Maximum likelihood estimators are more accurate. If all neutrinos do move at the same speed, and assuming no noise in the measurements, it won't matter which neutrinos get dropped. The estimator will return the correct speed with a perfect fit. In reality, there will be noise and hence the fit is imperfect. But a bias in how neutrinos are dropped won't skew the results easily. One could, of course, come up with artificial data sets which could fool the math, but those are unlikely from natural sources of error. The most parsimonious explanation, if one assumes there is no measurement error and the physics model is accurate, is that the reported speed is correct.
Option 3 doesn't seem a tenable objection. Option 1, of course, stands, but gets weaker as an objection every day the result continues to stand scrutiny.
Ethan,
Where does the paper talk of the 50ns resolution for binning to calculate the PDF/CDF? That is a real question, not a rhetorical one. I am not a physicist; it is hard to read to get just the math part from the paper.
Ethan, I don't know their exact protocols, but making certain "reasonable" assumptions about the distribution (I know!), it shouldn't matter how many bins you use to the limits of resolution as long as you have many more pieces of data than there are bins.
I'm not saying your suggested test isn't a good one, or not a better measure than the one used, just their procedure won't give a figure different from the true one by what looks to be a rather small margin given the number of data points. Of course, the difference - 60 ns - is on the order of the bin size, 50 ns, so your idea is certainly worth checking out! Given your recent big career decision, it strikes me that applying this test yourself might be something well worth doing. We certainly hear enough complaining about how science types don't know their stats.
It seems quite unlikely that the neutrinos would have traveled at the same speed. Their propagation characteristics are not as simple as those of photons.
As I understand, evidence indicates that neutrinos oscillate between their three flavors at rates that vary in certain conditions. Each flavor is considered to have differing but tiny amounts of mass. Particle propagation velocity is inversely related to its mass. A MSW effect (see below), also known as the âmatter effectâ, can modify the oscillation characteristics of neutrinos in matter.
I have found some seemingly related discussions in wikipedia.
http://en.wikipedia.org/wiki/Neutrino_oscillation
http://en.wikipedia.org/wiki/Neutrino_oscillation#Beam_neutrino_oscilla…
http://press.web.cern.ch/press/PressReleases/Releases2010/PR08.10E.html
âOn 31 May 2010, the INFN and CERN announced[2] having observed a tau particle in a muon neutrino beam in the OPERA detector located at Gran Sasso, 730 km away from the neutrino source in Geneva.â
http://en.wikipedia.org/wiki/Neutrino_oscillation#Propagation_and_inter…
âEigenstates with different masses propagate at different speeds. The heavier ones lag behind while the lighter ones pull ahead. Since the mass eigenstates are combinations of flavor eigenstates, this difference in speed causes interference between the corresponding flavor components of each mass eigenstate. Constructive interference causes it to be possible to observe a neutrino created with a given flavor to change its flavor during its propagation.â
http://en.wikipedia.org/wiki/Mikheyev%E2%80%93Smirnov%E2%80%93Wolfenste…
âThe presence of electrons in matter changes the energy levels of the propagation eigenstates of neutrinos due to charged current coherent forward scattering of the electron neutrinos (i.e., weak interactions). The coherent forward scattering is analogous to the electromagnetic process leading to the refractive index of light in a medium. This means that neutrinos in matter have a different effective mass than neutrinos in vacuum, and since neutrino oscillations depend upon the squared mass difference of the neutrinos, neutrino oscillations may be different in matter than they are in vacuum.â
âThe MSW effect can also modify neutrino oscillations in the Earth, and future search for new oscillations and/or leptonic CP violation may make use of this property.â
The KS-test figures out how close two distributions are. The KS-test would work if one assumes the detected neutrinos are a random sample of those originally generated, an assumption which suffers from the problems you mention as option 2.
In this case, we are interested in identifying the protons in the extraction distribution which gave rise to the detected neutrinos. The ML estimator seems the right model when we are unsure if there is systematic bias in how the neutrinos end up getting detected.
"Faster-Than-Light Neutrinos Definitely Not a Statistical Blunder, Says Scientist":
http://www.pcmag.com/article2/0,2817,2393587,00.asp#fbid=lmjcGPhhw5s
The physicist in question is John Costella. He firstly said that their method was wrong, but changed his mind after having received a response from Cern:
http://johncostella.wordpress.com/2011/09/27/do-operas-tachyonic-neutri…
http://t.co/0qVZSuqf
I just posted a comment, but the spam filter seems to have refused it. Here the main link of this message, hope it works:
http://www.pcmag.com/article2/0,2817,2393587,00.asp#fbid=lmjcGPhhw5s
A K (ajoy and ScentofViolets,
Unfortunately, OPERA has not released their raw data to the general public, so even if I were inclined to do at KS test myself, I do not have access to the necessary data to do so.
James Dwyer,
The maximum mass of any light neutrino is restricted to be less than 0.24 eV/c^2, while the energies of each neutrino is in the GeV range. Over a 730 km baseline, the difference in arrival time between the most and least massive neutrino is much less than 1 ns, so this cannot account for the difference.
For those of you who do not wish to get caught in the spam filter, be advised that any comment with more than one link in it will certainly trip the filter. And if you've offended it before, it's possible that even a single link will do so. I'm always happy to release it when I know about it, but that sometimes takes up to 24 hours.
A K - I think the ~ 50ns scintillator response time is briefly described (a schematic would help) in the next to last paragraph on pg13 in the OPERA report.
I can't really follow the discussion either, but I think that infers at least that neutrinos interacting with the activated scintillator strip during that 50ns would not be detected. In the worst case, no neutrinos would be detected by the entire Target Tracker device once a neutrino was detected by any scintillator strip, but that surely can't be the case - thus the many scintillator strips.
However, so few emitted neutrinos are actually detected it is very important to understand on what basis they are being selected!
Of course neutrinos interaction with any material detector is simply highly unlikely.
Is dispersal of the neutrino 'beam' making detection of many neutrinos by the small detectors impossible? In this case neutrinos detection may be selected by beam/detector geometric alignment.
Are the detectors busy processing initial (faster, 'lighter' neutrino flavors produced by oscillation) detections while many subsequent emissions (perhaps slower, 'heavier' neutrino flavors) are not detected?
Other factors may be contributing to the selection criteria for detected neutrinos. Only if the neutrinos reaching the detectors still represent a random sample of the total emission population and they are being randomly selected for detection will the statistically derived Time of Flight be valid.
It's not just the tail of the proton distribution gotten cutoff that can lead to bias, if the front of the distribution did not generate neutrinos that reach the detector, the departure time would also have been biased.
May be detectable neutrinos won't be generated until a proton hits the product of another collision. Or may be multiple collisions in a sequence is necessary to generate detectable neutrinos. If this is the case, this would result in bias favoring the end of the departure distribution.
Ethan - While the effect of oscillation between neutrino masses cannot account for the 60ns, if only the 'fastest' neutrinos are detected, then the detectors are busy, results would be skewed, correct?
James,
If you calculate the event rate, you will find that they only detect about one neutrino per hour or two of operation; it is extremely unlikely (like, worse than one-in-a-million odds) to have two neutrinos from the same burst interact with the detector.
Ethan - Wow, I had missed that completely. Even now, scanning the report I don't find any mention of that - I guess that's something only a qualified physicist would know... Thanks!
Thanks for the additional info and explanations Ethan.
But I'll still go with door #1, Ethan (specifically an error of distance).
Hopefully "when the door opens" and the facts revealed, somebody will send me some six packs (I prefer dos equis XX), but nobody has bet me yet :( Doesn't anyone else want to make a specific prediction and win (or lose) some beer from (or to) me by making a bet with me? :)
Fun fact I just thought to mention:
And all those protons together had a mass of about 1 milligram. Sounds like a lot, but it's so little!
Fascinating comments and speculation! A couple background questions please: 1) How does the density of the neutrino beam that starts out from the CERN accelerator compare to other streams in our neighborhood (via distant novae, supernovae, etc.) and 2) is there any significant difference in the weakly-interacting properties of neutrinos to other mater compared to other neutrinos (or types)?
Oops, that was supposed to be one-sixth of a milligram. Not sure if the blog eats fractions, or I just typoed over the part after '1'.
Some refered above to an idea I had - what is the difference from a "straight" line in travel through the earth because of gravitational warping of the path? Would that not cause a different expected light or neutrino travel time? Seems a possible source of error - after all, they are not comparing the neutrino travel time with a parallel beam of photons!
@Gary Sjogren,
A warped path of travel is a bent path which would be a longer path. If there was an error of distance involved it would be due to distance under estimation/ "measurement". To calculate for a longer distance caused by a warped path (longer path), would result in a bigger discrepancy :(
I think I found what might be the problem; the systematic sampling bias that Ethan postulates is the problem. I get this from the thesis of Giulia Brunetti from the OPERA official site. Chapter 4.3, page 65 or so.
The scintillation fiber has a limited angle of acceptance. Photons can be generated anywhere in the plastic and can move in any direction. Those that move in certain angles are collected and transmitted by the wavelength lowering fiber. Those that move in different angles are lost. The time it takes for a photon to reach the PMT depends on the angle that it moves at. Those that move at lower angles take a longer path length to travel to the PMT and so have a longer delay. These photons are also more likely to be lost due to both absorption and also due to the angle of total internal reflection.
The delay in the fiber is calculated from laboratory measurements of the mean delay measured in a fiber. There is dispersion in the delay, the delay gets longer the longer the light is in the fiber. The light gets more attenuated the longer the delay.
What I think they are doing is curve fitting the output pulse to a model of what light inputs give that light output. That model uses both the light intensity recorded and also the timing of when the light was recorded, the dispersion of the transit time and also the mean delay time in the fiber as measured in the laboratory.
However, the system is set up to only record events where there are at least 10 triggers, that is where at least 10 PMTs have triggered, and then the fastest trigger (as calculated by the model) is taken as arrival time of that neutrino.
By only taking events where there are at least 10 triggers, the sampling is biased to only take events that have high light acceptance angles (and so are high magnitude events) and also events that had a low delay time (because they are high magnitude events). Using the mean delay as a fitting parameter when the distribution of events is biased by selection is (I think) not appropriate.
I think what this is doing is truncating the sampling of events that occurred later in the neutrino pulse (because their delays are too long), and events that occurred in certain parts of the apparatus (where they give long delays and attenuated signals).
There are two skewing events here. The skewing at the front end of the neutrino pulse only detects high magnitude (>10 trigger) events which are skewed to register as âfasterâ. The skewing at the back end is the rejection of the âslowâ events that occur in the long time delay regions of the detector because they are low magnitude.
As Ethan points out, you don't need to move very many points by very much to change the âoptimumâ fit. If a few hundred or a few thousand data points were rejected because only 7, or 8, or 9 PMTs were triggered, and those happened to be âlateâ events, that could skew the whole distribution. Unfortunately the thesis says that only events with 10 triggers were recorded, so the 7, 8, 9 triggers might be lost. Looking at the relative timing of events vs the number of PMT triggers would be an important parameter. If there is bias, then it should show up in a skewed distribution.
If these neutrinos are moving faster than light, then their mass/energy which started out as subluminal protons somehow got accelerated to FTL so that the mass/energy that caused the interactions that was observed could arrive at the detector before light could. If real mass/energy can't be created or destroyed, then imaginary mass/energy or negative mass/energy can't be created or destroyed either. Where are the exotic particles with imaginary or negative mass/energy? None of them showed up in the detector and they looked pretty hard at what was detected. If they found some wild and exotic thing they would have reported it.
Did they work together with any statisticians?
Ethan: I'd assumed that the 50ns binning was just for the plot. They don't mention what binning they used for the fit, could well be unbinned.
I'm leaning towards option 3, mainly because option 1 would be really boring. You just need the leading edge to be more likely to result in a neutrino hit than average, and the trailing edge to be less likely, and there you go. narrower/wider angular distribution (respectively) would do it, for one. The experiment as a whole has no particular incentive to get the edges right in Monte Carlo (makes damn all difference for mixing measurements). Its pretty unlucky to get a bias like that that preserves the basic shape, but not 6 sigma unlucky, I'd say.
When I saw what you are showing in your illustration of how they measured stuff something stuck me there is a possibly another explaination
Look at L. J. Wang, A. Kuzmich & A. Dogariu work with gain-assisted superluminal light propagation. (http://www.nature.com/nature/journal/v406/n6793/abs/406277a0.html)
Initially it was met with howls from skeptics but now is routinely accepted and explained
(http://www.eleceng.adelaide.edu.au/thz/documents/longhi_2003_stq.pdf)
(http://www.phy.duke.edu/research/photon/qelectron/pubs/SFLProgressInOpt…)
What to me is interesting is look carefully at the effect and what you see.
I had not seen an explaination of the results as you had shown and what is being seen could be as simple as matter (IE earth) has a slight gain assist to nuetrinos.
That in itself of coarse would be very very interesting but leaves the value of C intact as it does with authors above work.
Your qualitative discussion of of biased selection can induce an apparent shift of the mean was quite nice (and I've already used it a couple of times to explain things to non-physicists; thank you!).
There's a one-page preprint out on arXiv which works through exactly this possibility quantitatively, arXiv:1109.5727 (I hope that doesn't trip the filters :-).
Alicki solves a pseudo-Dirac equation for the case of a damped distribution (which essentially integrates over all of the various effects which reduce the 1020-proton spills to 16k neutrino events). He shows that the damping leads to a very simple apparent shift in position, just as in your diagram, and he also suggests that the observed time discrepancy is consistent (within 3 orders of magnitude out of 16, cough) with the neutrino/proton efficiency.
daedalus2u - Very interesting! The document you reference was difficult for me to find at: http://operaweb.lngs.infn.it:2080/Opera/ptb/theses/theses/Brunetti-Giul…
It is a very clearly written 128 page discussion of neutrinos and the experimental equipment. It is by far the best source of information about the equipment and its operation that I've seen.
Having only briefly scanned this document I find that the physical alignment of the CNGS beam and the OPERA detectors is considered critical and has been carefully studied. Most of the monitoring and adjustment seems to be performed at the CNGS site. Any beam dispersion or curvature effects that might occur during transit, affecting detection seem to at least be within simulation tolerances. This is just a sample of information that I've not found elsewhere.
I have yet to find a discussion of the 10 trigger event threshold, but if the angle of beam alignment is altered by external conditions as the beam propagates, that might affect the triggering of events as you say. I'll have to defer any further investigations as my meager abilities are waning for the night.
Good find,daedalus2u!
Sorry if this has already been covered. What I cant understand is why they seemingly averaged all the proton measurements together, then compared that to the neutrino counts. Wouldn't it make more sense to compare each firing of protons to its accompanying neutrino detection, then doing averaging? Heck, shouldn't they have only averaged the proton results from the packets that created detected neutrinos? I assume I missed something. What is it that I'm not understanding, did I misread the measurement/analysis they did?
I may be obstinate, but if oscillations of muon neutrinos into tau neutrinos with greater mass (discussed in the thesis referenced in my preceding comment) the pulse approaching the vicinity of the detector might consist of a head containing muon neutrinos and a small tail containing slower, heavier tau neutrinos. Moreover, the geometric alignment of the heavier tail to the detector might have been skewed by gravitation. In this speculative case perhaps only the properly aligned muon neutrinos in the head of the pulse would meet the trigger detection threshold described by daedalus2u, producing the biased detection distribution and the invalid timing results described by Ethan.
Perhaps this finding is not so mysterious, perhaps it primarily gives us a slightly more accurate measurement of the cosmic speed limit.
Light is slowed down by the material it travels through, and the "empty space" that we measure the speed of light traveling through, is not really empty.
Neutrinos are notoriously slippery, it would not be surprising to learn that neutrinos are slowed down less than light when traveling through "empty space" (the quantum foam of virtual particles popping in and out of existence, and likely other unknown properties of the mysterious ether).
About SN1987A neutrinos and photons.
We can't be sure that the emission of neutrinos and photons from the supernova happened at the same time. We weren't there when these were emitted from the Star. So we should be extremely careful when we try to interpret the data once these are detected on Earth. It would take much more data from many other galactic sources to test if the data from SN1987a is typical or not. On the other hand the OPERA experiment we have better knowledge of when and how these neutrinos were emitted, the distance travelled, and also the detectors were set specifically for that neutrino source.
Anyway, a great day one way or the other for experimental physics!
James, that was on page 52.
I think I interpreted that correctly.
daedalus2u - Thanks - finally, at the end of section 3.3 'The OPERA Detector'!
The final detection criteria statement is:
"Finally, a coincidence of 2 consecutive TT planes (XZ and YZ coincidence), or of 3 RPC planes is required. Then, the event is retained if it has at least 10 hits."
I interpret the statement to indicate that the track of the neutrino interaction is spread across multiple detectors in at least two of three dimensions, with a total of 10 components registering hits (or possible just 10 hits total).
At any rate, it'll take quite a bit more reading to gain a reasonable understanding but I don't see any problem with your prior assessment.
The only question seems to be: what detection bias would selectively exclude detection of the emission pulse tail - necessary to produce the timing error described by Ethan? As I understand the sensitivity of the detectors to the geometric (geodesy) alignment with the neutrino beam, I suspect that it is the segregation of heavier/slower tau neutrino oscillations to the tail of the mostly lighter/faster muon neutrino pulse that, because of gravitation, pulse dispersion or some other external influence alters the angular alignment of neutrinos in the pulse tail to the detectors, reducing their efficiency. This may only be speculation, but some mechanism is required to produce the selective exclusion of the pulse tail neutrinos from detection.
P.S. My confusion over finding text is the discrepancy between the page number labels and the actual page number reported by Adobe Reader. I suggest in the future we refer to the page number labels as 'page labeled n' or to the document section numbers and titles. The page labeled 52 is actually page 60 to Adobe Reader...
I think it is easier to appreciate how the detector skews the time of the detection compared to the actual arrival time at the detector.
If a neutrino happens to interact in a part of the detector where the amplitude of the signal it generates is small, that neutrino will register as having a slightly later arrival time that a neutrino that interacted at exactly the same time but which generated a signal of large amplitude.
If low amplitude signals have a later arrival time bias (and they do as I understand how the equipment works), and you truncate the signals you accept at some level, then you are biasing your sample for earlier arrival times.
This bias has nothing to do with actual arrival times, it is purely due to the magnitude of the signal.
In looking at the thesis more, there is another problem which looks to be even more severe relating to the instability of the timing at the two sites. This is discussed in figure 5.7 as a ~60 ns erratic discrepancy between the two simultaneous clocks. This appears to be the source of the ânoiseâ discussed in chapter 8.
In figure 8.4, 8.5 and 8.6 he mentions finding ânoiseâ of unknown origin on the proton beam waveform with 30/60 ns time components. This ânoiseâ is eliminated by âfilteringâ it out. This ânoiseâ is more apparent at the leading and tailing edges of the waveform.
I see no explanation and can think of no justification for filtering out this ânoiseâ. The proton beam waveform is recorded with a 1 ns resolution. Adding together many waveforms with a 1 ns resolution does not generate ânoiseâ of 30/60 ns. I suspect they needed to filter out this ânoiseâ to be able to use a most-likelihood analysis later.
What they are doing by âfilteringâ this ânoiseâ is adding 60 ns to some data points and subtracting 60 ns from others such that they get smooth curves.
I suspect that the noise on the timing signal is the ultimate source of the problem. That noise is on the same order as the deviation from light travel time that they found.
Without finding the source of that noise and eliminating it by doing new measurements, I am afraid their result is NFG, and they are fooling themselves. I feel bad for the guy who was doing his thesis when they found the erratic timing and couldn't fix it because the equipment wouldn't accept replacement and the runs had already been done.
But now they can acknowledge that filtering out the ânoiseâ was not a good idea and there is a triumph of post peer review that found this mistake.
"If your experiment needs statistics, you ought to have done a better experiment." - Ernest Rutherford
For all who want to research in detail all about the experiment, here can be found the sources. Unfortunatelly they haven't made the data gathered available, but at these links are 47 thesis papers from scientists at OPERA and 36 publications. Each document is about the specific part of OPERA, from detector working, plate and film properties, manufacturing, measurments, analysis, statisics.. etc.. enjoy. If there's a human error of the experiment, it's probably inside of these.
http://operaweb.lngs.infn.it:2080/Opera/phpmyedit/theses-pub.php
and
http://operaweb.lngs.infn.it:2080/Opera/phpmyedit/articles.php
daedalus2u - I had a more complete response when my browser hiccuped, so I'll be very brief. I generally understand your issue with detector delays, but can they produce the 60 nos discrepancy? I'm thinking not, but will continue reading as I can. Your' point out critical issues help tremendously - please keep it up!
The unexplained increasingly erratic timing 'oscillations' in 2009 & 2010 smell really bad. Makes one wonder about the data... I'll have to (slowly) do a lot more reading.
I do have to commend the author of this thesis for being so forthright about critical problems, but many of the necessary details seem to be unavailable. What's most telling is that all of this critical information seems to be missing from the official OPERA report...
Thanks again!
Cutting off one end of the distribution would definitely be a systematic problem, except they have measured both ends. That doesn't rule out a systematic error with the proton PDF etc. (On the other hand, the lack of widening of the PDF means that any simple "tachyonic neutrino" explanation has problems: http://t.co/PpSokwji )
On the off chance that the OPERA result is correct, the simplest explanation to me is that the neutrinos got across the 18-metre hadron stop essentially instantaneously (i.e. as distinct to the 60 ns it should have taken them at the speed of light). This might sound crazy, but it's within the realm of the Standard Model (with a bit of condensed matter uncertainty) without the need for too many exotic extensions: http://t.co/lOzF0IYF
A K wrote:
I'm restating here some things I wrote up elsewhere, so also look at this and this.
If I had to guess where there might be bias, it would not be at the detector, but earlier in the overall process. I could imagine bias in pion/kaon production at the graphite target, for example - maybe more pions/kaons at the beginning of the 10 ms pulse, before the target's temperature shoots up because of the pulse?
If the creation of neutrinos (per proton) at the target were biased towards the beginning of the pulse, it would bias the results towards superluminality.
There is a big assumption here. The MLE works only to find the best fit among the possibilities being considered. It seems the researchers assumed that the neutrinos were a random sample from a neutrino arrival distribution that had a shape identical (except for a constant scale factor) to the summed proton waveform. In other words, they assumed no beginning-to-end-of-pulse bias across the several intermediate processes between protons emitted and neutrinos detected. The MLE used a one-parameter family of possible fits, the parameter being delay.
If the actual neutrino arrival distribution was not considered as a possible fit, then while the fit found is the best of those considered, the interpretation that the offset of the fit - the systematic delays = time-of-flight if not valid. Perhaps the actual neutrino arrival distribution (which was probably randomly sampled) was "tilted" from the summed proton waveform shape - say 3% higher at the beginning of the pulse and 3% lower at the end. The best fit time delay for this tilted shape might be greater than 1048 ns by enough to matter.
Again, no, not if the correct shape to fit against was not considered. For example suppose you run a fantastically careful experiment to measure something. Then you fit a linear function to the data and find a best fit slope is 1.2 plus/minus 0.2. If the data is a sample from a subtly curved process, the interpretation of 1.2 as meaning something specific about your experiment is not going to be right. (The chi-squared hints at the goodness of the model, and hopefully the authors checked the residuals for heteroscedasticity, but they don't mention it - and I see hints there is some in the binned data.)
I only agree that Option 3 is not tenable if I can be convinced that the actual neutron arrivals (a tiny fraction of which were detected in an unbiased way, I assume) were distributed over time exactly in the same way the protons were generated hundreds of miles and several interactions away.
The more I think of it, I think the filtering out of the 30/60 ns "noise" is the source of the error.
You can't just apply "filtering" to your data when you don't like the way it looks. The justification was that then needed timing accurate to 1 ns resolution, so they filtered out the 60 ns noise? That makes no sense at all.
If the precision of the measurments doesn't support a 60 ns analysis, applying "filtering" doesn't improve the resolution.
Why don't they analyze the data without filtering it? That would be the usual practice. There is no need to filter the data, it is purely aesthetic. Trying to make things look "pretty", or the way you think they should look is one of the easiest ways to fool yourself. That was one of Feynman's classic examples, people looked for errors until they got the "right" answer, the answer that was close to what earlier researchers had found.
daedalus2u - The Giulia Brunetti thesis, "Neutrino velocity measurement with the OPERA experiment in the CNGS beam", http://operaweb.lngs.infn.it:2080/Opera/ptb/theses/theses/Brunetti-Giul… seems to report in section 8.1 on page label 124 that the cause of the "strange âoscillatingâ behaviour" were not understood, but were discarded. On page label 125 it was explained that an even larger "internal oscillating structure" appeared. Its cause was 'explained' as: "not caused by the proton beam but that was due to a form of coherent noise synchronous with the beam".
IMO this describes characteristics of the inherently oscillating data but does not identify even any potential cause for the 'noise'. This unknown 'noise' is smoothed out and eliminated with no rationalization whatsoever. Of course, so many (~25% of all data) of the observations were affected by this significant data corruption.
Frankly, these charts of intermediate and final statistics show the elapsed run time (I presume) in ns on the x-axis, while the y-axis is labeled 'a.u.' I've not found any explanation of what this 'a.u' data actually represents. However, I particularly don't understand why the seemingly adjusted but otherwise identical representation of the same data should range from 0 to ~0.45 in the intermediate chart (Fig. 8.4) but range from 0 to 1.2 in the final chart (Fig. 8.6). The actual y-axis 'a.u.' data shown in Fig 8.4 is mostly around 0.4 whereas the final chart in Fig 8.6 is mostly around 1.0. I'd appreciate anyone helping me to understand what 'a.u' represents and why the data values have more than doubled.
My initial impression is that this data may be precisely measured but it is not dependable.
James, I think "a.u." means arbitrary units and is just a value showing a relative magnitude.
It isn't at all clear to me that the oscillations that are called "noise" actually are noise and not the proton beam actually changing.
I suspect that many of the authors of the report don't appreciate how nd why the data was "smoothed". I think if they did, it would have been mentioned.
I would really like to see an error propagation analysis that includes the potential error generated in the smoothing step. My guess is that source of error will dominate and is greater than the time differential necessary for FTL travel.
COMMENTS FOR THIS ENTRY CLOSED
-- James Ph. Kotsybar
When the general public hears about
A breakthrough in scientific research
They want to add their voices to the shout,
So as not to feel theyâre left in the lurch.
That they have opinions, there is no doubt.
Theyâll foist themselves into the dialogue,
When something sensationalâs put in print.
Though their comments reveal theyâre in a fog
Without having the slightest clue or hint,
It wonât prevent them posting to the blog.
Most often, all they can add is their moan:
âWhy canât science leave well-enough alone?â
daedalus2u - It appears you're correct re. arbitrary units. Personally I fail to see why the actual units were 'unknown'...
What is critically apparent in the data shown in Fig. 8.4 is that the a.u. generally increases in value as the extraction progresses until, at about 7,500-8,000 ns into the extraction some filtering is apparently applied.
At that time (~7,500 ns) the values of a.u. significantly diminish over a duration of about 1,000 ns.
At about 9,500 ns into the extractions the unknown source of oscillation begins.
The magnitude of these unknown oscillations progressively increases as the extraction progresses. This should be an important indicator of cause to those most familiar with the extraction process.
These characteristic apply to both the 2009 and 2010 tests.
That the oscillation begins at about the same time into the extractions and occurred in separate tests conducted a year apart should be highly indicative of the cause of what is most likely an error rather than any physical characteristic of the beam or of its neutrinos.
Since the a.u. value plotted represents a summary at a point in time for many extractions, the alternation of higher and lower values in time is particularly indicative of some effect occurring during that time in many but not most extraction runs. I would be surprised if simply segregating the extractions that had high values from those that low values would greatly help in identifying the conditions in which the higher and lower values occurred.
At face value, the data indicates that a.u. (arrival rate or whatever) wildly fluctuated every ns or so. Simply smoothing or smudging the value somewhere in between simply disguises the condition actually producing the data values.
As I said before, this oscillating condition occurs in two separate tests, about a year apart, in which the a.u. values generally increase as the extractions progress, then drop with filtering - then the wildly fluctuating data.
There are many conditions affecting the data collected that either are admittedly not at all understood or have been smoothed out or not even recognized. Why does a.u. initially increase, required filtering and then wildly fluctuate? None of the conditions producing these effects have been explained.
want to add their voices to the shout,
So as not to feel theyâre left in the lurch.
That they have opinions, there is no doubt.
Theyâll foist themselves into the dialogue,
When something sensationalâs put in print.
Though their comments reveal theyâre in a fog
Without having the slightest clue or hint,
It wonât prevent them posting
SN1987A, A Retrospective Analysis Regarding Neutrino Speed
In 1987 the physics community was surprised by a fortuitous supernova.(1) The light from the supernova reached Earth on February 23, 1987, and as it was the yearâs first supernova, it was designated SN1987A. The parent star was located in approximately 168,000 light-years away, in the Large Magellanic Cloud, which is the Milky Wayâs companion dwarf galaxy. It became visible to the naked eye in Earthâs southern hemisphere.
In this observation, a star core collapsed and released a lot of energy. Most of the excess energy is predicted in theory to be radiated away in a âcooling phaseâ massive burst of neutrinos/anti-neutrinos formed from pair-production (80-90% of the energy release) and these neutrinos would be of all 3 flavors, both neutrinos and anti-neutrinos, while some 10-20% of the energy is released as accretion phase neutrinos via reactions of electrons plus protons forming neutrons plus neutrinos, or positrons plus neutrons forming protons plus neutrinos (1 flavor, neutrino and anti-neutrino). The observations are also consistent with the models' estimates of a total neutrino count of 10^58 with a total energy of 10^46 joules.(2)
Approximately three hours before the visible light from SN 1987A reached the Earth, a burst of neutrinos was observed at those three separate neutrino observatories. This is due to neutrino emission (which occurs simultaneously with core collapse) preceding the emission of visible light (which occurs only after the shock wave reaches the stellar surface). At 7:35 a.m. Universal time, Kamiokande II detected 11 antineutrinos, IMB 8 antineutrinos and Baksan 5 antineutrinos, in a burst lasting less than 13 seconds.
In this respect, a point that deserves to be stressed is that all 3 detectors observed a relatively large number of events in the first one second of data-taking, about 40% of the total counts (6 events in Kamiokande-II, 3 events in IMB and 2 events in Baksan), while the remaining 60% were spread out over the course of the next 12 seconds.
In other words, these neutrinos travelled a total distance of 5.3 X 10^12 light seconds (168,000 light years), with almost half originating at roughly the same time (within about a 1 second burst of neutrino emission), and all arrived at earth (the light-transit time of earth's diameter is << 1 second and is not a factor due to the spacing of the detectors) within about 1 second of each other. In other words, they all travelled at close to the same speed to within nearly 13 orders of magnitude (5.3 X 10^12 seconds/1 second), far greater than any other measurement precision ever made for the speed of light. And, they all travelled at very close to the speed of light (travelling the same distance as the photons that reached Earth 3 hours later) at a speed consistent to c to within about 1 part per 500 million).
One would expect that since the neutrinos are emitted with potentially a range of energies, that their transit time would have exhibited a range of speeds (all in the 0.9999+ c speed range) if they were sub-luminal particles. While it has been believed that because the total ârest-energyâ of a neutrino is on the order of a few eV, while the rest-mass of an electron is about 511 KeV, neutrinos would all travel at close to c if they have mass and high-energy. But the energy they carry is sufficient to bring their speed to near c to only about .999999+ c if they are mass-particles, and the range in energies from pair-production should produce a spread in those speeds, albeit at many significant figures beyond the first few 9s. The calculated energy is indeed high, but not infinite. But that is not what was observed. They were observed to have all travelled at the same speed to 13 significant figures. In other words, had they had slight variations in their speed all slightly less than c, they would have had a large spread in the arrival time at Earth, on the order of days to years. The actual observation is far more consistent with neutrinos as having zero rest mass, and traveling at c, and appears wholly inconsistent with having a rest-mass and ejected with a spectrum of varying energies.
Let us briefly review the history of the discovery of neutrinos.
Historically, the study of beta decay provided the first physical evidence of the neutrino. In 1911 Lise Meitner and Otto Hahn performed an experiment that showed that the energies of electrons emitted by beta decay had a continuous, rather than discrete, spectrum. Unlike alpha particles that are emitted with a discrete energy, allowing for a recoil nucleus to conserve energy and momentum, this continuous energy spectrum to a maxium energy was in apparent contradiction to the law of conservation of energy and momentum for a two-body system, as it appeared that energy was lost in the beta decay process, and momentum not conserved.
Between 1920-1927, Charles Drummond Ellis (along with James Chadwick and colleagues) established clearly that the beta decay spectrum is really continuous. In a famous letter written in 1930, Wolfgang Pauli suggested that in addition to electrons and protons, the nuclei of atoms also contained an extremely light, neutral particle. He proposed calling this the âneutronâ. He suggested that this âneutronâ was also emitted during beta decay and had simply not yet been observed. Chadwick subsequently discovered a massive neutral particle in the nucleus, which he called the âneutronâ, which is our modern neutron. In 1931 Enrico Fermi renamed Pauli's âneutronâ to neutrino (Italian for little neutral one), and in 1934 Fermi published a very successful model of beta decay in which neutrinos were produced, which would be particles of zero rest mass but carrying momentum and energy and travelling at c, or very low-mass particles traveling at nearly c.(3)
Before the idea of neutrino oscillations came up, it was generally assumed that neutrinos, as the particle associated with weak interactions, travel at the speed of light with momentum and energy but no rest-mass, similarly to photons traveling at the speed of light with momentum and energy but no rest-mass and associated with electron-magnetic interactions. The question of neutrino velocity is closely related to their mass. According to relativity, if neutrinos carry a mass, they cannot reach the speed of light, but if they are mass-less, they must travel at the speed of light.
In other words, in order to conserve both momentum and energy during beta decay, the theoretical particle called a 'neutrino' was predicted. It was presumed that the neutrino either travelled at the speed of light and had zero rest mass (most dominant theory until the 1980s) but momentum (analogous to the electromagnetic photon, which travels at the speed of light, with momentum, but with zero rest-mass), or else it travelled at near-relativistic speeds with very small rest-mass (the less popular and unproven theory).
However, with the apparent recent discovery of neutrino oscillation, it became popular though not universal to assert that neutrinos have a very small rest mass: "Neutrinos are most often created or detected with a well defined flavor (electron, muon, tau). However, in a phenomenon known as neutrino flavor oscillation, neutrinos are able to oscillate between the three available flavors while they propagate through space. Specifically, this occurs because the neutrino flavor eigenstates are not the same as the neutrino mass eigenstates (simply called 1, 2, 3). This allows for a neutrino that was produced as an electron neutrino at a given location to have a calculable probability to be detected as either a muon or tau neutrino after it has traveled to another location. This quantum mechanical effect was first hinted by the discrepancy between the number of electron neutrinos detected from the Sun's core failing to match the expected numbers, dubbed as the "solar neutrino problem". In the Standard Model the existence of flavor oscillations implies nonzero differences between the neutrino masses, because the amount of mixing between neutrino flavors at a given time depends on the differences in their squared-masses. There are other possibilities in which neutrino can oscillate even if they are massless. If Lorentz invariance is not an exact symmetry, neutrinos can experience Lorentz-violating oscillations."(4)
Thus, observed oscillations in 'flavor' (type of neutrino based on origin source) suggested that neutrinos had a small rest mass, and therefore according to Einstein had to travel at less than c.
But do they?
"Lorentz-violating neutrino oscillation refers to the quantum phenomenon of neutrino oscillations described in a framework that allows the breakdown of Lorentz invariance. Today, neutrino oscillation or change of one type of neutrino into another is an experimentally verified fact; however, the details of the underlying theory responsible for these processes remain an open issue and an active field of study. The conventional model of neutrino oscillations assumes that neutrinos are massive, which provides a successful description of a wide variety of experiments; however, there are a few oscillation signals that cannot be accommodated within this model, which motivates the study of other descriptions. In a theory with Lorentz violation neutrinos can oscillate with and without masses and many other novel effects described below appear. The generalization of the theory by incorporating Lorentz violation has shown to provide alternative scenarios to explain all the established experimental data through the construction of global models."(5)
If they have a rest mass, and travel at near-c but slightly below c, there should be a slight variation in their speeds based upon their total energy (most of which would be kinetic energy, not rest-mass energy). In other words, various high-energy neutrinos would travel at, for example, .99999997 c or .99999995 c, etc., and this variation in speed, however slight, should be detectable.
But the variation in neutrino velocity from c, in the SN1987A data, was at most about 1/490,000,000 (3 hours/168,000 years). It was actually much closer to c than that (and most likely at c) because of the head-start the neutrinos received over the photons. More importantly, their close arrival time (40% arrived within 1 second) implies an identical speed to 13 orders of magnitude. While they are all released as essentially prompt neutrinos, the remaining energy of the core implosion should have taken a significant amount of time to churn through the overlying massive amount of star. While one might argue that it would take less than 3 hours for the core implosion energy to reach the surface of the star, and then start its race to Earth with the previously released neutrinos, I believe this has been fairly well presented previously in the astrophysics community to be a reasonable value.
The calculations for the volume of the star that actually underwent core implosion shows such a volume at about 60 km diameter, or about 1/100 light-second, and would not have been a factor in the timing of the arrival of the neutrinos.
Most of the neutrinos released are not from the proton/electron or positron/neutron fusion releasing electron neutrinos and anti-neutrinos. Rather, the energy of the degeneracy creates neutrino/anti-neutrino pairs of all 3 flavors, which travel in opposite direction (to conserve momentum). Most of the neutrinos released were therefore from this pair-production, which would have occurred relatively simultaneously (to within a few seconds) within the volume of that imploding core.
So, the spread in arrival time of the neutrinos on Earth, measured at 13 seconds, is accounted almost entirely due to the time for the pair-production and cooling to be completed. In other words, all of the neutrinos that travelled those 168,000 light years travelled at exactly the same speed without regard to their energy to within 13 orders of magnitude.
So the 1987a data show both an extreme example of exactly the same flight of time without regard to energy, and a speed almost exactly equal to c to within far better than 1/500,000,000 based on the 3 hour discrepancy of the early arrival of the neutrinos compared to the photons after travelling for some 168,000 years.
This data strongly suggests that neutrinos travel at light speed with energy and momentum, but no rest mass, as originally surmised; and not at slightly below c with some slight rest-mass, as has been the notion as of late (since flavor oscillation was recently detected).
The two notable facts from this discussion: The SN1987A neutrinos all travelled at identical speed to within 13 orders of magnitude of precision; and they all travelled at every near to light speed (arriving 3 hours earlier than the photons) to 1 part per 500,000,000 or less. The 3 hour 'early arrival' can be attributed entirely to the estimated 3 hours for the core-implosion energy to churn to the surface of the star, starting the race with the neutrinos which had an approximately 3 hour head-start.
Accordingly, this evidence strongly suggests that neutrinos travel at a constant speed with regard to their energy, and that that constant speed is c.
Quotations and References from below:
(1) http://en.wikipedia.org/wiki/Supernova_1987A
(2) Improved analysis of SN1987A antineutrino events. G. Pagliaroli, F. Vissani, M.L. Costantini, A. Ianni, Astropart.Phys.31:163-176,2009.
(3) http://en.wikipedia.org/wiki/Beta_decay
(4) http://en.wikipedia.org/wiki/Neutrino
(5) http://en.wikipedia.org/wiki/Lorentz-violating_neutrino_oscillations
Steve:
Their ML estimator has one parameter - the TOF - but what it minimizes is the difference the target and source distributions. The estimator starts with the assumption the source and target distributions aren't quite matching due to noise. The noise includes both TOF error and sampling bias. They hold one value - TOF error - constant (ie they assume a specific value for the time-of-flight delay), and measure the skew in the target distribution vs the source distribution. The joint probability of the data
PI (x_i) is a direct measure of the option 3 bias. They measure which value of TOF gave them the smallest bias - the largest PI (x_i).
The approach is invalid only if PI (x_i), the joint probability of the data assuming it is from the source distribution, somehow doesn't represent the bias in the sampling (the bias in how neutrinos are dropped midway). If the source distribution is flat, that is uniform, then, yes, biases such as dropping all of the tail end of the distribution won't be caught by the estimator. But they are highlighting the peaks in the source waveform - these non-uniformities there will make an ML estimator reduce the joint probability for many types of biased drops.
One cannot just add more parameters to an ML estimator to capture things such as the skew in sampling, since the resulting optimization curve often has multiple maxima (local maxima), making the procedure arbitrary.
James, Daedalus2u,
Their smoothing of the high-frequency oscillation is just for calculating the source (proton/source-neutrino) probability distribution. They do not smooth the neutrino detection time at the OPERA end, just the times on the CERN side. There is nothing wrong with that - in measured data there is rarely ever an exact probability distribution.
I don't claim their result is valid; not being a physicist I am not qualified to tell. But their statistics are as solid as those in many other published papers - one can't
rule out their experiment on statistical issues.
A K (Ajoy) - By smoothing over and/or discarding waveform observations the researcher have masked actual conditions effecting OPERA event test results.
Figure 9.7 of the referenced Brunetti thesis shows "Waveform functions superimposed on the OPERA events of the final data sample..." To my experienced eye, the smoothed waveform data is aligned with oscillating OPERA events!
This indicates to me that actual experimental conditions that producing the oscillations both in the original waveform and OPERA data!
In all cases it clearly appears that the extraction runs begin with a slowly increasing number of events that peak at around 7,500 ns into the run, then the number of events drops precipitously (these waveform observations are discarded).
At about 8,000 ns into the run the oscillations began in the original waveform observations, increasing in magnitude as the extraction progressed. I can't determine from viewing the infrequent opera event observations whether they also increase in magnitude, but the oscillation of OPERA events is apparent, most strikingly in the second extractions.
None of these effects apparent in both the CERN proton distribution 'waveform functions' and OPERA events reveal that experimental conditions are have direct effects on the
test results.
Why, in all experiments illustrated do events generally begin to increase as the extractions progress, then become erratic after about 7,500-8,000 ns? These effects have not been considered by the researchers (according to this thesis document), but they certainly appear to be effecting test conditions and results.
IMO, these effects are not just insignificant statistical effects - they bring basic experimental procedures into serious question.
A K (Ajoy) - My more complete response is being help for review... By smoothing over and/or discarding waveform observations the researcher have masked actual conditions effecting OPERA event test results.
Figure 9.7 of the referenced Brunetti thesis shows "Waveform functions superimposed on the OPERA events of the final data sample..." To my experienced eye, the smoothed waveform data is aligned with oscillating OPERA events!
Please examine for yourself if the OPERA events do not exhibit the oscillations omitted from the 'waveform function' data - indicating some unexplained conditions effecting all experiments.
What is the last on this? My head is going to burst with anxiety...
The oscillations they smoothed were at 30/60 nsec period. The X-axis tickmarks in the figure you cite are 2500 nsec apart. My eyes can't resolve patterns repeating at distances of 1/40th of that tickmark, especially where the data are just a scatterplot with no connecting curve.
The beauty of random data is if one stares long enough, one sees whatever pattern one wants to in it.
As to why the proton distribution gets more complex at 7500 msec, I guess only a physicist can answer. Is there a reason why the proton distribution can't be that way? The earlier MINOS paper shows its own proton PDF distribution, with arbitrary squiggles between the two edges. Did anybody ask them to explain the squiggles? Extraordinary claims require extraordinary evidence; they do not have to answer extraordinary objections.
And when objections get more complex than the original explanation, one begins to believe the original explanation.
all these sure is interesting but i don't understand how everyone seem to be relying on this to prove that travelling faster than speed of light is possible, when according to my personal work, i have come up with a 90% brobability.( escuse if is not speel right) that travelling faster then speed of light is possible...
I really liked this Article / explanation. I am curious to put my hands on the raw data, as statistics and crunching numbers is what I do for living. Do you any idea how I can get acces to the raw data? Would be interesting if they made the typical amateur mistake of applaying Normal distribution statistics on non Normal distributed data. That alone can give 20 per cent error.
A K (Ajoy) - Nonsense! There is no 'random' data illustrated in the charts I referenced - it has all been produced by measured indicators of processes used to detect particles. That data is being used to relate the process detecting extracted protons to the expected probability of detecting neutrinos, whose detection is also charted. The purpose of charting data is to enable its visualization and the potential identification of patterns within the data that has not be previously analyzed.
In the Fig. 11 chart in the official OPERA report, the data points representing neutrino detections generally alternate by nearly 20 "Events.150 ns". Such a pattern can be generally described as an 'oscillation'.
The more general initial pattern of an initial increasing volume of events occurs over roughly the first half of each extraction. Fortunately, this pattern should be apparent to most reasonably intelligent people who view the chart without mathematically analyzing the data to quantify a trend line of some specific slope.
That this initial trend is disrupted by a sudden event or change of experimental conditions occurring about midway through all extractions is obvious.
Your objections to this analysis are pooh pooh!
Since the charted events are indicative of changing conditions of proton detections very near the neutrino beam source, they indicate changing patterns of conditions occurring within the neutrino beam. Something is producing those patterns - the changing conditions within the neutrino beam eventually being extraordinarily described as FTL should be meticulously understood since an exceedingly complex series of inferences is being used to support that claim!
The first solid objection to the results has surfaced. The cesium atomic clock might have had its time shifted from the CERN reference not because of the journey but because of difference in gravity, per some GR equations. This drift would have accumulated till the device was unpacked and set up. I am not sure where and how the Opera team is responding to objections, so don't know what the status of this is.
Hmmm, doesn't look like they depend on a synchronized clock. They get their nano-sec accuracy by using GPS 'common view' - ie looking at the signal from commonly-visible satellites at the two places. The cesium atomic clocks don't have to be synchronized. At 40 nsec per 4 days, the GR time dilation looks way too small to matter at the extraction timescale of 100s of microseconds.
We are back to square one.
Based on charts illustrating the numbers of proton and neutrino detections indicating, in particular, a destabilization of proton and neutrino beam conditions occurring following a peak in detections ~6,000 ns for first extractions and about ~7,000 ns into each extraction run, I strongly recommend that only data representing stable beam conditions prior to those peaks be selected for analysis. Please see my preceding comments for further explanation.
If final neutrino ToF results produced from selected stable beam data substantially contradict the analysis of the complete set of extraction duration data, especially if the stable beam data does NOT indicate FTL neutrino flight times, the current FTL conclusion would have to be reconsidered as a product of beam conditions.
If the subset of stable beam data confirmed the FTL conclusion it would be to some extent substantiated.
Since this approach does not require any additional experiments, it can be undertaken by selecting data and reanalyzing results.
Before anyone is continuing to speculate over superliminal velocities, I would like to point
out something interesting...
Determination of the CNGS global geodesy
http://operaweb.lngs.infn.it/Opera/publicnotes/note132.pdf
To get the exact point on the surface of earth, we need to know the position
of the GPS satellites for a given time and their distance from us. No problem so far,
GPS is able to provide us with that information.
The authors used the Bernese software which is available under
http://www.bernese.unibe.ch/
There are some kinds of problems which will be further points of investigation
if my first suspicion is incorrect.
One problem: You will normally compile Bernese yourself and it is a known problem
that FORTRAN compilers are very different in their quality to numerical
problems. The second problem is that FORTRAN constants are stored in REAL
precision (6-7 digits) if you are not declaring them. Anyway...
Lets imagine a programmer did the marginal error of not using the correct
reference ellipsoid value of 6 378 137 m, but the abbreviated version
6 378 000 m.
What will be the influence on the GPS precision ? Practically *NOTHING* because
the satellites are symmetrically around the earth and position accuracy is very insensitive against
height changes if the distance between sender and receiver is long enough.
For example, to get a 18 m change for a distance of 730 km you need a height difference of
5 km !
So the values are in fact accurate concerning the position and noone will see a problem,
the software is reliable.
But what if you want to know the *distance* between two points on earth ? Having a slightly
smaller value has the effect that the calculated distance is smaller than the actual distance.
How much ?
730534.610 km * ( (6 378 137 /6 378 000)-1.0) = 15.7 m
15.7 m / 299 792 458 m/s = 52.3 ns
Opera difference: 53.1 and 67.1 ns
Strange coincidence, isnt it ?
all very well and interesting but...
TSK - They should be able to calibrate their gps system (and code) by comparing it to 'actual' shorter distances measured with 'real' mesurement tools, lets say over 1 to 10 km.
Hi Chelle,
while the missing line can in fact be coincidence (or not) I have found out something which is much more interesting.
In http://operaweb.lngs.infn.it/Opera/publicnotes/note132.pdf
the authors of "Determination of the CNGS global geodesy" published
their results in the ETRF2000 system:
X Y Z
T-40-S-CERN 4394369.327 467747.795 4584236.112
A1-9999 4582167.465 1106521.805 4283602.714 (Table 6)
What does this mean ?
All values are in meters and give the distance to the barycenter of the earth in a specific direction. The X-coordinate is the distance of the point in direction of the equator/greenwich meridian point, the Y-coordinate the distance of the point in direction of 90°E and 90°W
and the Z-coordinate the distance in direction of the poles.
Explained in detail in
http://en.wikipedia.org/wiki/ECEF
Because I wanted to control the position in regards to geodetic
latitude/longitude/altitude, I wrote a program to calculate
the position to sub-meter precision.
(see http://en.wikipedia.org/wiki/Geodetic_system)
The output:
Latitude Longitude Altitude
T-40-S-CERN 46.242434 6.0758306 429.70
A1-9999 42.453675 13.576122 1012.33
The ITRF website claims that the ITRF is identical to WGS84
to one meter:
ftp://itrf.ensg.ign.fr/pub/itrf/WGS84.TXT
The WGS system has differences to an equipotential (same height) due to gravitational differences (geoid undulations), but both the Gran Sasso Tunnel and Geneva have nearly equivalent geoid undulations:
Gran Sasso Tunnel (Paper, Fig. 5): approx. 48 m
Geneva : 49.833 (http://www.unavco.org/community_science/science-support/geoid/geoid.html)
Now the comparison:
Gran Sasso labor: 962 m N.N.
Location in Geneva: 425 m N.N. (Google Maps,(46.242474, 6.075792)
Depth of CERN in paper: 140 m
Difference: 677 m
Difference in height according to the ITRF coordinates:
1012.33 and 429.70 = 582 m
Something is wrong with the measurement.
hi TSK,
i offered your thoughts to some other guys on the blog RelativKritisch. if you're interested in further discussions, have a look.
regards, galileo2609
Excellent article. I"m a PhD student in another discipline, understand all about statistical error, and found your discussion of this in your discipline fascinating and understandable.
Will be very, very interesting to watch this as the discussion goes on. It seems like the speed of light is one of the immutable constants of the cosmos, but then, that is based on best observation and critical review. Time will only tell. (No pun intended) :)
We already have faster then light travel, Einsteins "spooky action at a distance" where one twinned particle reacts instantaneously to a change in the other particle. The argument that no information is transmitted is just semantics-the particles behave as if the space between them is nonexistent-perhaps for them, in some way it isn't. This world require a new understanding of the universe, we have space time (the expanded universe) and a different kind of space where what we think of as distant particles are contiguous. What is this new space, or geometry of space, are all particles part of it or only twinned particles?
The error is clear.
Read http://static.arxiv.org/pdf/1109.4897.pdf
They did discard invalid PEW's, i.e. PEW's without an associated event, but they did not discard invalid samples in the valid PEW's, i.e. samples without an associated event. As a result, virtually all samples in the PEW's are invalid.
This can be tolerated if they are ignored at the Maximum Likelihood Procedure.
However, the MLP assumes a valid PDF and because the PDF is constructed by summing the PEW's the PDF is not valid: the effect of summing is that all valid samples are buried under a massive amount of invalid samples.
which makes the PDF not better than a PDF which is constructed only with invalid PEW's
This is a monumental and bizar error.
Why is it that all these scientists were not missing the missing
probability data or did not
stumble over the rumble in the PDF used by the data analysis?
For a more formal proof:
http://home.tiscali.nl/b.morrien/FTL/ProofOfWrongAnlysisOperaCollaborat…
Bert Morrien, Eemnes,The Netherlands
In Giulia Brunetti's PhD Thesis, which I found online, he describes an 8 MHz lowpass filter in the output of the beam current transformer used to measure the proton bursts generated at CERN.
This lowpass filter is not mentioned in the OPERA/CNGS Neutrino Velocity paper. I wonder whether it was in use when the measurements were made.
If it was in use, I wonder how they compensated for the delay of this filter. A lowpass filter will have a delay which varies with frequency in the passband. Therefore, it may not be adequate to represent its delay by a single number, unless it was quite well delay equalized. The neutrino velocity paper describes delays of various items by a single number.
The correlation later performed will be quite sensitive to the delay introduced by this filter into the high frequency components of the signal, not only in the passband, but perhaps some distance into the stop band.
Perhaps it would be appropriate for the team to publish the details of this filter, specifically its group delay and attenuation characteristics vs frequency, and the calibration methodology surrounding it.
How well delay equalized is this filter?
How did they measure its delay?
Is this filter in software or hardware? If it is in software, do they still have the raw unfiltered data?
References:
http://operaweb.lngs.infn.it:2080/Opera/ptb/theses/theses/Brunetti-Giul…
http://arxiv.org/ftp/arxiv/papers/1109/1109.4897.pdf
The reason why Einsteinâs Cosmological Constant is Wrong
The reason why the Cosmological Constant is wrong is because Einstein thought his Theory of Relativity described everything that existed. The explanation to why Einstein was trying to discredit Quantum Mechanics is because he did not know his Theory of Relativity could not be applied to subatomic particles. Since it is evident that the neutrino is a subatomic particle, I cannot figure out why so many scientists believe that it could be defined by the Theory of Relativity? It is evident that the neutrino can only be described by the laws of Quantum Mechanics.
Theory on Gravity
A while back I predicted that it was possible for particles to travel faster than the speed of light, in which this information was published in 2007, in a book called Ronald Newman's Theory on Everything. At the time when I made this prediction that contradicts Einsteinâs cosmological constant, I also said that the LHC might be able to push particles so fast that this would cause these objects to start veering in different directions and spinning around in a circle. The reason why I believe extreme acceleration can cause particles to start veering in different directions is because of the way in which our universe is constructed. Because our universe contains a force that pushes against all objects, this is why all the bodies throughout our universe have formed into galaxies. Since this force that pushes against objects is continuous throughout our entire universe, I will call it the perpetual force. The reason why accelerating particles can cause them to start veering in different directions is because this prevents the perpetual force from being able to push particle in one precise direction. Evidently the LHC pushes particles in a circular pattern, which is why we are able to observe many course changes at the exact moment when a particle outruns the perpetual force.
Ronald Newman
Thank you very much for this superb article.
One thing that many people overlook is that while the "received" theoretical framework should help us, it should not be the final criterion to decide what is right and what is wrong. That prerogative should be left to empirical experiments.
Johnson C. Philip, PhD (Quantum-nuclear Physics)
http://www.Physics4u.info