"A constant struggle, a ceaseless battle to bring success from inhospitable surroundings, is the price of all great achievements." -Orison Swett Marden
One of the greatest assumptions we make in our study of the laws of nature is, well, that they're laws of nature, not particularly special to where or when we happen to be looking at them.
Image credit: NASA & ESA.
Whether we look on our home planet, within our own galaxy, at a relatively nearby galaxy (like NGC 4522, above), or at galaxies extremely far away (faintly visible in the background), we always tend to assume that the fundamental laws that govern the Universe don't particularly care about where or when you measure them.
But they might.
Image credit: 2-degree Field Galaxy Redshift Survey.
The reason we assume the Universe has the same laws and the same fundamental constants everywhere -- at all times and in all directions -- is because it looks like it's obeying the same laws everywhere!
Image credit: ESO / P. Grosbøl.
Galaxies follow the same clustering patterns in all directions, exhibit the same gravitational phenomena, and show similar internal dynamics no matter where or when in the Universe we look. If they didn't, we might start to question whether either the laws of gravity or maybe even the fundamental gravitational constant, G, varied in either time or space.
Similarly, if electromagnetic or quantum phenomena appeared to vary over space or time, or be significantly different in one direction over another, we might worry about our electromagnetic and quantum laws and/or constants.
Image credit: WMAP / NASA / WMAP science team.
From constraints in the cosmic microwave background, we can show that -- from when the Universe was 380,000 years old until today, where it's 13.7 billion years old -- the speed of light could have varied by no more than 4%, a very impressive constraint!
There are a number of good theoretical reasons to expect that the fundamental constants, Planck's constants, the speed of light, and Newton's gravitational constant, really are constant. But it's always conceivable that there is some sort of small variation -- either in time or space -- to these parameters. The only way to know for sure is to measure them.
So, how can we do that? In principle, it's simple.
Image credit: Szdori, OrangeDog and WikiMedia Commons.
The most common element in the Universe is hydrogen; by number, over 85% of the atoms in the Universe are hydrogen, even after you account for 13+ billion years of stars burning their hydrogen fuel through nuclear fusion! As shown above, the fundamental atomic transitions of hydrogen are well-known. So, you'd imagine, if we can measure hydrogen's spectral lines in every direction, and we can do it at a variety of distances (and hence a variety of lookback times), we can see whether these fundamental constants determining these frequencies have changed or not.
But in practice, there's something we can do that's even better.
Image credit: Fabry-Pérot interferometer/étalon fringes, by John Walton.
Because there's not only the basic atomic structure of hydrogen, there's also more advanced, subtle signals that comes from hydrogen atoms. In particular, I'm talking about fine and hyperfine structure in the atomic transitions of hydrogen and its heavy, stable isotope, deuterium.
Image credit: DJIndica of WikiMedia Commons.
Well, the person who helped devise the best technique to measure this fine structure at high redshift -- and is arguably the world's leading expert on it -- is Australia's John Webb. The fine-structure constant is actually a combination of a few well-known constants, including the electron charge, Planck's constant, the speed of light, and π. If one of them were changing (presumably not π), this would be very big news! And the reason to get excited about the fine structure constant is that it's been measured so precisely. Specifically, the fine-structure constant, α, is:
Now, what Webb does -- and he's been doing it since before I started graduate school -- is he takes the best spectra of quasars I've ever seen. In particular, he looks at absorption lines from the intervening hydrogen gas clouds in between the quasar itself and us. Here's an example from a 2002 paper of his.
Image credit: M. T. Murphy, J. K. Webb, V. V. Flambaum, and S. J. Curran.
From these spectra, if the fine-structure constant was truly constant, one would expect to get the same signature for it from all of these absorbing hydrogen clouds. But that is not, and has not been, what Webb's team has been finding.
Image credit: Same team, different paper, from 2000.
What they find -- and what they've consistently been finding for more than a decade -- is that the fine structure constant appears to have been different, by a few parts in a million, in the distant past! The effect is small, but their error analysis has been checked, scrutinized, criticized, etc., and has been shown to be correct by multiple independent sources. To put it bluntly, they're doing science the way science is supposed to work.
Image credit: Same team, different paper, this time from 2002.
Even though terrestrial measurements show that it hasn't varied here over the past 4 billion+ years, that doesn't mean it isn't different elsewhere in the Universe, or wasn't varying at an earlier time, and has been constant only recently. Their data still needs to be explained.
Of course, this is highly controversial. At this point, it really does appear that the data, despite good reasons to be cautious, is robust. The most recent paper is available here, and all of the subsequent figures are taken from it. Including this one:
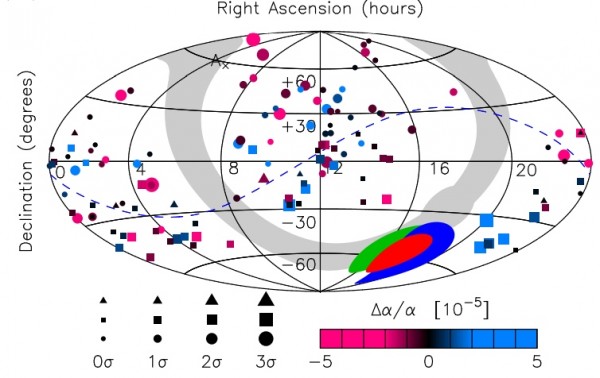
As you can see, there are actually much larger apparent variations -- up to about 50 parts in a million -- when individual systems are looked at. But these aren't spatially random variations. There's enough data to suggest that, even when random variations are taken into account, that one direction of the Universe has a preferentially higher value for this constant, while the opposite direction has a preferentially lower value. With hundreds of systems now measured by two different instruments, these results have not only been confirmed and held up over the past decade, the combined data is very strong (at about 5-σ significance), and that makes these results really annoying.
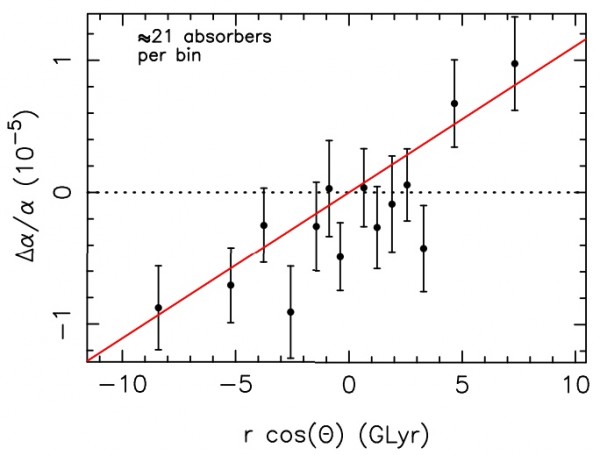
Why annoying? Because there isn't a good, simple explanation for this! So just what is it that's going on?
Well, John Webb recently wrote an article detailing these results, which is an interesting read. In short, he developed this new absorption-line technique 11 years ago, it's about 10 times better than any other technique we have for measuring this variation, and it sees a variation about 4-5 times larger than their errors. It varies across directions in space, it varies for both low-redshift and high-redshift gas clouds, and it cannot successfully be explained away by any known physics.
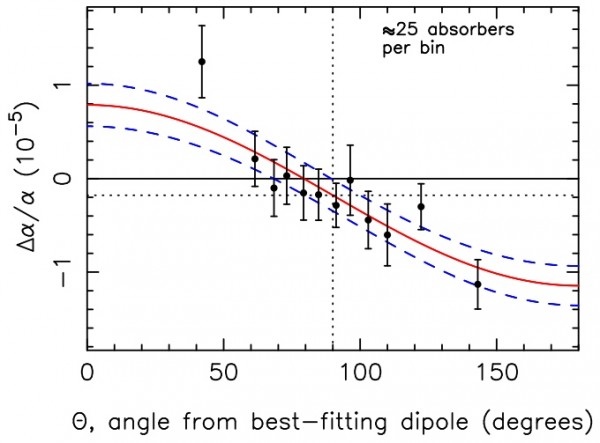
Theoretically, I don't have a good explanation for this. The ones I can think of that would cause this effect -- like segregated elements in these gas clouds -- aren't physically reasonable, much less well-motivated. From an observational point of view, there is at least one reason I can find to be concerned. The data comes from two instruments: the Keck Observatories and the VLT. Although the Keck data shows this highly statistically significant result at both low-redshift and high-redshift, the VLT data does not show it at low redshift, and shows a much less significant one (only three-σ, instead of four- or five-σ usually demanded) at high redshift.
The only thing I can say is the same thing the authors can say: maybe there's some sort of problem or error associated with this technique that we do not understand. If we only had the VLT data, we wouldn't think we were seeing anything of note; it's only the Keck data on its own or the Keck + VLT data combined that show a very strong result.
Because the implications are so alarming, I would demand -- just as I did for the alleged faster-than-light neutrinos -- extraordinary evidence to back up this extraordinary claim. What would that extraordinary evidence look like? I give John Webb full points for identifying the exact two things I would want in his latest paper:
Future similar measurements targeting the apparent pole and anti-pole directions will maximise detection sensitivity, and further observations duplicated on 2 independent telescopes will better constrain systematics. Most importantly, an independent technique is required to check these results.
Now that they've identified the directionality of this variation in the fine-structure constant, you want to look, with multiple instruments, in those directions! If all the instruments you use see the same large, independent effect, you know it isn't an artifact of your instrument and it isn't due to the small number of sources (with large effects) you happened to measure in those directions so far.
So if you made those measurements and you still saw this big effect, you'd have every reason to be confident in what you've accomplished. But it could still be a bizarre artifact of this technique, even if you can't identify what, exactly, is going on. So you want to find an independent technique to check it with.
Image credit: L. Horne.
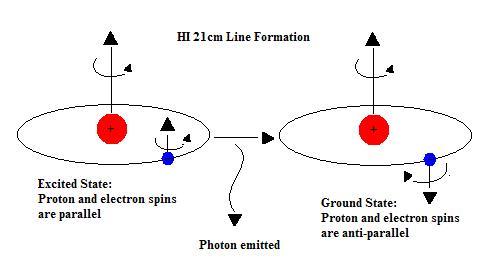
It's to use -- instead of atomic absorption lines -- an even more precise transition: the 21-cm Hydrogen spin-flip line! This has the potential to be even more accurate than Webb's technique down the road, and can measure intervening gas clouds as far back as the Cosmic Microwave Background, at a redshift of 1089. (Making what we call "high redshift" today -- a redshift of 3 or 4 -- look like bupkis!) But at this point, it can only constrain the fine structure constant to a few parts in 1000; to practically get the accuracy they'd want would require a much greater financial investment than is feasible.
Which is, perhaps, why Webb gives this depressing, but perhaps realistic, ending to his piece:
As I said at the start of this article, no-one believes us yet, and we are in for a long battle. Some days I doubt I shall be living when the proof comes in.
The work is technical, laborious, very difficult, requires a great deal of data from extremely expensive scientific facilities, and the analyses take a lot of time and effort.
But on other days I'm more optimistic and remind myself that, for now, I'm alive and kicking and working on it.
After all, this is an extraordinary claim, but it isn't a claim that's been made because anyone's done something crazy; it's a claim that's been made because someone's done something amazing, and is seeing something crazy! So it's definitely going to take some extraordinary evidence to put this on solid ground, but that's exactly what everyone involved in this issue is shooting for, and I can't wait to see how it turns out! (And a happy birthday to Carl Sagan, for those of you who caught the reference!)
- Log in to post comments
It's because of articles like this that I love this blog. So absolutely fascinating! The universe is a vast and interesting place, and it seems like it keeps getting MORE interesting!
âIf one of them were changing (presumably not Ï)...â
No - my money's on the 4.
Ethan Siegel wrote (November 9, 2011):
> The only way to know for sure is to measure [...]
Right. Measurement keeps a check on any assumptions, expectations, or models concerning the result of this measurement, or any results of such measurements; whether they might be based on results of any other (preceding) trials, or not.
> So, how can we do that? In principle, it's simple. [...]
> So you want to find an independent technique to check [...]
Apparently this applies to "techniques" with different (possibly mutually exclusive, or complementary) dependencies on several assumptions, expectations, or models.
But isn't there always a strictly model-independent, definitive, thought-experimental "technique" to start with ?
How, for instance, is some given particles's value of "α" (or of "e²") to be measured, at least in principle, without involving any stipulations about the corresponding value of any other particle and/or of the same particle in any other trials ?
(At least to me that doesn't seem simple.)
Great article! I didn't know about this "anomaly" in H absorption lines before today. Awesome!
A quote from Douglas Adams comes to mind :)
"There is a theory which states that if ever anybody discovers exactly what the Universe is for and why it is here, it will instantly disappear and be replaced by something even more bizarre and inexplicable. There is another theory which states that this has already happened."
Okay. I bite. Where's the Sagan reference?
Brendan: "Extraordinary claims require extraordinary evidence."
While Sagan's version is most popular, I think there should be some credit to both Pierre-Simon Laplace who said
"The weight of evidence for an extraordinary claim must be proportioned to its strangeness."
and David Hume who said
"A wise man, therefore, proportions his belief to the evidence"
and if you want to credit the wording then how about Marcello Truzzi who said
"An extraordinary claim requires extraordinary proof"
in 1978?
Right, like Edd, I wouldn't have necessarily attributed that to Sagan. But because the "Extraordinary claims require extraordinary evidence." quote is a direct Sagan quote, I suppose it should indeed be considered a Sagan reference. :)
Okay, almost totally off-topic, but as it was sort of raised.... Pi shows up everywhere, but is best known as the radius of a circle's circumference to its diameter. If the universe's topology is not flat, the radius of an enormous circle's circumference to its diameter may not be the 3.14159... we all know and love. Could this have anything at all to do with these measurements of other values that appear to depend on pi, and are measured at such great distances? I think we have constraints on the curvature of the universe, at least if we assume inflation; if we tweak pi in that formula within those constraints, might the new value match measurements without changing the other physical constants?
I strongly suspect the answer is that this is butt, but had to ask....
pi shows up in Einstein's field equations - the classic place to go for curved space in physics. pi's got to be more independent than that - I mean you don't go redefining the sum of the Liebniz formula ( http://en.wikipedia.org/wiki/Leibniz_formula_for_pi ) when you're in a strong gravitational field. It's a genuine mathematical constant, not something that changes depending upon your location, any more than the value of 2 changes.
In addition, the fine structure constant effects are the realm of atomic physics, and on the small scales of an atom the space is pretty much completely flat - curvature scales due to gravity and cosmology are way way bigger than an atom, so I don't see how that could cause the effects seen there even if the pi in the formula were of a variable variety.
"It's a genuine mathematical constant, not something that changes depending upon your location"
Except pi is the radio of the circumference to diameter of a circle and in a non-euclidian space, that can be different from the flat euclidian space answer.
Guess what happens near a strong gravitational field...
In addition, electrons (for example) are very light, but apparently no extent (it's smaller than any possible measure we can currently manage).
And gravitational field strength depends on the distance from the object to the center of gravity.
The constants are all rather odd, really.
We have evidence they haven't changed for billions of years.
Evidence for being immutable is an inference from that, no more.
Like I said, odd.
Nice summary Ethan. Good links too.
Certainly Webb and team are doing excellent research.
Let me offer a modest observation/question. I defer to Ethan and other experts.
FIRST MY OBSERVATION:
1)First, take a look at Webb's polka dot chart (pink & blues) above.
Do you see that dashed blue line running through that chart.
I assume that is the line that distinquishes the two directions, i.e. in one direction the universe is more pink, in the other direction the universe is more blue.
2) Now take a look at Ethan's post
WMAP year 7: We Know What We're Doing!, February 10, 2010
Look at the 3rd image in that post. This shows the universe with a curve through it. (That curve is the mirror image of Webb's curve. Of course Webb is in the southern hemisphere so maybe he draws the universe backwards.)
Then Ethan says, "This is really, really interesting, because the hot part is exactly 180 degrees in the opposite direction from the cold part! This would be exactly what we would see if we were in motion!"
"What if we subtracted that motion out? Well, for the first time in the high resolution, that's what WMAP allowed us to see. What do these tiny temperature fluctuations look like?" End of ethan quote.
Then we see the 4th image, that Ethan quote refers to. Voila the line disappears.
NOW MY QUESTION
Is it possible that Webb did not properly take account of motion in the way that WMAP researchers have had to take account of motion?
This is just a question because I really don't understand and I defer to Ethan and other experts.
I'm still trying to think about the multiverse post, wherein our universe is a 4-dimensional region embedded in a larger 4-dimensional space (yes? "... four is certainly [enough dimensionality] to describe and explain everything I've written above.") So (neglecting lightspeed limits if necessary) one could travel in any direction so as to leave the flat region and enter a region where inflation is still occurring? ...and fall off the edge, just like in the olde days.
So since we are unlikely to be in the center of our flat universe-region, might you not expect to see the kind of anisotropy this post is about???
Just foolish handwaving from here I'm sure. Thanks for being available.
I've heard the call go out from pseudo philosophical or post modern types, that science makes "several assumptions", and one of these that would completely BREAK science if they didn't assume it is consistent laws everywhere. I've never bought that. I'd thought that, should laws ever be different under some circumstances, science as a method is perfectly capable of working under that framework.
I've only ever been able to try and use some logical arguments against it, but you give concrete examples, numerous ones, of exactly how the consistency of physical laws can be tested. This post alone should be the nail in the coffin for that tired old claim.
@ DJ
Well, there certainly are some assumptions made that if wrong would completely break science. Like the assumption that the universe makes sense (as in is self-consistent and operates according to rules, not 'makes sense' in the way that QM doesn't). If that assumption is wrong, then it pretty much means that all of science is a farce that only appears to lead to understanding (to the point where we can make working computers but hey).
This is basically the assumption that Young Earthers are questioning when they say dinosaur fossils could have been put there by God to mislead us. But it doesn't have to be God; we could just live in a nonsensical universe that only seems to follow consistent rules sometimes. We assume we don't, because, well, that's the only thing that makes sense. :P
I dunno, if you're assuming our world as it is is the "nonsensical" world, it's been going strong on a long string of VERY convenient coincidences for a good long time, and even if we couldn't get to the "bottom" of the chaos, I'd say science has at least told us a lot about the virtual "pocket" logic we temporarily find ourselves in to be accurate to at least that extent. Doesn't seem like it "breaks" science completely.
Further, if we found ourselves in eternally swirling chaotic laws of unpredictability, we could at least observe that's the case, and science could at least provide THAT much of an observation, except that something like awareness, people like us actually thinking about such things, wouldn't be possible so it would be a moot point.
"So since we are unlikely to be in the center of our flat universe-region"
This is the problem with using english to explain maths...
An ant sitting on a spherical globe of the earth is ALWAYS to be in "the center" of his flat universe (since he can't dig down, nor fly up, his universe is flat).
But anyone else with a different point of view would say they are in the center of the universe.
How do you measure "the center" of something? You have to find the edges.
Not easy to do on an infinite land (a sphere has no edge, so you can walk infintely far and still remain on the surface). So everywhere is the center.
But there's no way he can travel in ANY direction that will get him to the center of the sphere.
@ Wow: "her"
The ants you'll see walking about are males.
Your ant is experiencing a closed 3-dimensional spacetime embedded in a (possibly infinite) 4-dimensional universe. I think Ethan said that he doesn't need even one extra dimension to do the multiverse math, which seems to imply that our non-inflationary region is continuous with inflationary space, as his (handwavy) graphic with the red X's. That is to say, edges.
Actually even if all that is true, I don't know that that would explain the results; inflation isn't supposed to affect the fundamental constants, is it? But one might expect space to be peculiar out near the transition zone.
I do wish I was better at math; so did Einstein. Oh well, vita brevis.
"I think Ethan said that he doesn't need even one extra dimension to do the multiverse math"
You do need those extra dimensions to call the universe flat, though.
I admit to having fewer math skills than the common goldfish. I cannot, however, see how the concept of "infinities" can be incorporated into any valid mathamatical statement regarding a finite universe. The above example of an ant experiencing a three dimensional universe "embedded" in a four dimensional universe, seems to imply that the ant's perception determines it's reality, but it is actually that "perception" which is limiting the ant's ability to comprehend the multidimension reality. Similarly, our perception (commonly accepted as four dimensional) does not impose any real limitation on the reality of the universe.
If other dimensions exist, besides our perceived spactial and temporal ones, then understanding many of the unanswered mysteries of science may depend on our identification of those facets of reality. Everything from the consistancy of fundemental forces, to the nature of dark matter and the solution to quantum entanglement may be unknown to us until we can think outside of the limitations of perception, much as the ant will never get to the center of the globe until it grasps the concept of digging.
There is another constant not mentioned by Prof. Siegel which governs the force between two electric charges, namely the permittivity of the vacuum (epsilon(0)) which is hidden because it is equal to 1 in natural units.
Physics Constants Vary Between Galaxies Clusters
A. Fundamental Constant May Depend on Where in the Universe You Are
http://news.sciencemag.org/sciencenow/2011/11/fundamental-constant-may-…
B. From: EOTOE, Some Implications (I)
http://universe-life.com/2011/10/07/eotoe-some-implications-i/
PS1: (notes since 2005-6)
- Definitely: Dark energy and dark matter YOK! Universe's m reconverts to E at a constant rateâ¦
- Universe accelerated expansion is per Newton's motion laws, obviouslyâ¦
- Also, universe physics constants should vary, probably slightly, between galaxies clusters due to different clusters sizes...
- Also, the clusters formed by dispersion at inflationâ¦
Dov Henis (comments from 22nd century)
http://universe-life.com/
@18 & @19
Most worker ants are female. Of course the queen ant pretty much monopolizes reproduction.
The drones (males) in a colony are few in number. But even the males sometimes reproduce, "males produce clones by a process where a diploid egg loses its maternal contribution to produce haploid males that are clones of the father"
Insects are strange and stranger.
> Most worker ants are female.
Reading WP:
> These larger colonies consist mostly of sterile wingless females forming castes of "workers", "soldiers"
OK.
Neat article! I have to admit I've often wondered why some constant or other should be "absolutely" fixed. It reminds of the absolutely straight line that doesn't appear in nature!
As I read your post, Ethan, the image I got was a freshly-mowed lawn. Looked at from the backdoor, it looks like all the blades of grass are of equal height. But if you start to measure the height of each individual blade, you will find they vary - not by much and sometimes for different reasons. That clump of grass may be slightly thicker than another patch, or the soil might be a millimeter or so higher or lower for 6 inches - not enough to affect the uniformity of the cut, but enough to measure if you stick a ruler against the grass. You'd more easily see it if the wheels of the mower rode in the bump or hollow, but not if only the cutting blades passed over that small section. And so on.
I'm fairly sure the analogy breaks down pretty quickly. But I thought I'd share it as I procrastinate... :-)
I think I have an explanation for this. I remember seeing the following entry in the guest book of the Jadwin Hall physics building at Princeton in 1982 or 83:
Name: God
Time in: 9:00 AM
Time out: 9:05 AM
Comment: I changed the fine structure constant. Ha ha.
Maybe they are not. I've suspected the Fine Structure Constant for years, and figure it's an English plot. (Details available). For a fundamental constant it is too complex.
The universe has only a few dimensions, such as length and time. Even those merge into general relativity's ds distance dimension. GR was absolutely necessary for proper functioning of the GPS system, and independently verified by a separate long-term test involving orbital gyroscopes.
Time will tell.
All of them are. Drones don't work. To find male workers (including soldiers), you have to look at termites â and termites are cockroaches, not ants.
Like the assumption that the universe makes sense (as in is self-consistent and operates according to rules, not 'makes sense' in the way that QM doesn't).
That's not an "assumption," that's a conclusion that we can draw, based on the observation that (AFAIK at least) the Universe always seems to operate according to the same set of rules from one year to the next.
This over-mis-use of the word "assumption" is a pet peeve of mine. Creationists and other anti-rationalists try to pretend science is no better than religion because it's all based on certain "arbitrary" "assumptions," which they never actually specify. If they ever specified the "assumptions" all science is allegedly based on, they'd all be found to be CONCLUSIONS or OBSERVATIONS instead, and their whole con-game would fall apart.