"Alas! must it ever be so?
Do we stand in our own light, wherever we go,
And fight our own shadows forever?" -Edward Bulwer-Lytton
Ever since it was conjectured that the speed of light was the ultimate speed limit of the Universe, we have tried -- with the most powerful of our tools -- to push as close to it as possible.
Image credit: Sven Geier, retrieved from Alpha Centauri.
And we know the speed of light in vacuum -- in perfectly, completely empty space -- exactly: 299,792,458 meters-per-second. That's what we refer to as c, or more casually, the speed of light. And that's really exact, 299,792,458.00000000... (etc.) meters-per-second.
Image credit: CERN neutrinos to Gran Sasso.
And until the recent hullaballoo about neutrinos, in which one experiment claims that they can go about 0.002% (or 6,000 m/s) faster-than-light, we've never observed matter moving at or above the speed of light.
Image credit: NASA, ESA, K. France, P. Challis and R. Kirshner.
The previous "best measurement" we had on neutrinos was from this supernova, above, which confirmed that neutrinos move at speeds indistinguishable from the speed of light, to an accuracy of ±0.62 meters per second.
But we've spent generations trying to accelerate matter as close to the speed of light as we possibly can under extremely controlled laboratory settings. And although it was never the goal of any of these experiments, it's one of those serendipitous results you get for free. Here's how.
Image credit: Carel Vandertogt of paradox-paradigm.
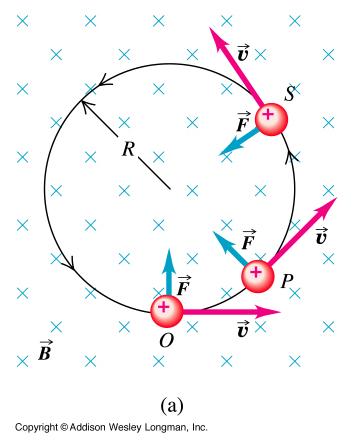
One of the most basic properties of charged particles is that if you place them in an electric field (E-field), they experience a force and accelerate. Positively charged particles accelerate in the same direction as the E-field, while negatively charged ones accelerate with the same magnitude, but in the opposite direction.
Charged particles, once they're moving, also respond to magnetic fields.)
Image credit: Addison-Wesley Longman, retrieved from physics.sjsu.edu.
If you orient a magnetic field perpendicular to a charged particle's velocity, it will bend its orbit into a circular shape, with positively and negatively charged particles bent into opposite directions (clockwise/counterclockwise) from one another.
And if you combine these two properties in the right configuration, you can accelerate these particles in a circular path!
Image credit: Sandbox Studio, retrieved from symmetry magazine.
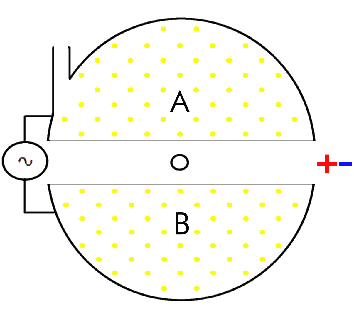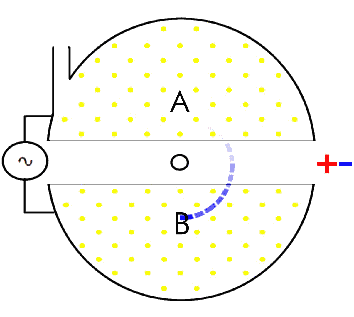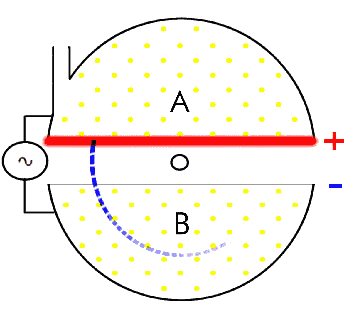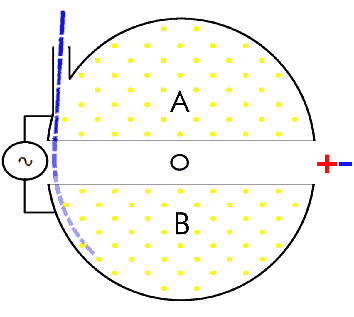
This is a primitively designed cyclotron, predecessor to the great ring-shaped particle accelerators of the modern day.
In this early design, you'd have a magnetic field that bent your charged particles into a circular path, but every time they passed through the middle of your cyclotron, you'd engage an alternating electric field to give them a "kick" and accelerate them. As the particles move faster and faster over time, the circle that they make gets larger and larger, as the magnetic field -- a constant quantity -- has a harder time bending the particle into a circle: it's harder to alter a particle's motion when it's got more momentum!
Animation credit: American Institute of Physics, retrieved from aip.org.
In our more modern design, however, we don't use a magnetic field from a permanent magnet and an increasing, spiral path. Instead, we line our particle accelerators — giant rings — with electromagnets, capable of producing just the right amount of magnetic field to keep your fast-moving particle within the ring. This is true whether you’re moving at 99%, 99.99%, 99.9999%, or any other percent of the speed of light, so long as you’ve got your physics right.
Image credit: CERN / Large Hadron Collider.
So the way this works is you inject your particle into the accelerator ring, and tune your electromagnet to just the right level for its speed. Then the particle enters a small region where an electric field can accelerate it — cleverly named an accelerating cavity — which gives it a kick, bumping up its speed by just a little bit. In order to keep the particle moving in the same ring, you’ve got to have the next electromagnet tuned slightly more powerfully, or else this particle will smash into the side of your ring!
Image credit: Madri+d science & society section.
So you ramp your electromagnet’s field strength up each time you accelerate your particles just a little bit more, and as you get progressively closer and closer to the speed of light, you adjust your magnet to keep your particles where they need to be. And whether your particle is moving at 299,492,093 m/s or 299,492,108 m/s makes all the difference in the world as to whether it stays in the ring or slips out, slamming against the side of the accelerator.
Image credit: aerial photo of the Tevatron, retrieved from physis.ro.
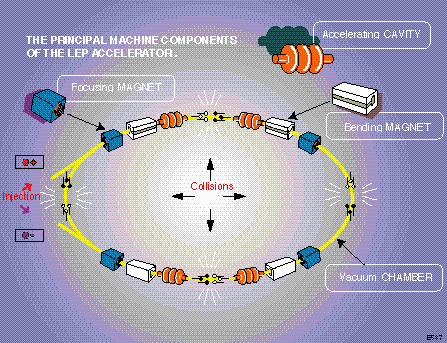
Older accelerators, like the Tevatron (above), accelerated particles in one direction and antiparticles (with the same mass but opposite charge) in the opposite direction. Over the span of thousands and thousands of trips around the ring (with each trip taking just microseconds), they would be accelerated up to their maximum speed, with the electromagnets consistently ramping up towards their maximum field strength to accomodate them!
While the point of the science was to see what interesting things pop into existence when these high-energy particles and antiparticles collide, you needed to carefully calibrate the electromagnets and accelerating cavities to operate at just the right frequencies to account for these particles as they sped up along their way to as close to the speed of light as they could possibly get! In fact, like many undergraduate interns, it was one of my very first jobs (back in 1997; hi, Roger and Erik) to make sure the electromagnets that bent the particle beams at the Tevatron were optimized to achieve the particle energies (and luminosities) we wanted, up to 99.999956% the speed of light!
Image credit: Large Hadron Collider from the air, retrieved from Paul Sanghera.
Today, the energy record is held by the Large Hadron Collider at CERN, with protons achieving individual speeds of 299,792,447 meters per second, just 11 meters per second shy of the speed of light! (Go ahead and calculate it for yourself!) After the LHC’s impending energy upgrade, it’ll get even closer: up to 299,792,455 m/s, or a tantalizing 99.9999991% the speed of light.
Protons don’t move at or faster-than the speed of light; we’d actually be able to tell, from our electromagnetic adjustments of the accelerator, if they were. But they’re not even the fastestparticles we’ve created!
Image credit: LEP accelerator, retrieved from particle.kth.se.
Because even though electrons and positrons at LEP — the Large Electron-Positron Collider that was dismantled to make room for the LHC — only got up to a maximum energy of 104.5 GeV, or just 1/33rd of what the LHC gets, a proton has nearly 2,000 times the mass of an electron! What does this mean for speed?
It means LEP’s electrons and positrons reached maximum speeds of 299,792,457.9964 meters per second, or a whopping 99.9999999988% the speed of light, just millimeters per secondslower than light in a vacuum.
And yet, they were slower than light, and we can tell! So whatever the verdict winds up being with these neutrinos, rest assured that all the protons and electrons that make up you and the world you love are still bound by the laws of special relativity. And that's how we know!
- Log in to post comments
More like this
Thank you for an awesome explanation of what I (used to) do for a living (before I started searching for dark matter).
Back when I was still young and naive, I got sucked into meeting with an Autodynamics nutcase. No matter how I tried to explain that SLAC wouldn't even function if SR was wrong, I just couldn't get it across.
I'm not sure this post would have succeeded either, but it is wonderfully clear on the concept.
Another well thought out and articulate post.
If you assume that both the supernova neutrino and the CERN neutrino measurements are correct, what constraints would that put on the Cerenkov-like radiation from superluminal neutrinos?
ie, the supernova neutrinos started off faster than c, but lost speed thru emissions with a half-life of X.
X would have to be sufficiently long to not see the Cohen-Glashow radiation between emitter and detector, but short enough to bring the speed down to c before the neutrinos could outrace the light by much.
Aha neat! Because of that first part I wondered why it was an integer and guessed that meters must actually be based on speed of light in a vacuum. Wiki confirmed it, yay I learned something neat today. Seems it used to be based on wavelengths of light but has since been changed to the speed.
Maybe that's why us Americans can't deal with the metric system. It keeps changing on ya ;-)
I clearly see the point. You cannot accellerate matter beyond the speed of light, with using electromagnetism as a force.
I use to compare it to a ship in a storm. No matter how big sails you set, the ship will NEVER travel faster than the storm, but you can get very close, probably 99,99999 % of the speed of the storm, if you set a very big sail.
This is logic.
However I still believe that travel beyond the speed of light is possible. We just have to use another force than electromagnetism to get there.
Before finding electromagnetism, we knew nothing about it.
Today we know nothing about possible forces above electromagnetism, but I am pretty sure they will be found, when we start looking.
And we have to start by revising Einstein.
I have a proposal at
http://crestroyertheory.com/the-theory/
I know for sure that some of it might very well be wrong, but we have to start rethinking physics.
We do not find the Higgs boson, that I am pretty certain about.
After that, the standard model collapses, and physicists have to find new theories.
"And that's really exact, 299,792,458.00000000... (etc.) meters-per-second. "
Until the difference between the definition of the second and the definition of the meter and the measure of the speed of light cannot be reconciled and it is decided to change the speed of light.
It may be that one of the other items would get changed, the decision of that depending on what the magnitude and effect of change needed to square this circle would be.
PS how would this work with the uncertainty principle? There's inherent undertainty in location (needed to find when something passes a point), and the momentum (related to either speed or energy of a photon) if by speed, then the velocity at those points measured is uncertain. Something going 299,792,457.0 +/- 1.2 m/s could appear to be going faster than light...
"But we've spent generations trying to accelerate matter as close to the speed of light as we possibly can under extremely controlled laboratory settings"
What was the lightest particle so accelerated under extremely controlled laboratory settings?
@7 Wow
Neutrino ;)
Aye, the problem is neutrinos aren't charged, therefore we can't control them accurately. There's another problem that you can't pigging well find them, so you need lots of them and can't control where they are or go.
And the neutrinos are very much higher energy and very much lower mass than most of the neutrinos I can recall having been detected when I was "in the industry" about 24 years ago and heard of since then.
Mind you, 24 years ago, neutrinos went at the speed of light, so were at that time considered massless.
Saying "you're wrong" isn't good enough. You have to explain why they got it wrong. "Experimental error" may still be valid, but it's not as valid as the first time that was the reasoning.
Getting a good proof as to why they have it wrong leads them to discover how to make it not wrong in that way. And if it really isn't happening, then the FTL neutrinos will be shown to be sublight neutrinos.
If it stands up to the testing, then FTL neutrinos become a theory and we can ask "well, what does it mean?" just like asking "things going near lightspeed gains mass" means we have nuclear power. Or the Lamb shift shows that electrons aren't whizzing round in an orbital, but are to an extent "really" spread around their orbital.
Wouldn't in the experiment you described a faster than predicted particle smash into the wall because the system isn't tuned for it?
If neutrinos just give a small jump thru another dimensions after their creation, and then move under the speed of light, you'll not have any Cohen-Glashow radiation. That would be confirmed if the early arrival time is inversely dependent on the baseline - so far we have 60 ns with OPERA, and nearly zero with 1987A. We can wait for MINOS, and/or plan an experiment with a variable baseline. Can't we just put those detectors over a wheelcart?
[quote]And we know the speed of light in vacuum -- in perfectly, completely empty space[/quote]
The perfectly, completely empty space is in fact full of vacuum energy, as you repeatedly explained.
Could this energy act as a medium? Do photons interact with energy?
This would explain why they travel slightly below c even in "vacuum".
Also, I never understood how photons have no rest-mass if they are effected by gravity? They must instead have a non-zero mass, though too small to be detected.
Can someone explain it to me?
The second illustration shows something else than it was designed to. Because the neutrino beam passes under the mountains (11.4km deep) then the gravity it experiences will be less than that experienced on the surface. This means that time will be a little bit faster than at the surface, too, and thus light would also be faster than at the surface. I haven't checked on the conditions in which that speed-of-light is specified, but I expect it was at 1g rather than in totally free space - it's somewhat difficult to actually measure it elsewhere at the moment. I'll do the calculations sometime, but it seems like a reasonable explanation for a few parts per billion difference.
@5: "No matter how big sails you set, the ship will NEVER travel faster than the storm"
Simplistic analogies are surprisingly often simply wrong.
https://en.wikipedia.org/wiki/Sailing_faster_than_the_wind
@14
This is such a comprehensive pwning I think it may be a [wning.
@12 Pronoein
Agree with you that the sentence isn't correct. Vacuum of space is not perfectly, completely empty. Don't understand why Ethan even stressed it in such a way.
Also am a bit surprised that he never mentions the electric and magnetic constants of vacuum since they play a role in speed of light. i.e. those values weren't what they are, the speed of light would be way different.
As for photon mass, it's very easy to calculate in relativistic terms. Just plug it in E=mc2, then you have m=E/c2. If you know the photon's energy, you know it's mass. The paradox is that if it doesn't move, it doesn't have mass. When I use to study SR in school this always bugged me. It's rather difficult to imagine a photon "coming into existance". I.E a light bulb. The current passes through a wire, and all of a sudden, from nowhere this photon comes to be and in that instant it has speed c. It doesn't accelerate to it.. it just is. Then a while later, it gets absorbed somewhere, and it's speed is now 0, it has no mass, it doesn't exist anymore. How can it go from 0 to c or back without accelerating or decelerating. This is still a thought experiment that I have trouble understanding.
@Sinisa Lazarek (16):
Imagine an empty space with absolutely no change in its potential, lets say all voltage-differences between all points in this space were ZERO.
Now, by whatever source, give exactly one point a non-zero difference - a DIRAC-pulse.
What will happen?
This difference will propagate away from this point, with that speed which is possible for its propagation in the medium. From zero to speedlimit within a near-zero interval of time (one PLANCK-time unit?).
The momentum of the forming wave is sourced from the original DIRAC-pulse - it is transformed to the spreading 3D-sphere-wave.
Does this help?
Cheers.
@17 Schwar_a
Thank you for your replies in this and other topics. Much appreciated :)
There are 2 things which still seem problematic in your "mental image".
1. It is a good way to imagine it if it was only a wave. If I try viewing it as a particle... then it's not so clear.
2. I am unsure (and this is just my opinion) that Planck time is a "quant" of time. Or in other words, am unsure that time has a fundamental building block. The question is a profound one. Does Universe tick in Plank units? I don't believe that it does. It still can stand that a photon will go 0->c in one plank unit. The problem I have is that I don't understand 0->c in material world without acceleration. If time has a quant, yes, but like I said, don't believe that it does. :(
@ 17
p.s. It is indeed a good philosophical question. Are Plank units a real thing (a real end/begining of existance) a sort of a event at which things get their size etc.. Or is just a mathematical/physical tool to cope with infinity.
"1. It is a good way to imagine it if it was only a wave. If I try viewing it as a particle... then it's not so clear."
But the item is neither. It is what it is. We model it as a wave or a particle depending on what we want to look at.
I.e. the photoelectric effect doesn't work if you use the wave model of light, and the double-slit experiment doesn't work if you use the particle model of light.
"2. I am unsure (and this is just my opinion) that Planck time is a "quant" of time."
You can't tell the difference between events smaller than the planck time. You can't measure an interval to any better precision than the planck time.
In so far as measurement is concerned, the plank time is a quanta of time.
Hi Sinisa and Wow (18-20):
I agree, the particle image for a photon, usually seen as a piece of matter, which has mass, does not help here.
(BTW: is the photoelectric effect the ONLY experiment, which NEEDS particles??)
Related to the PLANCK-time:
Imagine you create a wave, let's say with a rope. Now you toggle ever faster and faster.
What happens?
Due to the "resistance", here mainly inertia, at some point the rope will no longer transport running waves away - the reflecting energy gets too large, the "source" produces more energy than is possible to transport away through the current medium.
This point in quantum world is the world of PLANCK-units.
A wave cannot be shorter than the PLANCK-length l_pl or it would be damped more and more. The PLANCK-Time t_pl as the shortest time to move the distance of l_pl is related to that. etc.
Cheers.
@Sinisa
If time can be considered "motion plus memory", then it can (must?) be quantized.
A clock ticks, a pendulum swings, an atom decays - ALL ways of measuring time involve something moving and being able to record that it moved.
We use the same language to describe time and motion too: time 'speeds up' or 'slows down', etc. Freeze-frame a scene: has motion stopped, or time?
We can remember our past, sure, but the Universe can't. It exists only in the present, with no memory.
Talking of which... If you could ask a 14Bn-year old photon from the Hubble Deep Field how old it is and how far it's traveled, it would tell you it's only just left the star it set off from, took no time at all to hit your retina, and wonder why you're asking such stupid questions and pretending your eye is on the other side of a vast and ancient Universe...
As far as the photon is concerned, there is no such thing as time, motion or distance. And from its point-of-view, it's correct.
...perhaps you may also look to the concept of the photon-sphere somewhere.
This concept shows that a wave with λ=2Ï·l_pl is the only wave, which can orbit with radius l_pl conforming to SCHWARZSCHILD and gravity. Smaller wavelengths would be swallowed by the sphere, larger ones can escape and may have effect outside...
Cheers.
(BTW: is the photoelectric effect the ONLY experiment, which NEEDS particles??)
No, though it's the clearest example of its interpretation as a wave being wrong. Note: it doesn't have to be solved by *particles*, just that it can't be solved by *waves*.
Thank you all for the input. Will research more.
Just a few comments.
Yes, yes, about the speed of light being the limit for charged particles. Very nice summary,
For uncharged particles, i.e. neutrinos, I await experiment confirmation (i.e. acceptance by the experts) regarding faster than light neutrinos or not. But could someone clarity, how or why does the weak interation (I assume) eject particle (i.e. these muon neutrinoes) at nearly the speed of light?
For example, do all nuclear interactions eject all particles (e.g. electrons) at near the speed of light; but (maybe) the electrons get slowed by EM force? Can someone help me understand? Thanks.
Last point, regarding plank time.
Planck time is 10^-44 sec
The shortest time interval ever meansured is about 10^-25 sec (e.g. Z particle half-life)
Lot's of people describe Planck time as the shortest physical time interval. I'm not convinced. No, I don't want time intervals smaller; I want them bigger. Maybe the smallest physically meaningful (i.e. measureable) time interval is 10^-25 seconds. I mean if you believe 10^-44 sec is possibly physically meaningful; then you ought to be able to describe some possible physics measurable between 10^-44 sec and 10^-25 seconds. 19 orders of magnitude is just to great a gap for (in my opinion) credible speculation. Unless, you can tell me; here is something that we're trying to measure at 10^-30 seconds and another thing at possibly 10^35 seconds? If theory doesn't point to some such experimental goals; then all we got is Planck time numerology. So, please educate me. Thanks.
OKThen,
(DISCLAIMER: I am not a theoretical physicist, so some of what I'm posting may be corrected by others. However, this is my best understanding of it. Please be nice to me everyone :) )
The Planck time arises from quantum theory and general relativity and is an attempt to determine the shortest theoretically measurable duration. Quantum theory states that DeltaE * Deltat <= hbar, where DeltaE and Deltat are the indeterminancies of the energy of the "clock" used to measure the time interval and that of the measured time interval respectively. Clearly, to be considered a measurable time interval, the indeterminancy of the measurement cannot be larger than the measured value. Equally clearly, if this quantum mechanical relation were all that played into it, the time indeterminancy could be made arbitrarily small by increasing the energy indeterminancy.
However, general relativity also comes into play. One of the results of GR is that the energy of a system of a given size cannot increase without bound; eventually after sufficient energy is concentrated in a region, a black hole will form. The combination of the condition that the time indeterminancy must be no greater than the measured time and the condition that the energy indeterminancy must be no greater than the energy needed to form a black hole results in the formula given for the Planck time.
Just to give a more concrete example, it would be possible to measure a time by passing light from a source to a detector, assuming that the distance between the source and the detector is known. Theoretically, to measure the distance, we must scatter a wave from it. For an ordinary distance measurement, we use a ruler, but we must also use light to read the ruler. The accuracy with which we can read the ruler is limited by the wavelength of the light used to read it. Shorter wavelengths are needed to more accurately measure the distance.
Quantum mechanics tells us, however, that the wavelength of light is inversely proportional to the energy of the light. If we decrease the wavelength to get a more accurate measurement of the distance, we increase its energy. It's possible to increase the energy of the light to the point where pair production occurs, mass accumulates and a black hole forms. This is the theoretical best precision with which a distance can be measured. The measured time is then the speed of light divided by the distance. If the measured distance is this theoretically most precisely measurable distance, we get the Planck time as a result. (Of course, you probably figured out that the "most precisely measurable distance" is also the Planck length.)
Wouldn't a neutrino detector have to be already pointing at the star that was about to go supernova in order to be able to check that the light AND the neutrinos arrived at the same time?
If we saw the star visually go supernovae and THEN point our neutrino detectors at it then surely we wouldn't be able to say that they go the same speed?
Sure. Furthermore, there is no reasonable way to provide the field transformation for a charge moving faster than c. Consider just uniform motion. The E field is weakened to gamma^-2 in the direction of motion, but increased to gamma times more lateral to motion (field lines Lorentz contract just like they were radial wires from the charge, with the expected implications for field intensity.) Also the lateral magnetic field B is proportional to gamma*v. So, both those quantities become absurd even at c, much less beyond it, and surely other things go wrong.
Note however, that effective gamma might be based on a "true" limiting velocity, that light only approaches (due to maybe syrupy effects of quantized space etc., yet note e.g. that the Planck-scale foaming was essentially ruled out because it doesn't scatter ultra-high-energy gamma rays.)
BTW, those and other features of fields show that forces between particles are not always equal and opposite as Newton supposed (good and practically accurate guess though given what he knew and had reason to believe.)
"Fine minds make fine distinctions."
@27 Sean
I appreciate the effort; but it doesn't answer my question.
If you are going to use light to measure the time then you need a source of light with a rapid enough frequency. Gamma rays have a frequency of 10^19. So you can use a single gamma wavelength to make a time measurement of 10^-19 seconds.
So I need much more energetic photons than gamma rays to measure time intervals smaller than 10^-19 seconds with photons. So what do I use? Well not photons. I do not know how some excellent scientists determined that Z and W particles have half lives of 10^-25 seconds. Nice work though and I'm sure it involves physical insight and statisitics.
So what physical insight gets us to look for a physical process with maybe a time interval of 10^-30 seconds? I don't know. That's what I'm asking. I don't know. So talking about 10^-44 is nice but what physical process can we use to measure (observe) such physical events?
@OKThen (30):
Since the shortest decaytime ever measured is that of the top quark with about 5·10^-25 s, this seems to be the shortest interval of time we can reasonably use at all for time-measurements in the macro world.
Shorter times make no sense, due to HEISENBERG's Ît·ÎEâ¤h/(4Ï)...
To my opinion, there _is_ a big gap downto PLANCK-time, but this obviously doesn't matter...
"How" this time-measurement, especially that of the top quark decay, is actually performed, is also interesting to me. It could never been directly, I guess...
Does anybody know something about this subject?
Cheers.
The problem is that you are assuming that the theoretical maximum frequency of a gamma photon is equivalent to the highest frequency gamma photons that we have actually produced. There's really no reason to believe that this is the case. However, there is a theoretical maximum for the frequency of a gamma photon. The gamma photon has an energy equal to the Planck constant times the frequency, ie E=hf. If the frequency becomes high enough, the gamma photon will yield an antimatter-matter particle pair. If it becomes REALLY high, it will produce enough mass to collapse itself into a black hole. The frequency at which the gamma photon acquires sufficient energy to do this is the maximum theoretical frequency. The inverse of this frequency would then be the shortest possible time interval, which of course is the Planck time. The fact that we haven't observed this "maximal frequency" photon to date is not evidence for its nonexistence. It's merely evidence that we haven't been able to produce a sufficiently energetic process to yield it.
SCHWAR_A,
My understanding is that the Planck time has nothing to do with any measurements that we have actually performed. I have no idea whether top quark decay could be used as a method for measuring short time intervals. It's irrelevant to the matter, however. To measure ever shorter time intervals requires increasing energies. The lifetime of the top quark is an example of this; it takes a lot of energy to produce top quarks in the first place. My post above gives another example. The inverse of a photon's frequency would yield a short duration. The higher the frequency, the shorter the duration. However, higher frequencies mean higher energies. There is a limit to the amount of energy that can be concentrated in a given volume of space. This limit on energy concentration also places a limit on how short a time interval can be measured. That's where the Planck time comes in. It's the THEORETICAL minimum time duration that can be measured. The fact that we haven't found a physical process that actually yields a time duration at the Planck scale is simply evidence that we have yet to produce enough energy to reach the Planck scale.
Only if there's something to take care of the momentum problem, Sean.
Pair production happens near another mass.
Last I heard, anyway.
The problem being having a vacuum enough to stop pair production taking place.
"Theoretically, to measure the distance, we must scatter a wave from it. For an ordinary distance measurement, we use a ruler, but we must also use light to read the ruler."
Though you can use a ruler (with mm or 1/32nd" markings) to measure the wavelength of visible light.
So you can get a little bit more resolution if you set things up right.
Wow,
Like I said in my disclaimer, I'm not a theoretical physicist, so I'll defer to you. I was just trying to provide a more or less simplistic explanation, to the best of my own knowledge, of why there's a theoretical minimum time that can be measured.
Neither am I, Sean.
But I do remember that I was shown (and can no longer remember) proof that pair production needs a nearby mass.
It may be that that problem can be sorted by a different method with the advances in field theory.
Sean Tremba, a photon can't ever have simply "so much mass-energy it will collapse into a black hole" - remember, the energy of a photon is relative to a reference frame. So in which frame would it have that energy? If someone was approaching a petty visible light photon fast enough, that photon "has" enough energy in that frame to become a BH if that theory was valid, etc. And yes, pair production needs a mass, it can't happen to a photon spontaneously! (No "proper duration" for photon, to have chance, etc.)
@Neil Bates:
thank you for this clarification.
Related to the maximum energy we are able to produce:
Since we need higher energy to measure lower energies, isn' t there an upper limit given by the highest particle energy, namely that of the top quark? So I think, its lifetime is the shortest we can actually use.
Cheers.
SHWAR, the "lifetime" of a particle is the half-life, since it decays by random process.
Therefore some times it will decay shorter than the half-life.
A tick shorter than the minimum you would ascribe to our smallest usable time period.
Therefore not actually the minimum we can use.
If we could see a difference between the decay time spectra as a continuous time function and the decay time spectra as a quantised time function, then we could consider the time decay as some near-minimum we can usefully ascribe to an event.
At the moment, we can't detect any time quantisation, so we can go a lot shorter.
@Wow:
Thanks.
Do you know, how such times actually are measured, since atom clocks have a much less resolution?
Atomic clocks have a much better resolution (at least in theory). They use a metastable decay that lasts a long time but (due to the fact you have reduced variation) great accuracy. You'd then divvy that up to the small times.
I was never that much into elementary particle physics (the professor lecturing on it was FAR TOO SMART to teach it).
But you can see the half life still with enough examples and just waiting for several half-lifes, then work back to what half-life gives you that fractional reduction.
Because it's stochastic, you get large errors this method, so I suspect they use different methods.
As far as the theory goes, the depth of the energy well (the binding energy or energy state between a particle and its decay product) tells you how quickly a particle will decay.
The heavier a particle is, the quicker it will decay (if there is a decay product to go to). The bigger the difference between the particle and its decay products mass, the quicker they decay.
The top quark decay is faster than any possible clock at the moment (in theory we could manage ~10 picoseconds) so it's currently estimated by this method.
I note that it appears like I'm saying we can see a few decay times of the top quark, this wasn't my intent. My intent was we can detect deviations from continuous and discrete at orders of magnitude higher resolution than the decay period.
And a short decay product would be a terrible natural tick, since (Heisenberg again) there is a lot of jitter in that short period.