"There are three hundred and sixty-four days when you might get un-birthday presents, and only one for birthday presents, you know." -Lewis Carroll
It's the end of the week once again, and so it's time for yet another Ask Ethan column! This week, I was asked a wonderful math question by Keith H., who wanted to know:
Among my 1,434 [Facebook] friends, it's nobody's birthday today. Given the 365.25 days in a year, what are the odds of a day like this? Show your work.
Assuming that none of your friends were born prior to March 1, 1900, this is the right starting point.
Image credit: ePrint Calendar, via http://eprintcalendar.com/.
In the last 114 years, there has been a leap year every four years. If you assume that everyone you know was born at a completely random date-and-year in that timeframe (a generally good enough assumption), there's a 4-out-of-1461 chance they were born on any given date except for February 29th, and a 1-out-of-1461 chance that they were, in fact, born on February 29th.
Assuming you had any number of friends, what are the odds that no one would have a birthday on today's date?
Let's start with one person.
Image credit: IGN forum member Gameovertime222.
Assuming you have just one friend and that today is a non-leap day, the odds that this friend of yours will not have a birthday today is 1457-out-of-1461, or 99.73%. The nice thing is, this is true for every single friend you have, independently.
So the second friend has a 99.73% chance of not having today be their birthday, the third friend has a 99.73% chance of today not being their birthday, the 100th friend has a 99.73% of today not being their birthday, and so on. Let's say you have six friends, to keep things simple: what are the odds that no one's birthday is today?
Image credit: me.
It's 98.37%, because you need the first person to not have their birthday today and the second person to not have their birthday today and ... and so on. If anyone has their birthday today, the game is ruined.
The fun thing is, you can extend this for an arbitrary number of people! Here are some fun stats.
| Number of Friends | Each one's unbirthday odds | Total unbirthday odds | Expressed in percent |
|---|---|---|---|
| 1 friend | 0.99726215 | (0.99726215)^1 | 99.73% |
| 2 friends | 0.99726215 | (0.99726215)^2 | 99.45% |
| 5 friends | 0.99726215 | (0.99726215)^5 | 98.64% |
| 10 friends | 0.99726215 | (0.99726215)^10 | 97.30% |
| 50 friends | 0.99726215 | (0.99726215)^50 | 87.19% |
| 150 friends | 0.99726215 | (0.99726215)^150 | 66.28% |
| 253 friends | 0.99726215 | (0.99726215)^253 | 49.98% |
| 365 friends | 0.99726215 | (0.99726215)^365 | 36.76% |
| 500 friends | 0.99726215 | (0.99726215)^500 | 25.39% |
| 1000 friends | 0.99726215 | (0.99726215)^1000 | 6.447% |
| 1434 friends | 0.99726215 | (0.99726215)^1434 | 1.961% |
| 1680 friends | 0.99726215 | (0.99726215)^1680 | 0.9993% |
| 2000 friends | 0.99726215 | (0.99726215)^2000 | 0.4156% |
| 2500 friends | 0.99726215 | (0.99726215)^2500 | 0.1055% |
| 3000 friends | 0.99726215 | (0.99726215)^3000 | 0.02679% |
| 5000 friends | 0.99726215 | (0.99726215)^5000 | 0.0001113% |
(The caret symbol -- ^ -- denotes an exponential.)
As you can see, if you have only a few friends, there are very good odds that on any particular day, no one will have a birthday. But those odds drop down to 50-50 at the 253 friend mark, and decrease rapidly from there. By time you get up to Keith's number of 1434 friends, you've got less than a 2% chance of no one having a birthday today; those odds drop below 1% at 1680, and by time you get to Facebook's limit -- 5000 friends -- there's only a 0.0001113% chance of having friends without a birthday today, or about 1-in-900,000.
But what if we wanted to go more general? What if we wanted to know what the odds are of having at least one day in the year where no one has a birthday?
That's a lot harder.
Image credit: pirata3 of deviantART, via http://pirata3.deviantart.com/art/Happy-no-Birthday-159956821.
You see, whatever the odds are that no one has a birthday today, you subtract that from 100% to get the odds that someone has a birthday today. In order to have at least one day where no one has a birthday, you can subtract the odds that someone has a birthday on every single day from 100%. (Obviously, this is only possible if you have at least 365 friends!)
Here's what the odds of that look like.
| Number of Friends | Daily unbirthday odds | Daily birthday odds | Odds of birthday every day | Subtracted from 100% |
|---|---|---|---|---|
| 365 friends | 36.76% | 63.24% | (0.6324)^365 | 100% - 2.3 × 10^-71% |
| 500 friends | 25.39% | 74.51% | (0.7451)^365 | 100% - 2.3 × 10^-45% |
| 1000 friends | 6.447% | 93.553% | (0.93553)^365 | 99.9999999973% |
| 1434 friends | 1.961% | 98.039% | (0.98039)^365 | 99.927% |
| 1680 friends | 0.9993% | 99.0007% | (0.990007)^365 | 99.927% |
| 2000 friends | 0.4156% | 99.5834% | (0.995834)^365 | 97.44% |
| 2500 friends | 0.1055% | 99.8945% | (0.998945)^365 | 31.97% |
| 3000 friends | 0.02679% | 99.97321% | (0.9997321)^365 | 9.32% |
| 5000 friends | 0.0001113% | 99.9998887% | (0.999998887)^365 | 0.0406% |
And there you have it: if you have fewer than about 2000 friends, there's a near certainty that there will be at least one day where none of your friends has a birthday, and yet if you have more than about 4000, there's virtually no chance that you'll have such a day! Food for thought -- and a little math fun -- for this week's Ask Ethan.
And now that we've reached the end of another Ask Ethan column, it's time for me to flip the script and ask you a question! I know that a great many of you are continuing to enjoy all the great Starts With A Bang content on our new home on Medium, but I also know that most of you are dissatisfied with the options for commenting there.
So I thought I'd throw out an idea and see what you thought: what if I began posting here the introduction to each new post with a link to the full text -- something like this Tumblr website I set up -- where each post would look something like this:
Image credit: screenshot from http://startswithabang.tumblr.com; original article here: https://medium.com/starts-with-a-bang/ef36f2bb2ad1.
Then we could have open comments here -- and I can still moderate, etc. -- so all of you could still have your say both to me and with one another. The Medium gig is too beneficial for me in a myriad of ways to stop doing it, but the one thing I miss the most is your participation. What do you think of this idea? I thought I'd put together a poll for your feedback, if you'd like to participate.
Feel free to comment below if you have suggestions, and I hope you enjoyed today's Ask Ethan. Don't forget to leave your questions and suggestions here!
- Log in to post comments
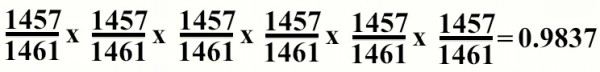
Keith H may sport more awesome facial hair than even you! Grat Column, as usual.
I'm pretty sure your approach to calculating whether at least one friend has a birthday every day of the year is flawed.
Imagine there are only 10 days in a year. For convenience, I'll number them 0-9. Also imagine that I have 10 friends. I can represent their birthdays as a 10 digit number, where each digit represents the birthday of one friend. E.g. 0,058,239,571 means the first two friends were both born on day 0, the next was born on day 5, and so on. From that, it seems clear that there are 10^10 possible arrangements of 10 birthdays in a 10-day year.
Now, the times where there are no birthday-free days correspond to 10 digit numbers containing all 10 digits (0-9). In other words, every friend has to have a different birthday. The number of those should be 10!, since the first friend's bday can be on any day (10 possibilities), but the next has to be different from the first (9 possibilities), and so on. That's 3,628,800 possibilities.
So, if my approach is correct, the chance of a birthday every day of the year is:
3,628,800/(10^10) = 0.00036288
Your approach gives a much different number:
Number of friends = 10
Each one's un-bday odds = 0.9
Daily un-bday odds = (0.9)^10 = 0.3486784401
Daily bday odds = 1 - 0.3486784401 = 0.6513215599
Odds of bday every day = (0.6513215599)^10 = 0.0137...
So the first calculation says the odds of a bday every day for 10 friends in a 10-day year are ~ 0.036%, while the second says they are ~ 1.4%. At least one of those must be wrong.
The other reason I think your approach is flawed is that it will give a positive probability of a bday every day even if you have fewer friends than there are days in the year. But, as you noted already, that can't be true.
Unfortunately, I don't know how to correctly calculate the chances of having an un-bday in a normal year with any arbitrary number of friends. I suspect the problem in your approach lies in treating probabilities as if they were independent when they actually aren't, but I'm not sure.
No, Ethan's right, but there's a simpler illustration. Using a die for the example: the likelihood to tossing a 4 in a single toss is 1/6. The likelihood of not rolling a 4 is 1-1/6. The likelihood of not rolling a 4 in, say, 8 tosses is then (1-1/6)^8. Now simply replace 1/6 with 1/365 and ^8 with ^number of friends and you get Ethan's values.
Yes, I agree that gives the correct odds of no one having a birthday on any single day. It's the next part that I think is wrong - calculating the odds that no one has a birthday on at least one day in the whole year.
Again, if you use Ethan's approach with only 354 friends, you get a non-zero chance of there being a birthday on every day of the year. Yet that's clearly impossible when there are fewer friends than there are days.
So I'm still pretty convinced that something's wrong, even if I can't give what I think would be the correct calculation.
I'm also not sure the calculation on the probabilities of there being at least one birthday-free day is correct.
Ignoring leap years, what is the probability that with x people none of them share a birthday?
Obviously, with one person the probabiliy is 1 (365/365).
Adding a second person, there are 364 available days, and only 1 day having a birthday, so the probability that two people do not share a bithday is 365/365*364/365, or about .9973. For the third person there are 363 available birthday-free days, and 2 different birthdays, or 365/365 * 364/356 * 363/356, or about .9918. And so on. If I did the math right (i.e., wrote the program right), when I get to 365 people, the probability none share a birthday is about 1.4550e-157.
I also wrote a little program to randomly assign birthdays to 2000 different people, and then check if there is at least one day without a birthday. Doing this 10,000 times, 7,248 (72.48%) times there was at least one birthday-free day. Even taking into account the randomness of the process, this is far enough from the number above (97.44%) to suggest the number above may not be correct. (if someone else wants to check my results...)
Rick, I also wrote a quick code, and I think you are answering a different question than Ethan is. His original question was what are the chances of none of your friends having a birthday *today*. Your question is whether any day in the year exists without birthdays. It would seem that those two probabilities are related, but significantly different. It may be that they are related by a factor of 1/365, but I am not sure.
Steven,
The OP asks both questions. Just below the calendar graphic, there's this:
But then, just above the "Happy No Birthday" graphic, there's this
It's the analysis below that part that Rick and I are disputing.
Steven, as qetzal points out, the post asks two related questions, the first is the probability of a person having a birthday today, and then generalizes the question to "What if we wanted to know what the odds are of having at least one day in the year where no one has a birthday?". It's the answer to the second that seems to be incorrect.
I think the problem may be that the approach used assumes statistical independence of the probability of the number of birthdays on each day, when they are not actually independent. For instance, if we have 2,000 friends and today has no birthdays, then all the 2,000 birthdays need to be distributed over 364 rather than 356 days, while if today has 10 birthdays, then the other 364 days will have only 1990 birthdays distributed over them. Thus the number of birthdays today affects the probability of birthdays falling on every other day.
Ignoring leap years, so every years has 365 days, we can analyze the problem like this:
Suppose after X birthdays have been randomly chosen, the probability of their being n days without birthdays is p[n]. Now, if another birthdays is added, then if they birthday falls on a day that another birthday already falls on, then the number of birthday-free days does not change. SInce there are n birthday-free days, the probability of this number not changing is (365-n)/365, which is the probability of a birthday falling on a day which already has a birthday.
On the other hand, if the newly added birthday happens to fall on a previously birthday-free day, with has a probability of n/365, then the number of birthday-free days goes down by one.
So if the probability of there being n birthday-free days after X birthdays, then after X+1 birthdays the probability of their being
n birthday-free days is the probability that there were n birthday-free days before times the probability that the new birthday falls on an already taken day, plus the probability that there were n+1 birthday-free days previously times the probability that the new birthday falls on a previously untaken day. Or, if the probability there are n free days in p[n] before,, then the probability after is (365-n)/365*p[n] + (n+1)/365*p[n+1].
I wrote a program which iterates through this for all possibilities of 365 free days (before any birthdays have been added) to 0 free days. Within the limits of precision of the floating point numbers, I get the following:
1000 birthdays the probability of there being at least one birthday-free day is ~1. 2000 gives .727, which agrees with my previous random estimate of .7248. 2500 gives .271, and 3000 gives .074. For 4000 birthdays, .005.
There is indeed a problem with the "at least one person has a birthday every single day" approach. Ethan's approach would work in a slightly different situation: namely if we were taking random samples from an infinite population of people. If we took a random sample then checked for the first of Jan, then took a second sample and checked for the second of Jan, etc. all the way to the end of the year, the chance that we would get a birthday on every single day of the year would be Ethan's exact values.
However this is different from the question posed. The problem is that within a single sample (i.e. the facebook friends) the probabilities are conditional: the chance of having a birthday in the sample on the first on Jan affects the probability for the second of Jan.
The problem with this method can be shown with the example of a year with 2 days and 2 people. Here, the chance of having a birthday on each of the two days is quite obviously 1/2. Using the method above however, the calculation is (1-(1/2)^2)^2 = 9/16
Can someone please calculate this compound probability question for me? Whatis the probabiiity of five our 25 people having birthdays in November? Thanks!
Did you seriously just use someone's creepy foot fetish deviant-art as a visual aid here? Don't you realize the person who drew it did so for masturbation purposes?