Comments of the Week #17: From solstice to subatomic and smaller

"We converse as we live by repeating, by combining and recombining a few elements over and over again just as nature does when of elementary particles it builds a world." -William H. Gass

Only here, when you repeat, combine and recombine your letters and words, the thoughts, questions and comments you submit are as completely as though no one else in the world had the same ones you did. This past week over on the main Starts With A Bang blog saw us take a deep dive into a number of diverse topics, including:

• Is the Sun brighter in the summer? (for Ask Ethan),
• 5 doses of Terry Crews' awesomeness (for our Weekend Diversion),
• The Dumbbell Nebula, M27 (for Messier Monday),
• The Smallest Black Hole in the Universe, and
• The cosmic chronicle of carbon-14 (for Throwback Thursday).

As always, we've set up synopses here on Scienceblogs for you to weigh in and discuss in our forum, and now at the end of the week, I get to respond in long-form to my favorite Comments of the Week! Let's see what you had to say.

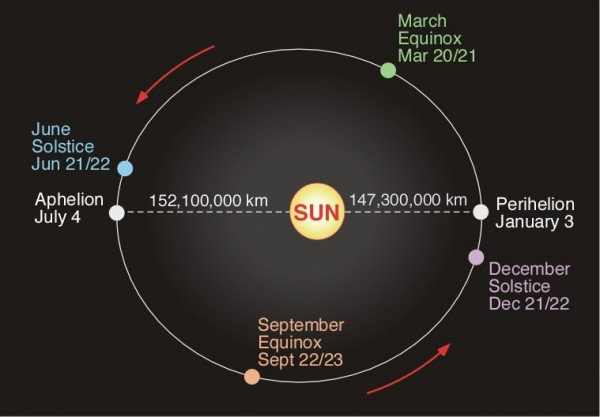Image credit: © 1999-2014 Michael Pidwirny, of Physical Geography at http://www.physicalgeography.net/fundamentals/6h.html.

From Omega Centauri on the topic of the solstices/perihelion alignment of our orbits: "If you go beyond the level of casual observations of apparent strength/heat, the variation of distance is important to the climate. A six percent variation translates into approximately 80watts/ per meters squared, the “forcing” due to human added greenhouse gases is roughly one and a half watts per square meter!"

This is true, of course, in terms of absolute energy. However, it's very important to remember that the difference in angular alignment for someone (like me) at 45° latitude between the solstices translates to a difference of 150% between summer solstice and winter solstice. Even if you gave an extra 40 W/m^2 at the winter solstice and a deficiency of 40 W/m^2 at the summer solstice, you'd still see a summer solstice peak of 1233 W/m^2 and a winter solstice maximum of only 518 W/m^2.

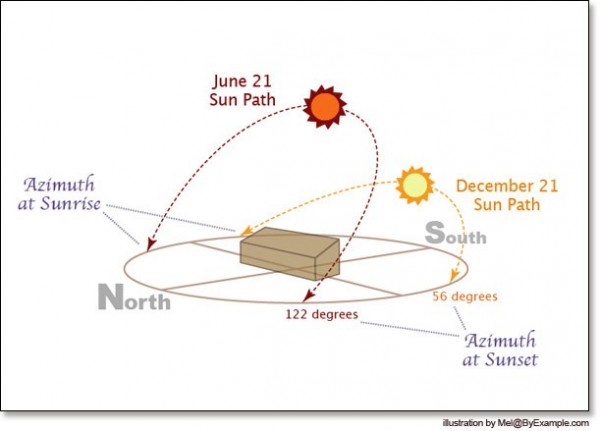Image credit: Mel of By Example, retrieved from Tad at http://bloomingrock.com/2010/04/06/the-single-most-important-energy-sav….

Yes, it's true that if it were the other way -- as it may be close enough to consider to be true for the southern hemisphere -- you'd be talking about a summer peak of 1307 W/m^2 and a winter lowest maximum of just 488 W/m^2. But that's only a 6% shift compared to the 150% shift between summer and winter. The difference between a "short" and "long" season in terms of time, which is less than a week over a six month span, is also a very minor effect. Although it's an unrelated topic, the extra greenhouse gas effects on the climate, which correspond to 1.5 W/m^2 (I'm taking your word for it), is approximately equivalent to either a permanent increase in solar luminosity of about 0.11% or a total decrease in the average Earth-Sun distance of around 100,000 km. The problem with that effect is that it doesn't average out or go away; it just makes things slightly warmer overall for everyone.

Image credit: György Soponyai of Budapest, Hungary, via http://spaceweathergallery.com/indiv_upload.php?upload_id=92546.

From Blaise Pascal on last week's comments of the week about our analemma: "The knowledge of the analemma (and the equation of time it represents) is ancient. Ptolomy wrote of it, and included deferents in his astronomical model to account for it. But I’ve never heard *how* they knew of it. Without mechanical clocks, how did they know about the difference between solar and mean time?"

I don't know how Ptolemy (or others) actually did it, but I know how I would if I didn't have a mechanical clock! All you need, believe it or not, is a primitive sundial, or a stick in the ground with a well-defined edge/top. As the days go by, you'll clearly be able to identify when solar noon is, or when the shadow cast by the sundial is at its shortest. And what you'll find, if you measure that point day-after-day, every day, is that the location of the "shortest" point changes in the same shape as the analemma!

Image credit: MYP students, via http://mypinteract.wordpress.com/category/chapter-6-location-location-l….

All you need to do is measure positions from one fixed location very carefully, with no need to keep track of time. It would become evident that not only did the angle change over time (as the Sun's position relative to the zenith changed with the seasons), but that the "time" of shortest angle appeared to move slow-and-fast as the equation of time dictates. In short, you'd get the same analemma shape you're used to!

In addition, if you could keep track of time, you'd be able to measure all sorts of analemmas using this method -- although they would get stretched as shadows tend to do -- at any time you wanted.

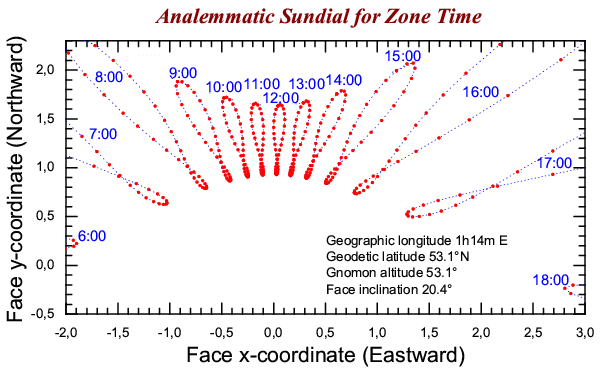Image credit: KM Borkowski of the
Torun Centre for Astronomy (TCfA), NCU, Torun, Poland, via http://www.astro.uni.torun.pl/~kb/Reports/Sundial/Sundial.htm.

So that's not necessarily the answer of how the ancients did it, but that's how I would do it if I only had access to the primitive tools that the ancients did. Fun stuff!

Image credit: Dana Berry/NASA, of a neutron star (L) and a black hole (R), via http://www.nasa.gov/mission_pages/swift/bursts/short_burst_oct5.html.

From Pavel on the smallest black hole in the Universe: "I think we have to wait for the small black holes a bit longer then the 10^68 years. It’s because the black holes are eating the [interstellar] matter and the mass loss caused by the Hawking radiation is compensated by eating 1 proton in 1 trillion years (if I’ve calculated it well for black hole of mass of about 3 sun masses). How long it would take till the Universe will be so empty, that a black hole doesn’t meet single proton in trillion of years?"

You know, one of the nicest things about Hawking radiation and black hole decay is how strongly dependent the rate is on mass. If you take a look at the formula for black hole evaporation time, this is what you get:

Image credit: Wikipedia page on Hawking Radiation, via http://en.wikipedia.org/wiki/Hawking_radiation.

For a black hole of precisely 3 solar masses, that's a time of 5.664 × 10⁶⁸ years. But what if we vary this? If we wanted to get that time down to just 1.0 × 10⁶⁸ years, we'd need to go down to 1.683 solar masses; if we wanted to hit 1.0 × 10⁶⁹ years, we'd have to rise all the way up to 3.626 solar masses. And eating little bits of interstellar matter isn't going to get you there, at least, not quickly enough.

Image credit: NASA/ESA Hubble Space Telescope collaboration.

You see, our Universe, on black hole evaporation timescales, is still in its supreme infancy, with an age of only around 1.38 × 10¹⁰ years. The CMB will soon, like on timescale of around 10¹² years, drop to energies low enough that black hole absorption of that energy will drop below Hawking radiation levels. We may get plenty of new stars and stellar mergers for the next 10¹⁴ years or so, but by time we start approaching 10²⁰ years, most masses -- including black holes -- will get ejected from the galaxy and will simply be hurtling through empty (yes, really empty, thanks to dark energy) space.

Considering that 10²⁰ years is tiny compared to timescales of 10⁶⁸ years, our approximations here are actually very good!

Illustration credit: NASA/CXC/M.Weiss, via http://chandra.harvard.edu/photo/2012/igr/.

Here's one from exclamation point hater Pa Deuce: "Will you knock off the stupid exclamation points? It is terribly distracting."

Let's see here. In a field -- the hard, physical sciences -- famous for droll, monotone communicators, you want me to stop using the, what, three tools I have to emphasize cadence, volume and excitement? So don't use italics, bold, or exclamation points, I suppose, is what you'd want.

You're always welcome to ask, and I'm always happy to make a note of what your feedback is. But we're talking about the most fundamental physical truths of existence here, and even though I do my best to take myself out of it, I don't really want to take my excitement out of it. But to acquiesce a little bit, I'll make it through the entire response to your comment without using one.

Image credit: University of New Hampshire.

And finally, one more from Omega Centauri on the topic of carbon-14: "Obviously that reversion to normal is orders of magnitude too fast to be the radioactive decay of the C-14. The atmospheric CO2 (at least the C atoms), must be being exchanged with a largish reservoir of older carbon -presumably plants, soil carbon, and CO2 dissolved in seawater. On a longer term carbonates in the rocks….. Has anyone been able to use the C-14 ratio as a function of depth in the ocean to estimate how quickly ocean water overturn?"

This is a tough proposition. You have to recognize that when we talk about one-in-a-trillion carbon atoms being Carbon-14, we're talking about atmospheric carbon. Yes, it's true that there is a carbon cycle, where atmospheric carbon goes into the ocean, gets locked up in organisms and rocks and heads underground where it's deeply buried, etc. But it's only the atmospheric carbon that gets rapidly cycled into things like terrestrial organisms and low-depth marine waters and life. As we can tell from these tree-rings, 30-odd years, give-or-take, is about as long as it takes for all the atmospheric carbon to be cycled.

Image credit: Fusa Miyake, Kentaro Nagaya, Kimiaki Masuda & Toshio Nakamura, 2012.

But so far, the only way we have readings of this is through tree rings, where the carbon count is easy to identify. Could we maybe do something analogous to this by dissecting and dating various portions of coral reefs? (Their structures are mostly made of calcium carbonate.) Possibly, although I don't know enough about the biology of these organisms to know how reliable that would be.

The big, problematic issue with this is that Carbon-14 is about one trillionth of the Carbon in our atmosphere, and our atmosphere is only about 400 ppm carbon compounds, and the ocean is about 300 times as massive (with roughly thrice the carbon fraction) as the atmosphere. I'm not saying we couldn't measure this, but I am sure that I don't know how we would, and also that there are other difficult barriers -- such as dilution and background contamination from other, natural radioactive sources -- that might make searching for increased traces of C-14 more difficult at appreciable ocean depths. It's a good idea, but I can't speak positively about the potential practicality of it.

And that will take us to the end of this edition of Comments of the Week! Don't forget to leave yours for a chance at having them answered right here, and I'll see you back here tomorrow (or whenever you come back) for more stories about the Universe, and our place in it!