“I’ve done the calculation and your chances of winning the lottery are identical whether you play or not.” -Fran Lebowitz
It's a thought that's occurred to almost everyone at some point or another: what each of us would do if we happened to hit the lottery Jackpot. Have a listen to Camper Van Beethoven sing about it in the band's interesting song,
while you consider the following.
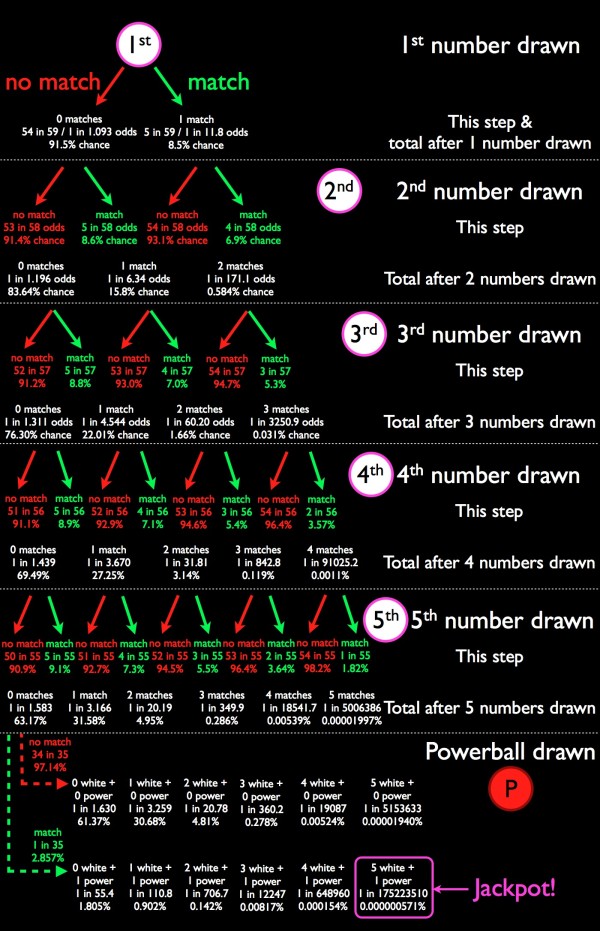 Image credit: me. The (very small) differences in these odds and the Powerball official odds are due to rounding.
Image credit: me. The (very small) differences in these odds and the Powerball official odds are due to rounding.
This past week, the Powerball Jackpot crested past $500 million, one of the largest Jackpots in lottery history. You might think -- since the odds of hitting the Jackpot are "only" 1-in-175,223,510 -- that it's a no-brainer to buy a $2 ticket and take your shot at $500 million. But if you take everything into account, what is the expected value of a Powerball ticket?
 Image credit: screenshot from the official Powerball site, at http://www.powerball.com/powerball/pb_prizes.asp.
Image credit: screenshot from the official Powerball site, at http://www.powerball.com/powerball/pb_prizes.asp.
As it turns out, it's not only less than you probably think, it's much less than you ever imagined. It's often been said that the lottery is a tax on the mathematically challenged, and now you've got the hard, mathematical evidence to back it up!

Someone called it a tax on fools!
Unfortunately it is the poorest people who buy the most tickets.
At least in the UK there is no tax on your winnings until you put it into a bank!
UK has no taxes.
Also there are "rolldowns"
There exist smart investers that win at lotteries.
https://www.schneier.com/blog/archives/2011/08/hacking_lotteri.html
From the article:
If you select your numbers, I'm betting (heh) you can probably significantly reduce the odds that of sharing your prize. First, take most of your numbers above 30 so that you don't overlap with people who pick dates. Second, select 3-4 numbers in a row (example: 41, 42, 43, 44). Most people won't do that for psychological reasons, so you've just produced a ticket which has less of a chance of being duplicated.
Its still a bad bet, but hey, if you're going to do it, might as well try and squeeze the best odds you can out of it.
"If you select your numbers, I’m betting (heh) you can probably significantly reduce the odds that of sharing your prize."
Also by picking numbers near the extremes - lowest and highest possible, since most people, when they choose "randomly", select values in the center of the range.
If played properly, Powerball is like going to the movies: You enter into a fiction for a while and play a harmless game of "what if." When you cannot hold that "what if' loosely, and become deflated by not winning, you know you should not play.
All the math is in keeping with the spirit of this blog, but a lot of people who play aren't really buying a chance to win a few hundred million dollar. They are buying a fantasy. For $2 dollars, you get to say, "When I win the lottery ..." do a little daydreaming.
I must have missed the part where you do the arithmetic and tell us the expected value. But if I remember my economics theory correctly, the expected value of a $2 bet with a jackpot of $5 million is $5.60. So in this particular case, its a 'fair bet' and since your expected value is positive, you should bet.
i don't think betting $2 for the fun of it is dangerous or stupid. It can give you some fun daydreaming so it's worth it. I knew the odds of winning are impossible but it's worth $2 to me for the fun. What I would like this author to do is show the stupidity of buying multiple lottery tickets. I see so many people, without much money, spend a fortune on lottery tickets because they think their odds are better when they buy $50 worth of tickets for one drawing. I know that it has almost no impact. They think it significantly increases their odds. They think if they buy 2 tickets it moves it from 1 in a million to 1 in 500,000, 4 tickets now moved their odds down to 1 in 250,000. If they buy 100 tickets their odds improved to 1 in 10000. Can you show them the real odds and encourage people that if they buy more then 1 ticket that it really makes no difference and is an even bigger waste of money.
@7: you must've just read the synopsis and not the full article; the math you're asking for is in the full article, and th expected value is much less than $5.60.
Note also that lotteries occasionally tweak their systems (I think my local MegaMillions just increased the numbers it draws from one or two years ago). So the chances are very good that some notional lottery system you read about in an economics book does not reflect the way Powerball today actually works.
If they think that, they think correctly. If you bought 175,223,510 different Powerball tickets, your chance of winning would be 100%. Your chance of profiting from the venture would still not be 100%, of course.
IIRC there was an interesting case in Australia where the payout exceeded the odds to such a degree that a consortium of people decided to try and buy one of every possible ticket in order to guarantee they won. The problem is, you can't just plunk down a large amount of money to the lottery commission and get them to agree you bought one of each 'in theory,' you have to physically buy all those tickets. And then you have to find that winning ticket in your inventory to claim your prize. It became a race as to whether the consortium could actually, physically accomplish all the purchases before the draw time arrived. IIRC they didn't but they did get to credible odds (I want to say about 33% chance of winning, but my memory is hazy). If I can find the story, I'll post it. It made for interesting reading.
If you assume no possibility of prize sharing its a straightforward computation to come up with expected return. Yes, at times when the jackpot is large enough then the expected (non-shared prize) value of a ticket is worth more than its price. Mathematically inclined investment groups have at times been able to make a decent return by trying to cover most or all of the numbers. Obviously this requires a nontrivial sized effort, and there is the danger of having to share the jackpot, which makes calculating true expected return impossible to nail down. Also lottery authorities don't want "investors" to win, they'd like the winner to be seen to be one of the schlocks who bets every lottery regardless of whether the odd are favorable (obviously most of the time they are not), these are the people who allow the lottery system make money for the operators. So they will try to disallow "investor groups" from claiming the prize.
You don't get the advertised prize. You either get the present value of the prize as a lump sum, or you get it over twenty years. Either way the EMV of the ticket is a lot lower than even the author proves, maybe only 60 pct of the calculated value. But, as observed earlier, you can improve your odds of winning it all by selecting your own numbers through game theory psychology, since all tickets are equally likely to pay off but not all numbers are equally likely to be bet on.
Just think if the odds were similar to the chance that the universal constants arrived at their particular and necessary settings by random drawing. Like 1 in 10 to the 500th power!
It is indeed very good that the 1 in 10^500 number is arrived at by blatantly dishonest people only and does not represent reality.
Just wanted to say thanks for the long-form article. I got up this morning to prepare a quick segment on this topic for a group of middle school Mathcounts kids and this not only saved me a ton of time...it's really an outstanding job, covering all the bases. Thanks!
Aah the joys of phone typing with only one thumb.
It's indeed good the odds are not 1 in 10^500 since then winning a lottery would be rare indeed but oh the roll over jackpot.
I'm sure sn was referring to lotteries, since that is the point of this post.
DP @12:
Not quite right. Ethan got it right in the full article: you either get the advertized prize paid out over 20 years, or you get some fraction of it up front. That fraction depends on the interest rate and typically varies between 50% and 60%. So when Powerball advertises a $100 million Jackpot, the winner will actually get ~$60 million up front or $5million/year for 20 years. Before taxes, of course. After taxes its probably about half that.
See Noevo:
Please show your work. Or was this rectal extraction?
eric, you probably know this but just in case: sn is one of the dishonest creationists who's been infesting Jason's blog: the number he gives is meant to "disprove" evolution by indicating there hasn't been enough time for evolution to have worked.
Its worth noting that in decision theory, the payoff is measured in expected utility, not expected dollar payout. These two are typically not proportional. So, for example, it is not strictly correct to say that the expected dollar payout from a $2 ticket must exceed $2 to count as a worthwhile investment. (Losing $2 might not detract appreciably from my quality of life, but gaining $100,000,000, might improve it considerably, in which case the expected gain is positive.)
This difference between cash value and utility also explains why it is often a good idea to pay insurance premiums, even though the insurance company rightly expects to make a profit from you. Paying insurance for low-value items that you can easily replace, however, localizes your transactions in a smaller, and therefore more linear, region of the utility v's cash value curve, and is hence not a good idea.
As someone has commented, lotteries are taxes on the stupid. That being said, I do play every once in a while. My reasoning is that a couple of bucks is not going to make a difference in my lifestyle or retirement funding. I just make sure that by the end of the year I have not spent more than about $40 on tickets. Anything more than that and I will beat myself up for what I could have bought with the money wasted on the lottery.
On the other hand, if I get lucky and win. Well, say no more.
Yes. However, analysis in the lower limit tells another story. 1/175,223,510 is infinitely greater than 0. 2*(1/175,223,510) is also infinitely greater than 0 but costs more. Determining if the cost of going from P=0 to P>0 is worth it is outside the scope of lottery gaming.
Notice the expected value of government-run lotteries is much less than the expected value of government regulated casinos. If you play correctly, the expected value for Blackjack (or 21) is close to 0.99, other casino games are in the 0.80 to 0.90 range. And the casinos make enough profit to pay their expenses and pay taxes (except in Atlantic City, where four went out of business).
@22: AIUI the casinos make something like 95% of their profit on whales (large money gamblers) and slot machines. They don't actually make that much money on table games such as blackjack and craps and would probably get rid of them in favor of slots...except that people like the way they look and they give the casino a more exciting rather than depressing atmosphere. IOW, they are window dressing. Yes they make money, but not anywhere near as much money per square foot as slot machines would. So the "expected value of a casino" is not the expected value of a properly played blackjack or craps bet, its much lower than that.
Of course, germane to this discussion is the fact that slot machines probably have an expected value higher than the lottery too, because the lottery odds are just that terrible. So spending that money in a casino is probably still a better bet. :)
I loved this article. I have wondered and done the math myself. Glad to see someone else also wonders about it. Although the chances are so slim to when I think it will still be sensible to play when the jackpot is extremely high because you have a chance to win if you play, if you do not play youtlr chance is 0. Love the math.
By saving the money with which you want to buy a ticket, you might become rich sooner than waiting for you luck with the lottery
I never really thought about it that way. It would better your chance though if you do the math.