"They say the universe is expanding. That should help with the traffic." -Steven Wright
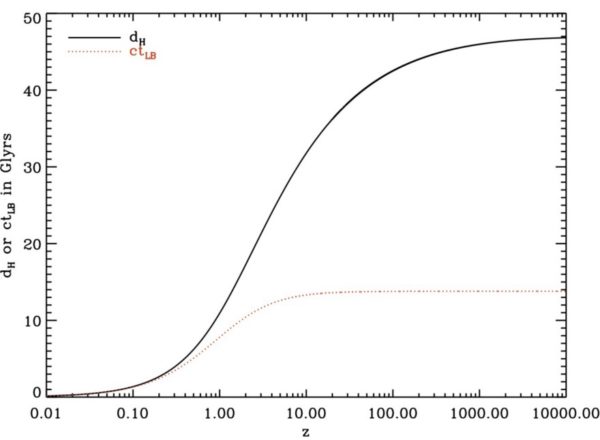
Look out at a nearby object in our Universe, and you'll find that the amount of time you look back (in years) is pretty much exactly equal to the object's distance (in light years). But look far away, and these two numbers start to diverge. In our 13.8 billion year old Universe, in fact, we can see back up to 46 billion light years in any direction. If you think this number seems absurd, you're not alone.
The GOODS-N field, with galaxy GN-z11 highlighted: the presently most-distant galaxy ever discovered. Image credit: NASA, ESA, P. Oesch (Yale University), G. Brammer (STScI), P. van Dokkum (Yale University), and G. Illingworth (University of California, Santa Cruz).
If the Universe were full of material everywhere and that material emitted light that was limited by c, you'd only be able to see for 13.8 billion light years. If you added in that the material could also be moving away from you at up to c, perhaps it could reach twice that: 27.6 billion light years. Yet the figure we have, 46 billion light years, only comes about because the fabric of space itself is stretching, a unique property of general relativity.
Special relativity (dotted) and general relativity (solid) predictions for distances in the expanding Universe. Definitively, only GR’s predictions match what we observe. Image credit: Wikimedia Commons user Redshiftimprove.
- Log in to post comments
More like this
@Ethan: Nice summary, and I do recall the naive R=3ct_H being one my homework problems (along with giant sapphire resonant frequencies :-). There's one observational issue for which your article begs the question.
How do we _know_ the distances so far beyond standard candles? It seems to me that we get the redshift distance from z, and from that the redshift age. But converting redshift age into "true comoving distance" involves making the GR assumption. Is there any obvious observational way to independently confirm the GR curve? Is that what "angular diameter distance" does for us?
@Michael,
Regarding your 'sapphire resonant frequencies' and the piezoelectric effect:
"The best-known application is the electric cigarette lighter: pressing the button causes a spring-loaded hammer to hit a piezoelectric crystal, producing a sufficiently high-voltage electric current that flows across a small spark gap, thus heating and igniting the gas."
https://en.wikipedia.org/wiki/Piezoelectricity#High_voltage_and_power_s…
Regarding resonance I have checked your suggestion of excited states of the proton such as Delta+, which is based on proton emission that can occur from high-lying excited states in a nucleus, where a proton is ejected from a nucleus. But these nuclear reactions are produced by colliding particles.
This is like hammering your sapphire crystal to produce sparks, applying pressure, generating heat. Thus the argument still stands that if heatwaves caused by the collisions of the LHC could travel towards surrounding matter, via the HiggsField, Dark Matter or such, for an extended period, than this could disrupt their nuclei and might cause an implosion.