"Despite its name, the big bang theory is not really a theory of a bang at all. It is really only a theory of the aftermath of a bang." -Alan Guth
Did the Universe begin with the Big Bang? When we discovered the cosmic microwave background, and its properties matched exactly the prediction of the Big Bang theory, it was a watershed moment for cosmology. For the first time, we had uncovered the origins to the entire Universe, having learned where all of this came from at long last. Emerging from a hot, dense, expanding, and cooling state, the matter-and-radiation-filled early Universe gave rise to everything we see today.
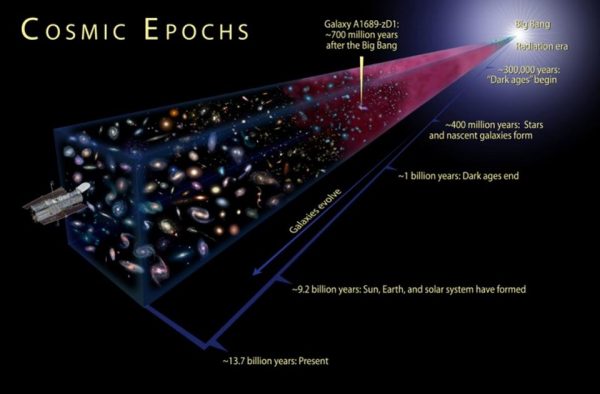 If you look farther and farther away, you also look farther and farther into the past. The earlier you go, the hotter and denser, as well as less-evolved, the Universe turns out to be. Image credit: NASA / STScI / A. Felid.
If you look farther and farther away, you also look farther and farther into the past. The earlier you go, the hotter and denser, as well as less-evolved, the Universe turns out to be. Image credit: NASA / STScI / A. Felid.
Except there were a few pesky problems that the Big Bang couldn’t explain. If the Universe truly emerged from an arbitrarily hot, dense state, and if space and time themselves were born at that exact moment, the Universe would have signatures that we simply don’t see. Instead, theorists came up with an alternative beginning: cosmic inflation. Inflation made a bold prediction about the scale and magnitude of the fluctuations that should arise from this early state, and when our technology finally caught up to our imaginations, we measured them.
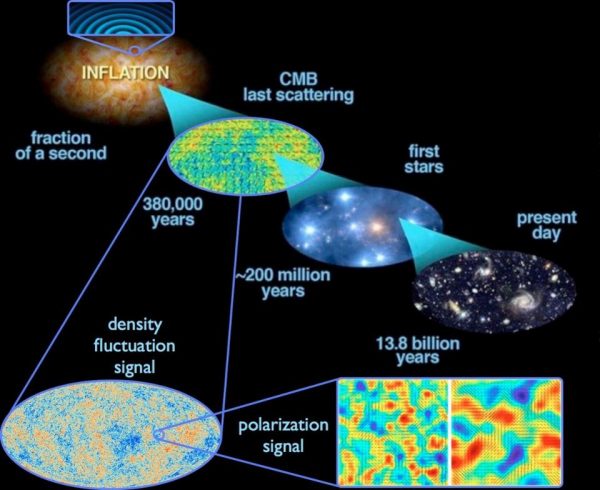 The quantum fluctuations inherent to space, stretched across the Universe during cosmic inflation, gave rise to the density fluctuations imprinted in the cosmic microwave background, which in turn gave rise to the stars, galaxies, and other large-scale structure in the Universe today. Image credit: E. Siegel, with images derived from ESA/Planck and the DoE/NASA/ NSF interagency task force on CMB research.
The quantum fluctuations inherent to space, stretched across the Universe during cosmic inflation, gave rise to the density fluctuations imprinted in the cosmic microwave background, which in turn gave rise to the stars, galaxies, and other large-scale structure in the Universe today. Image credit: E. Siegel, with images derived from ESA/Planck and the DoE/NASA/ NSF interagency task force on CMB research.
It turns out that the Universe didn’t begin from the Big Bang at all. It happened, but it wasn’t the beginning!

Do they have a theory on why it didn't happen earlier? Why didn't the Big Bang happen at the beginning? Why wait? What was it about expanding space that didn't allow a Bang then later did allow a Bang?
@Ethan,
Strange that you would discuss a few of the weaknesses of the Big Bang Theory now...when it suits you...only to replace them with something even more tenuous and unsupportable. You are almost literally pulling a real rabbit out of an imaginary hat and calling it science. Space time, like many other tortured terms in science such as 'quantum - insert unexplained phenomena here', or 'emergent - insert unexplained phenomena here', is not magic. It can't do the heavy lifting every time you can't explain something with the existing data and observation so that then you can claim your theory works.
.
Ethan,
If you can't tolerate critical opinion, you need to take down your response section. Filtering those you disagree with out of a conversation doesn't make you correct, it makes you corrupt.
Test. Am I allowed to comment yet, (third day not allowed to post) or am I secretly banned?
Another test. Not allowed to post... 3 days now.
When I learnt that space and time were created and were described as "it wasn't an explosion IN space, it was an explosion OF space', I concluded that the matter universe was created after the creation of space and time or spacetime.
In fact, in one of my books I did say that we had 2 big bangs: the explosion of space followed by the explosion in space which is the one that created the energy from which the matter universe was created. I even said that it posed a synchronisation problem.
It also meant that the material universe was expanding in the spacetime universe. Which also meant that scientists were wrong when they said there was no outside the universe because there's an outside to the material universe. Also, when they said there was no before the beginning, there was a before the beginning of the material universe.
Unfortunately, I disagreed with the explosion of space which meant that in my theory there was only one Big Bang that of the material universe which occurred in a void that's completely empty i.e. with no vacuum energy and it's the one that the material universe is expanding in. So, what was happening before the Big Bang is nothing. Time and space are not entities that need to be created all the time; let alone them being warped i.e. no spacetime.
You can't pull energy out of space time like a battery, or through some entirely bogus 'emergent' pretense, as all space time models are static and eternal, they have no beginning or end, so how would one suddenly do whatever it is Ethan is claiming? Space time is also a toy mathematical space, it isn't reality, it doesn't look like our universe, and it certainly can't contain more than one mass within its own design limitations, so it can't accommodate many masses (particles) suddenly popping into existence anymore than it can allow such a change in the first place, time is the geometry in the model, there is no 'and then', all time is all of one piece of the geometry.
Space time only contains whatever energy you initially place within the model. There is no way for it to decide to cough energy up for whatever reason that wasn't initially put there by the person running the model. Since the model can contain at most one mass, claiming such a model could suddenly produce multiple particles through some emergent behavior is nonsense, there is no emergent anything in space time since time is part of the geometry of the model, there is no free time parameter for change to occur within.
Ethan, I know that the universe is "flat," but when I think of that description I picture something like a very thin pancake or sheet of paper.
Since we live in a universe with 3 "travel” dimensions & time, combining to form space-time, that seems very different than "flat" to me.
I haven't been able to get a handle on the explanation of what a flat universe really means. Could you explain the answer to me?
Gee whiz Ethan, does that mean you may have to change your science blogs name to "Starts with an open question"?
:)
Test #?... My replies allowed yet?
Well it could've been happening before inflation, we just don't know. But it could not have been happening during inflation because the 'bang' requires normal physicochemical interactions between particles, and during inflation the universe holding those particles is expanding faster than light can travel between them, preventing any such interactions from occurring.
So (a) we wouldn't know if it happened before inflation and (b) it was physically impossible for it to happen during inflation, leaving the observed result (c) it happened right after the end of the inflationary period.
Cosmic Inflation and Big Bang Theory are not entirely different.
Cosmic Inflation is to Big Bang, as expansion of balloon is to opening the air valve attached to its tail.
Interesting, Denier. If expansion didn't happen, how would the universe have evolved? Would it have stayed the size of a basketball (or whatever)?
How does that even work, is it a 4-dimensional basketball, and atoms can fly around the entire volume without ever turning? Kind of like a 3D "Asteroids" game?
If that's what it was, would it just stay uber hot forever? No black holes form, even though the density is insane, because ... there aren't any gravity gradients?
Or maybe tiny variations in density eventually DO lead to the whole thing turning into a black hole. Then what? You have a 4D basketball with a Universe Black Hole (UBH) floating around?
Waaaaay too freaking weird. Has anyone seriously anaylyzed the "what if?" of no expansion?
Gee whiz Ethan, does that mean you may have to change your science blogs name to "Starts with an open question"?
All this continuing reification of space and time with no ontology of either! Why is the perfectly honest question, "What is space (or time)?" ignored by physics/ cosmology?
What evidence exists that space is anything other than the 3-D volume in which everything exists and moves? We *observe* "stuff in space" moving away, leaving more space in between and then we say, "space is expanding."
What evidence exists that time is anything other than the concept that it is not a static, frozen cosmos, i.e., that everything is moving and we have an agreement to say that movement takes time? That doesn't make it a malleable (dilating) entity, even when forces (gravity and acceleration) make clocks slow down as "timekeeping instruments."
Then of course we have Minkowski's model of a malleable "fabric of spacetime" which reifies both non-entity concepts as they magically coalesce into unity. And we call it mainstream science and present this "fabric" as an established fact.
Another comment still not posting.
Jim Paige,
My understanding of 'Flat' relates to how parallel lines behave.
In a flat geometry - which is the classical Euclidean formulation - two parallel lines never get closer or farther from each other.
Contrast this with the Earth, where two lines of longitude are parallel, yet get closer as you approach the poles.
This is hard for our limited brains to conceptualize when we apply it to space as a whole.
Universe being flat is about local curvature (or curvature of our visible universe). But that does not say anything about global geometry/shape of universe (which is obviously an important question).
Also consider that even as we see a flat universe around us, universe could still have any value of global curvature, if that global curvature is uniform everywhere. (Because if it is uniform it would be impossible to measure directly, isn't that right?)
I think one idea (main idea?) is a torus. I personally think it must be a 4d spherical surface (3d space curved in 4th (time) dimension).
@MobiusKlein #18
http://friesian.com/curved-1.htm
" What "curvature" would have meant to Euclid is now "extrinsic" curvature: that for a line or a plane or a space to be "curved" it must occupy a space of higher dimension, i.e. that a curved line requires a plane, a curved plane requires a volume, a curved volume requires some fourth dimension, etc."
What fourth dimension? Space is completely described by three axes.
Btw, regarding your "Contrast this with the Earth, where two lines of longitude are parallel, yet get closer as you approach the poles.":
They are not parallel if they converge. Arbitrarily calling them parallel doesn't make them so. Latitude lines are parallel, each making a circle on the globe, never converging.
Latitude lines are not "straight" or rather only the equator is. Longitude lines are "straight". Straight is defined as the shortest distance between 2 points, so only great circles are straight on a globe.
Mike,
Latitude lines are parallel circles around the globe. They don't converge. Longitude lines converge at the poles, therefore they are not, by definition, parallel.
Also, curved lines are not "straight." The shortest distance between the poles on a globe is "straight" through it, the polar diameter.
But I'm more interested in the non-Euclidean concept of more than the three spatial dimensions (axes). After 3-D space is completely described by the three axes, further dimensions (not counting "time") are just imaginary with no basis in the world of actual space.
We were (I thought) talking about the 2D geometry of a sphere not the 3D geometry of a ball. A straight line is defined as the shortest line that connect 2 points. A Geodesic. In the paraphrase of Euclid, for a plane there is one parallel line to a given straight line (geodesic) that runs through a point not on that line, for a sphere there are none and for a hyperbolic surface there are an infinite number
I'm not very interested in teaching elementary Euclidean geometry here. I'm way more interested in serious answers and discussion of my questions/ challenges in #16.
However, a sphere is described by 3-D geometry (for volume), same as a ball in the physical world. The shortest line connecting two points on the surface of a sphere (ball, Earth, etc) is a straight line through the sphere, not a curved line on the surface. Latitude lines can be considered as parallel circles, not straight lines, and there is no limit to how many can be drawn on a globe.
Finally (hopefully), on a plane there can be as many parallel lines as you care to designate. (Example: line-ruled notebook paper.) I'm done with that, but my challenge to describe a fourth ("non-Euclidean") spatial dimension stands.
MM
Any kind of geometry can be discussed. That most relevant to the earth's surface is clearly a 2D spherical geometry. In any geometry, a straight line is defined as the shortest distance between two points. On a 2-D spherical surface, that is a great circle; i.e. a path that if continued until it meets itself, would bisect the spherical surface. Lines of longitude are certainly straight lines, but in general latitude lines are not straight, with the sole exception of the equator. Consider airline routing, for instance. A flight from New York to Moscow most certainly does not fly due east along a latitude line, but instead flies northward toward the pole, and then back south from the pole to its destination. You also seem to have missed the "that runs through a point not on that line" part of Mike's post. In Euclidean space, there is only one line parallel to a given line running through a given point not on that line. In spherical space, there is none, in hyperbolic space there are infinitely many, just as Mike stated.
As for application to the real world, well in one sense, who cares? If your speaking solely in mathematical terms whether or not the mathematical system corresponds to anything in the real world is not relevant. It's still valid mathematics. It just can't be used to predict anything in the real world.
As for more than 3 dimensions in physical space, sure there is no experimental evidence for it. That does not preclude the possibility, though. There is a possibility that is seriously considered by physicists that the "extra" dimensions could be very small so that they are unobservable by ordinary measurements. Think of watching a tightrope walker from a long distance away. If you judge solely by what you can observe of him, you would reach the conclusion that he is constrained to move in one dimension (if he's good at it and not suicidal, that is). His "extra" dimensions are just much smaller than what you can observe. In similar fashion, we cannot rule out the possibility that there are more than 3 spatial dimensions, but that only three are large enough to observe. That, of course, does not make the existence of "extra" dimensions true; it just means we cannot conclusively rule them out.
Another possibility is that all the interactions that we can observe are limited to 3 dimensions. The strong nuclear force, the electroweak force, and gravity cannot be used to observe the extra dimensions. If you've ever seen "brane world" hypotheses, that is the basic idea of them. We don't see these extra dimensions because we cannot; there's no way to observe them with known interactions. Again, this certainly does not demonstrate the truth of these dimensions, but it does mean that we cannot just reject theories that predict more than 3 dimensions based solely on the fact that they make that prediction.
The curvature of space most certainly does not predict the existence of a fourth spatial dimension, however. I know the objection; if space is curved, what is it curved in? The truth is that curvature really is just a shorthand for "deviation from expected Euclidean geometry". IOW, the geometry you learned in high school is NOT the geometry that applies to the real universe. It is only an approximation.
For instance, you undoubtedly learned in high school geometry that the sum of the angles of a triangle is two right angles. If you were to make measurements of that sum with actual physical triangles on earth, you probably would find that the experimental results agree with the theory. However, if you were to make measurements on large enough triangles, clearly you'd find that the statement from geometry class is completely wrong. As an extreme example, consider the triangle formed by two longitude lines extending from the equator to the north pole plus the portion of the equator joining them. (Note that these are legitimate lines in a 2D spherical geometry). Clearly the longitude lines form 90 degree angles at the equator, and there is a nonzero angle at the north pole between them. The sum of the angles in this triangle is therefore greater than two right angles.
That simply indicates that the surface of the earth is curved, as we well know. Even were we unable to detect an extrinsic curvature in three dimensions, we would conclude that the earth is curved. This extrinsic curvature is very different from the intrinsic curvature defined by deviation from Euclidean geometry. For example, the surface of a donut clearly is extrinsically curved. However, it has zero intrinsic curvature; it's geometry is Euclidean. This is easily seen by taking a piece of paper (clearly flat!) rolling it so that one side touches the other to form a cylinder, then taking that cylinder and joining its ends to form a torus. The geometry of the lines, angles, etc. on that sheet of paper is unaffected by the process of rolling it to form the torus; the torus is uncurved.
The experimental question is then whether or not the universe is Euclidean or curved. At large scales, it appears to be flat, but it seems to be locally curved. It doesn't need to have more than 3 dimensions to have intrinsic curvature locally, although, as I stated before, that cannot yet be ruled out.
@ MM
"I’m not very interested in teaching elementary Euclidean geometry here." ... "The shortest line connecting two points on the surface of a sphere (ball, Earth, etc) is a straight line through the sphere, not a curved line on the surface. "
Maybe you should be interested in teaching yourself some basic math/geometry first. Otherwise there's a poor chance you're gonna teach anyone anything.
Sean T,
Briefly, not intended to cover your whole essay:
Re: " That most relevant to the earth’s surface is clearly a 2D spherical geometry. In any geometry, a straight line is defined as the shortest distance between two points. On a 2-D spherical surface, that is a great circle"
A point is a locus with no dimension. A line is one dimensional. A plane is two dimensional. a volume is three dimensional. Regardless of scale (size) volume is completely described by three dimensions (axes.) Any more are imaginary with no referent in the physical cosmos, as per scientific realism.
A straight line is not curved. All lines on the surface of a sphere are curved. So "2-D spherical geometry" is nonsense, as is any claim of a 2-D spherical surface. A "curved plane" is nonsense, as such curvature requires 3-D volume in which to curve. The surface of a globe or any part thereof is a 3-D object, not a 2-D plane.
@Sean,
What MM objects is accepting time as the 4th dimension, as in Relativity.
@Sean T and Frank: In fact, Michael Mooney has demonstrated that he objects to 19th Century and later mathematics, and probably objects to celestial navigation and even to the spherical earth.
I quote, "A plane is two dimensional." ... "A straight line is not curved."
So MM clearly rejects spherical geometry (latitude and longitude), the calculation of great circles for navigation, not to mention the entire mathematical subjects of differential geometry and topology.
It is utterly impossible to communicate with such a person, because they are essentially rejecting the foundations of mathematics for the past two or more centuries.
Michael Kelsey,
I urge you to read Kelley Ross's paper on the Ontology and Cosmology of Non-Euclidean Geometry @
http://friesian.com/curved-1.htm
Btw, I have argued (nearly to beating a dead horse) that Earth is in fact nearly spherical... this as scientific realism (with full-on empirical epistemology) debunking special relativity's claim that a flattened ("pancaked") Earth is an "equally valid" description because of length contraction depending on the velocity of an approaching observer.
I explained that longitude lines converge at the poles, therefore not parallel while latitude lines don't converge.
If you disagree with the elementary geometry of planes (2-D) and straight lines (not curved as lines on a globe), then make your case.
I hope you are open to learning some ontology of geometry (from Euclidean to non-Euclidean) from reading Kelley Ross's paper.
@Frank; #28
You can call time a "dimension"(time passes as everything moves) but we were speaking of an (imaginary) fourth spatial dimension. (Computer glitching)
Michael Mooney, a retired bricklayer from Oregon, tells a senior PhD HEP physicist that he ought to learn some geometry... that's cute. Talk about ego-narcisist.
Neither personal attacks or appeals to authority /credentials are relevant to the *content* of scientific debate or discussion.
(Aside)
I don't know where SL got his/her background on me but it is... let's say... incomplete and totally mis-representative.
I leave it to Michael Kelsey to reply to my #30 if he wants to discuss the development of non-Euclidean geometry.
Science is "nothing personal."
"Neither personal attacks or appeals to authority /credentials are relevant to the *content* of scientific debate or discussion."
- no personal attacks, just observation. As for relevance in discussion, and possibly deciding who's right and who's not, credentials and professional experience are very much relevant. Hence why you don't see i.e. opera signers in a role of medical experts in courts.
"I don’t know where SL got his/her background on me but it is… let’s say… incomplete and totally mis-representative."
- well you've put it online in more then one place, I just googled. Took about, ooh, 5 seconds. But good to know that you are totally mis-representing yourself on your own profiles.
SL,
If you are hell bent on slander ("no personal attacks" of course), it's time for you give examples of my alleged mis-representation ... or stuff it.
I have clearly stated that I am a retired psychologist (and mason) and that science has been an avid interest all my adult life, contributing as a free thinker (no job to lose) where I can without science credentials... and that I am a scientific realist, committed to honesty in science,
" it’s time for you give examples of my alleged mis-representation … or stuff it. "
LOL. Do you hear yourself? You said it was "incomplete and totally mis-representative.", not me. And they are your profiles, not mine. Guess it's time for you to argue with yourself and decide who you are.
SL,
Give one example of my misrepresentation of myself or go away. I have been and remain totally honest in my comments in this forum.