“If the doors of perception were cleansed every thing would appear to man as it is, Infinite. For man has closed himself up, till he sees all things thro' narrow chinks of his cavern.” -William Blake
When it comes to the ultimate question of the size of the Universe, we have to look to greater scales than what we can possibly observe. Although we can place constraints on how big the unobservable Universe must be, coming up with a lower limit to its overall size, there’s a bigger question that we don’t yet know the answer to: is it finite in size, or is it truly infinite?
 The observable Universe might be 46 billion light years in all directions from our point of view, but there's certainly more, unobservable Universe just like ours beyond that. Image credit: Wikimedia Commons users Frédéric MICHEL and Azcolvin429, annotated by E. Siegel.
The observable Universe might be 46 billion light years in all directions from our point of view, but there's certainly more, unobservable Universe just like ours beyond that. Image credit: Wikimedia Commons users Frédéric MICHEL and Azcolvin429, annotated by E. Siegel.
Beyond what we can see, there ought to be more Universe just like our own, originating from either the same Big Bang, or possibly, if inflation is correct, from other Big Bangs at later or earlier times. And thanks to the ideas of eternal inflation, we have very, very large numbers for what’s possible as far as size goes. But there’s a long way from very large to infinite, and determining whether that’s true is a very difficult prospect.
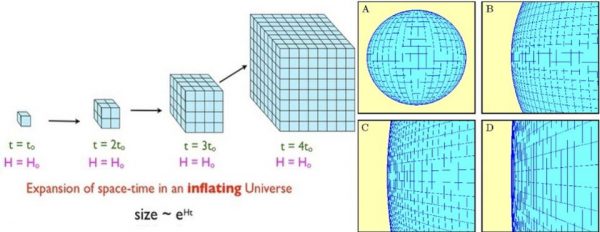 Inflation causes space to expand exponentially, which can very quickly result in any pre-existing curved space appearing flat. Image credit: E. Siegel (L); Ned Wright's cosmology tutorial (R).
Inflation causes space to expand exponentially, which can very quickly result in any pre-existing curved space appearing flat. Image credit: E. Siegel (L); Ned Wright's cosmology tutorial (R).
So what can we say about the conditions under which the Universe is either finite or infinite in extent?

Although the domain of Science does have bounds, it remains an excellent tool for exploring Nature.
Nice.
This bit
is (to me) one of the strongest descriptions of the scales you discuss.
I'll start with the big one:
"The answer to the biggest of all questions, of whether the Universe is finite or infinite, might be encoded in the Universe itself, but we can't access enough of it to know."
Reason and logic are still a vital part of the epistemology of what we know and how we know it.
If one claims that the universe is "possibly" finite, one must explain/define the "possible" boundary... what it IS... and then what lies beyond that imaginary boundary.... What else but more space with more stuff in it, ad infinitum?
Now to the 'what if' speculation leading to this 'what if' conclusion:
"One such piece of info is a startling fact: the curvature of space, as best as we can tell, is completely flat. If space were positively curved, like we lived on the surface of a 4D sphere, distant light rays would converge..."
So "... fact: the curvature of space... is completely flat." (A blatant contradiction.)
A plane is flat. Curvature of a (former) plain requires 3-D volume. What is a 4-D sphere? A sphere is 3-D geometry.
If we "lived on the surface " of a cosmic sphere, what would exist inside the sphere? Non-Euclidean (imaginary) geometry is not an established universal fact describing the real physical cosmos.
"...the universe was creating new space so quickly...
a probability that inflation will continue, creating more and more space."
What does "creating space" mean and what is the real- world process? If space is infinite, and how could it not be, considering above comments, then "creating space" is total nonsense, especially considering that "inflation" is a theory abandoned by its creator but still being presented by Ethan as consensus science.
"These are calculations we know how to do (given certain assumptions), and they lead to an inevitable conclusion:..."
Good one!... an inevitable conclusion based on certain assumptions. If your assumptions are wrong your conclusion will be wrong too, not "inevitable."
Now to the bottom line:
"In fact, unless inflation went on for a truly infinite amount of time, or the Universe was born infinitely large, the Universe ought to be finite in extent."
So, unless a very questionable theory has been eternally operating or the universe is in fact infinite... then it "ought to be finite."
Maybe you should stick to "scientific explanations" of science fiction.
Or, perhaps, did all of space and time emerge from nothingness a finite amount of time ago? These are all possibilities"
@Ethan:
"If space were positively curved, like we lived on the surface of a 4D sphere, distant light rays would converge. "
Think of surface of a 3d sphere first:
It is a 2d surface curved in the 3rd dimension.
Now think of surface of a 4d sphere:
It is a 3d surface curved in the 4th dimension.
What if Universe is surface of a 4d sphere where 3d surface (space) curved in the 4th dimension (time)?
So is it really not possible, 3d space we see using our telescopes, could be flat in those 3 dimensions of space, but curved in time dimension?
" fact: the curvature of space… is completely flat.” (A blatant contradiction.)
A plane is flat. Curvature of a (former) plain requires 3-D volume. What is a 4-D sphere? A sphere is 3-D geometry"
MM, if you don't understand the basics of the mathematics (and you clearly don't) and how the terminology works you shouldn't try to bullcrap your way through.
"Now think of" unicorns. "What if" they were "real in another dimension?" And IF they had wings like Pegasis, the flying horse, we could ride unicorns in the sky!
Not even close to science, but very much in synch with this blog. "Anything you can imagine is possible." (The universal gullible fool.)
@Frank #4,
There are no curvatures in one dimension, just a straight line. If you bend it or curve it, you must employ a second dimension to describe it, or else, how are you representing your curve? your change in x over your change in y? The information to describe your curve IS contained the second dimension, the y plane. No y plane, well, you ain't got no curve then, logically, geometrically, mathematically, or otherwise. Employing non-Euclidian geometry is also a cheat, you are merely side stepping the fact you are playing with a higher dimension than claimed by calling the initial space curved, saddle shaped, torus shaped, banana shaped, ad nauseam. Hand waving and saying 'imagine that ' blah blah blah changes nothing. Offsetting your curvature in the math to pretend you aren't curving (when you are) like a hidden variable, or imagining something doesn't make it become so, especially when it is already defined logically and geometrically. Sleight of hand and deception is also unbecoming in a physicist...though it is just par for the course for mathematicians historically.
.
A two dimensional space does not have a 'surface', unless you are being euphemistic and placing your actual perspective in the third dimension, and even then it is still a flat plane. A two dimensional space can contain a curved line in the x y plane only. If you attempt to manipulate anything in the plane outside of x y, you are no longer representing something in two dimensions, but in three dimensions, as you would have no other way to describe how much something was outside of the x y plane except in terms of the z plane. To say otherwise is misdirection or nonsense using the same misdirection as was described above, calling a curved space flat so you can pretend you aren't dealing in a higher dimension is just a con. When you do anything to a two dimensional space that can't be described in x and y, and require another degree of spatial freedom, you are now in three dimensions. Hand waving does not change the rules of how much information it takes to describe a three dimensional object, neither does imagining them otherwise or envisioning them so after too much drink or pot smoking.
.
When you are in three dimensions, there is no way to describe a spatial curvature outside of three x y z dimensions without creating a contradiction, you would just be overlapping or 'clipping' into an already described space. Treating a three dimensional space like a two dimensional space is meaningless except in a representational diagram or image, like a drawing or a 3D image rendered on a monitor. There is no way for a three dimensional space to be compressed into a two dimensional space without losing most of your information. Perspective in art uses geometry to create only the illusion of depth on a flat (or curved) surface if viewed from a particular angle, but even this three dimensional surface can not contain all the information, it's just an optical illusion, you cant walk around the object or view it from a different angle without ruining the illusion, tricking the eye is not altering reality, or changing dimensionality. At best, if you were to take a two dimensional 'view' of a three dimensional space, you would get something like an MRI cross section image, except that your 'slice' is of zero width, even if you could still somehow look at the cross section, it would be like comparing a single digit to the rest of the entire number line, you would have only the tiniest part of what you were trying to represent.
.
Mathematicians and physicists often play fast and loose with the word 'dimension', they enjoy doing so. There is a vast difference between an actual spatial dimension (of which there are three) and a dimension of particular type of measurement like a laundry list of attributes, such as neck size, waist, inseam, chest, or part of a very long address of some kind, Country, state, region, country, city, street, building number, unit number, specific room, in a particular cabinet, in a particular drawer, compartment, etc. You can plonk as many of these sub headings as you like in your matrix and call it a 'dimension' if you like, but they are not spatial dimensions. Time as expressed in math and calculation is not equivalent to the x, y, and z spatially ,it is a rate of change, a ratio, and it can't be treated as x, y, and z are spatially. To do so would create the delusion that time was somehow spatially and geometrically orthogonal in relation to the x, y, and z planes, which it isn't. Just because you can stick values in a 4D graph does not mean reality functions that way, any more than a funhouse mirror means you have lost or gained weight.
.
The silly conclusions of physicists that are calling for 'multiverses' is the product of their treating reality as if it was a function of their 4D graph. They are mistaking their limited conventions of modeled representation with how reality functions, much like treating an M.C. Escher engraving as a description of reality that would be possible. For some visual eye strain, watch the INCEPTION movie where they play perspective looney using CGI. The Doctor Strange movie is just following in their lead, but uses some of the same optical misdirection.
Imagine moving away from here at the speed of light, double it by 10, and keep om moving forward, double it by a hundred, a million … swooof … faster and faster … you just can keep on going … further and further forever … because there's no end to it … far out … infinitely … until you fall asleep. ?
@dean #5
"MM, if you don’t understand the basics of the mathematics (and you clearly don’t) and how the terminology works you shouldn’t try to bullcrap your way through."
From my #3
'Non-Euclidean (imaginary) geometry is not an established universal fact describing the real physical cosmos.'
I understand the terminology and the history/ ontology of non-Euclidean geometry. Do you? Here again is a link to a thorough paper on it by Kelley Ross in case you haven't read it.
http://friesian.com/curved-1.htm
@CFT #7,
First let me try to better explain what I mean exactly:
Let's first simplify the problem:
Assume our universe was 2d, as the surface of a 3d sphere. Now latitude and longitude are our 2 space dimensions. Our distance from the center of the sphere is our time dimension.
Since our universe is the surface of a 3d sphere, it has a general uniform positive curvature, depending on our time coordinate, anytime.
Now the big question is this:
As beings of 2 dimensions now, can we directly measure the global uniform curvature of our universe in any possible way? Or asking the same question in another way would be this: Our universe would look curved or flat to us?
If speed of light was high enough, and if we had an astronomically powerful laser, we could send a beam in any direction, and later see it came back from exact opposite direction, sometime later.
Then we would know for certain our universe if finite.
But I claim, we still would not know what is the general curvature of our universe.
Could we really find/measure it by observing the stars or galaxies around, in our 2d universe?
For answer, first realize we don't know any poles for our universe. We can use any point in our 2d universe as our North Pole, would it make any difference for coordinates/measurements/observations?
Then why not take our location in our 2d universe as the north pole of our universe.
Now try to imagine all longitude lines coming into our location (the north pole our coordinate system) as the star/galaxy lights.
Can we really see/measure the general curvature of our universe from those light beams coming to us from every direction we can see?
I claim the answer is no.
Why? I claim, as long as we are making all observations and experiments, to calculate the general curvature, using only our space dimensions (latitude and longitude),
we would always find it to be perfectly flat in those 2 dimensions. I also claim, we could calculate the general curvature of our 2d universe (latitude and longitude), only if we include the precise time coordinates in the measurements/experiments, as well as precise latitude and longitude coordinates.
So I really claim, our universe looks flat to us, because we are making all observations/measurements in 3 space dimensions. But if we also include time coordinates, then we can calculate true general curvature of our universe.
And I further claim:
Curvature of circle (1d curved line on 2d space):
1/r
Curvature of sphere (2d curved plane on 3d space):
1/r^2
Curvature of sphere (3d curved space on a 4d space):
1/r^3
So if our universe was 2d space and 1 time (2d curved plane on 3d space):
Its general curvature at any time would be:
1/r^2=1/(c*t)^2 (where c is the speed of light and t time passed since The Big Bang in seconds)
And so if our universe is 3d space and 1 time (3d curved space on 4d space):
Then its general curvature at any time is:
1/r^3=1/(c*t)^3 (where c is the speed of light and t time passed since The Big Bang in seconds)
And I further claim:
If astrophysicists recalculated general curvature of our universe, by including all space and time coordinate information correctly, then they should be able to verify, the calculation results always match to the theoretical value which is 1/(c*t)^3 .
The raw data to use for those calculations would be the pictures of universe, for the same direction, looking at views there from different times.
I realized this value for the current general curvature of our universe (1/(c*t)^3) would be correct only if we ignore the expansion of the universe. To get correct values for any time, we need to use current radius of the universe for that time, including effect of the expansion until that time.
Wikipedia says:
"it is currently unknown whether the observable universe is identical to the global universe"
From what I claimed above, I claim they are identical.
(So if the current radius of observational universe is 46 Bly, then I claim it means current global curvature of our universe is 1/(46 Bly in meters)^3.)
I am struggling with how to think about 'other big bangs'. There is nothing, not even space or time, then there is our big bang, the expanding universe and outside of that no space and time.
What does it mean to talk of 'other big bangs' which I presume you mean to be outside of our time and space? Can they 'overlap' with ours and what does that mean when there is no space and time between them? This is part of me trying to visualize and understand why we can set an upper limit to the size of our universe when we know when the big bang was, the speed of light and the expansion rate. Help!!
thats why we CANNOT set an upper limit - sorry.
@Frank #10-#15,
I will do nothing of the sort.
I will not 'assume' a 3D anything is actually 2D, anymore than I would 'assume' 3 was actually a 2 in disguise.
Perhaps you should refresh yourself on the difference between one number and the next on the number line, they aren't interchangeable because your answer isn't working otherwise. Imagination has nothing to do with changing the difference between a two and a three, or conflating one dimension with another because your math requires it. You are stating that flawed mathematical convenience and convention determines reality. I'm saying you really need to come back to the real world. In the real world, one thing does not become another because you imagined it.
.
You are also playing the calculus game, pretending if you expand an image as much as you like everything is a straight line. Well, it isn't, it's a crude approximation only. This is no different than saying if I look closely at the ground, the earth is actually flat. It isn't.
.
While a person might 'act' two dimensional, if you are a human being, you nor anyone else has ever existed in just two dimensions, and can't as you are composed of highly structured atoms. I have as of yet to encounter an actual two dimensional object that wasn't just an imagined abstraction. Something can't even exist as an abstraction unless someone is carrying it around in their three dimensional brain and thinking about it. I also have no interest whatsoever in magic or spontaneous miracle driven hypostatizations that you have imagined. I'm interested in causality and the measurable processes over a period of time which can be observed and predicted without divorcing myself from reason.
@CFT #18:
"I will do nothing of the sort."
Nobody is forcing you to anything here.
I was just offering my thoughts for you or anyone else interested.
@Michael Mooney #9,
The dirty little secret is, all Non-Euclidian geometry logically depends upon Euclidean geometry as a foundation. All other geometries are extensions of Euclidian with different starting topologies. To make any other topology work, you still must have external Euclidean reference points to even see how your new topology diverges. It is impossible to measure a curve accurately except in relation to something that is not 'curved', else lengths, proportions, their and relations are meaningless taffy. Sure you can base your assumed starting geometry off any silly shape you like, spheres, cylinders, saddles, donuts with sprinkles if you like, but in the end you would still have to have to depend upon Euclidean geometry as your underlying starting point to make any sense of the others possible. The reverse is not necessarily true however, this is much like saying you have invented imaginary numbers so they supercede common integers, which is nonsense. Stacking another layer of abstraction on top of Euclidean geometry has some uses for specific topological problems, but it has even more mis-uses, namely, making thing more complicated than they need to be, mostly for the purposes of making it harder to analyze and easier to hide behind. Einstein only used hyperbolic math in his theory to begin with because he was advised to do so by some of the mathematicians he was friends to and consulting with. They had their own pet 'ideas' they wanted to get attention, and hitching their wagons to Einstein's rising star seemed the pragmatic choice, there were suggestions doing so might even make Einstein's rather simplistic looking formula look more sophisticated...and harder to critique by his already numerous detractors. Sadly, this kind of mathematical misdirection has become common and taken on a life of its own now, to the point where even Feynman felt it was getting out of hand, and called it out, despite the fact he actually used gradations of similar kinds of things to hide his own mathematical pushes behind.
CFT, Agreed.
Non-Euclidean geometry started with creative imaginations taking Euclid's parallel lines and claiming that they can intersect.... IF... Of course, then they are not parallel anymore, but what the hell! Then, with more imagined "degrees of freedom" it's off to "4-D space" which is nonsense since three axes completely describe space (volume.) But now all of the above is so completely cannonized by the ruling elite in math and physics that any critic is immediately dismissed as a moron (not up to date with physics) without even considering the argument, or the thorough analysis of the ontology as by Kelly Ross. No serious discussion of that paper here, though I've provided the link a few times.
MM, the fact that you and the other deniers are not capable of understanding the mathematics doesn't mean the mathematics is bogus or meaningless.
It means you won't put in the hard work.
Thanks for confirming that you are not here for scientific discussion. You are now on my 'no reply' list... if I remember.
"Hard work" seems to be your working mantra to elevate you above all lazy philosophers/ psychologists who never specialized in math... the elite club.
(I still know that a fraction of 1 is not 1.)
MM, the repeating decimal of 9s is not "a fraction of 1 " because there is no "end" to it -- it is 1. That is the point. I cannot believe you can claim to understand the mathematics of relativity if you cannot grasp a concept that is taught at the latest in first semester calculus.
" philosophers/ psychologists who never specialized in math"
If you want to comment on math related issues you need to know the basics the math. You don't.
9.999,,,, reasons that .999... = 1
https://www.khanacademy.org/math/math-for-fun-and-glory/vi-hart/infinit…
So when there is no end to how close the repeating .999 decimal gets to 1, the convention is to call it 1. But no matter how close it gets to 1, it's still not there yet. Like .999 % of a pie still has an ever-diminishing missing slice gap.
Again, math is meaningless when it has no reference to the real world. But many mathematicians (like here) are ok with that. Dividing by zero sounds like fun too.
Ps: One can understand the fallacies of relativity without dong the math.
If you are approaching Earth at about .86c, they say you will measure its diameter in the direction of the approach to be about 4000 miles. But that still doesn't make Earth flatten out to half diameter in that direction.
@MM #27:
You just denied all of physics then :-)
Because if .999... is not equal to 1 then math of limits is wrong. If math of limits is wrong then calculus is wrong. And then Newton Physics, QM, Relativity is wrong.
@Frank #28: He basically denied an understanding of basic arithmetic. You can explain simple numeric limits like that (think the Hilbert Hotel) to a bright fourth grader and they'll understand it and be able to apply the idea elsewhere.
MM,
I must agree with others; your knowledge of math is flawed. Non-Euclidean geometry most certainly did NOT come from saying "parallels can intersect". It came from a careful logical consideration of Euclid's original postulates. These were:
1. A line can be drawn through any two points.
2. A given line can be extended from its endpoint for any distance.
3. All right angles are equal (right angles were previously defined without reference to angle measure)
4. A circle can be drawn centered at any point with any given radius.
5. If two lines are cut by a third, the two lines intersect on the side where the third line makes interior angles whose sum is less than two right angles.
Non-Euclidean geometry developed when mathematicians started questioning whether these postulates are independent. It was believed, in particular, that the fifth was implied by the others. It was discovered that this was in fact not true, and that all the postulates are independent. That led to new geometries with modified fifth postulates.
Now, the fifth postulate is somewhat obscure as originally stated, but it is in fact logically equivalent to the proposition that given a line and a point not on the line, a unique line parallel to the given one through the given point can be drawn. Essentially, two types of non-Euclidean geometry developed from modifying this; that no line can be drawn parallel to the given one through the given point or that more than one such line (and possibly infinitely many) can be so drawn.
Both of these modifications lead to internally consistent axiomatic systems. There are no inherent contradictions, so they were deemed worthy of study by mathematicians. Your objection that these don't correspond to the real world is irrelevant; mathematicians studied them purely as deductive systems.
Of course it was immediately realized that the first of these types, the no parallel lines one, fitted the geometry of the earth's surface quite well. Lines were defined on the surface of the earth as the path of shortest distance between two points, i.e. a great circle route. It's quite clear that with that definition, all lines will intersect. Obviously, when viewed in three dimensions, the earth's surface can be seen to be a curved surface. By extension, any space described by a non-Euclidean geometry is now called a curved space, regardless of dimensionality.
The question then arises, of course, what is the actual geometry of the universe. You want to duck this question and just assume that Euclidean geometry applies. There is absolutely no logical reason that this must be true, however, as I have stated above. There is nothing logically contradictory about non-Euclidean geometries. The question of which is the best description of the universe is an empirical one, best addressed by science. Science has in fact done so, and overwhelmingly the answer is that non-Euclidean geometry applies.
The other question also demonstrates your lack of understanding as well of the notion of limits and infinite series. The number 0.9 is obviously less than 1. 0.99 still is. 0.999999999 is as well. A number expressed by a decimal point followed by any FINITE number of 9's is less than 1. However, a number expressed in decimal notation is in fact a sum of a series: 9/10 + 9/100 + 9/1000 + 9/10000.... The sum of a FINITE number of terms of that series indeed is less than 1. However the sum of the entire INFINITE series is equal to 1. An infinite sum is not the same thing as a sum of a finite number of terms, no matter how many terms are added.
If you doubt the above, consider the old Zeno's Paradox. Zeno argued that motion is impossible. He argued that to get from point A to point B, one must move first from point A to a point halfway between A and B. After that's accomplished, there is a new midpoint between the first one and point B. One must reach that point. But no matter how many times you move halfway to point B, there will be a new point halfway between your location and point B that you must reach. Therefore, you can never reach point B.
Making this more mathematical, suppose the distance between A and B is 1. Then Zeno is arguing that you must move through a distance of 1/2 first, followed by a distance of 1/4, followed by 1/8, etc. Equivalently, 1/2 + 1/4 + 1/8= 7/8 <1. No matter how 7/8 + 1/16 = 15/16<1. 15/16+1/32=31/32<1, etc. No matter what FINITE number of terms you add, you can never travel 1 unit and reach point B. However, we obviously CAN move 1 unit from point A to point B. This strongly suggests that the INFINITE sum 1/2+1/4+1/8+1/16... actually is equal to 1, a fact which can indeed be mathematically proven.
If you STILL doubt, then do the following. Express 1/3 as a decimal. Multiply it by 3. What do you get for your answer? Obviously 1/3 x 3 = 1, but if you do what I suggest while adhering to the formal rules of multiplication, you will get a "different" answer than 1.
Ok, folks. I am not a mathematician, but I do understand the concept expressed by Sean T as follows:
" The sum of a FINITE number of terms of that series indeed is less than 1. However the sum of the entire INFINITE series is equal to 1."
However, "in the real world" there can be no infinite series. Keep adding nines for eons and you still have more to go, forever... still not one whole pie (assuming that the purpose of numbers is to quantify "things in the real world.")
I think that Zeno's paradox illustrates the difference between math abstractions and said real world. If you are arbitrarily limited to move half the distance at a time between two points, you will never reach point B. But of course that is an imaginary restriction, as " we obviously CAN move 1 unit from point A to point B."
Same with the pie. Closing the gap by adding another 9 endlessly just leaves an ever smaller gap... still not one whole pie.
Not to say infinities and zeros don't have their math uses for approximation and "place keepers" (zeros) but "divided by zero" is meaningless and an "infinite series" is never complete... as in "equals 1." One what?
That's the best I can do for a reality check as a reasonable and intelligent (if IQ tests are valid measurements) non-mathematician.
Speaking of reality checks, how about the math of the " Lorentz transformation" transforming Earth into a big flat pancake?
@MM # 31:
"However, “in the real world” there can be no infinite series."
You still don't understand. Even Newton Physics depends on them for solving many basic physics problems.
For example, how do you think Newton's Law of Gravity explains elliptical orbits of planets? It requires calculus which requires solving equations with infinite terms. So if you don't accept solution values calculated similar to .999...=1 then so many solutions become impossible. :-)
MM,
"In the real world there can be no infinite series"
Really? How do you know this? You seem to like to make a lot of unsubstantiated assertions. My Zeno's Paradox example IS an example of a real world infinite series. Do you not have to pass through the midpoint of an interval to move from one endpoint of the interval to the other in the real world? If you live one mile from where you work, do you not have to get to a point that is a half mile from each? Once there, do you not have to reach a point that is a quarter mile from work? Do you not then have to reach a point that is an eighth of a mile away, and so on?
Why can you not pass through an infinite series of such points in the real world? For any two points, we can find a point between them. We can then find a point between that new point and the end point. We can continue this indefinitely. That's why Zeno's Paradox was troubling to many people -- they though like you do that there is no such thing as a "real" infinite series. The most likely objection is that passing through an infinite series of spatial points would require an infinite time to accomplish. That objection, however, is muted once we accept infinite sums of series. If we travel at a velocity of 1 unit, we will reach a distance of 1/2 units in 1/2 of a time unit. We reach the next midpoint in 1/4 time units. The next in 1/8 time units, etc. We get the same infinite series of times that we did of distances, so the same infinite sum, namely 1 unit is obtained. This tells us what we already knew; it takes 1 time unit to travel 1 distance unit if our velocity is equal to 1 velocity unit.
In any case, what do you get when you multiply an infinitely repeating series of 3's by 3? 0.3333333... x 3 = 0.9999999... does it not? What fraction is equal to 0.333333.... again?
MM,
BTW, I am NOT going into the Lorenz transformation and the "pancake earth" thing with you again. It's been done to death. The observer moving rapidly WILL indeed observe a pancake earth. His description is physically valid; i.e. he will, if he tests them, find that all physical laws that are valid in your reference frame are equally valid in his. If you want to keep saying that "the earth is not really flattened" then you are welcomed to do so, but you have no scientifically valid basis to tell the rapidly moving observer that his observation is incorrect.
MM.
You seem hung up on the idea that numbers must be real for the real world. (Imaginary numbers are unfortunately named and are in fact real). To you infinity isn't real, even though in one of Ethans posts he talked about how the universe itself may indeed actually be infinite, for real.
So what do you make of negative numbers? How can they be real to you? For example would you be willing to accept from me minus three apples?
" but I do understand the concept "
No, you clearly do not
"Again, math is meaningless when it has no reference to the real world. But many mathematicians (like here) are ok with that."
No, the reason for the disagreement is not the fault of the mathematics or the people who do mathematics. It is due to your lack of understanding.
" Dividing by zero sounds like fun too.'
Further evidence of your lack of knowledge: division by zero is an undefined operation in arithmetic -- no value can be assigned to 100 divided by 0 nor to 0 divided by 0 as a result of basic division.
let me guess: you never mastered the concepts of limits or removable discontinuities either, right?
Drat the lack of preview. Final point MM: your claims about your fancy sounding education become more and more bogus the more you show your lack of understanding of the mathematics freshmen in college master.
Watch this again. It has Sean Ts stuff in it and more.
https://www.khanacademy.org/math/math-for-fun-and-glory/vi-hart/infinit…
I REALLy like number 7 - pushes me over the edge.
i.e. if you insist that 1 and 0.999... are different, then name a number thats between them.
@MM #33, You wrote, "Ok, folks. I am not a mathematician...", and yet you still have the astonishing arrogance to claim that you know more than mathematicians and physicists, without having any willingness to put in the effort to learn what they do.
One more point: mm has demonstrated that he doesn't have a grasp of the mathematics for the terminating and non-terminating representation of 1.
That leads to the obvious questions:
- does he not believe that we can represent some rational numbers in two decimal forms, one terminating the other not?
- if he doesn't believe in infinite series how does he explain the series used to calculate pi, or e?
His comment about mathematicians being fine with division by zero indicates he never learned the difference between basic arithmetic and the concept of limits.
And quite beautifully, I CAN name a number between them.
Its 0.00000000.........
Which equals 0. No difference between them.
QED :-)
@dean #37
What I wrote here about my education and original work in psychology is true. If you dispute that, show your evidence (there is none) or GET OUT OF MY FACE.
@Sean T #47
" The observer moving rapidly WILL indeed observe a pancake earth. His description is physically valid"
Disregard all Earth science to believe this bullshit.
Mm, the point is this: whether you have the education you named it not, it is clear you learned nothing about mathematics beyond simple addition, subtraction, multiplication, and division.
"That’s the best I can do for a reality check as a reasonable and intelligent (if IQ tests are valid measurements) non-mathematician."
IQ tests are not valid measurements of intelligence -- we've known that for some time. At least, most people have.
"“Hard work” seems to be your working mantra to elevate you above all lazy philosophers/ psychologists who never specialized in math… the elite club."
Odd. Most people would view not wanting to do the hard work as a failing. You wear it as a badge of honor.
@dean #45,
Please get off your high horse and quit being such a snob. There actually are some problems with the underpinnings of certain assumptions in calculus that do have logical ramifications. Even Ethan is wrong about a thing or two, Bee is calling him out on his repeated mischaracterization of inflation.
.
"But it’s unfair to pick on Jim because this oversimplification is so common. Ethan Siegel, for example, is another offender. He writes:
“if the Universe had any intrinsic curvature to it, it was stretched by inflation to be indistinguishable from “flat” today.”
That’s wrong too. It is not the case for “any” intrinsic curvature that the outcome will be almost flat. It’s correct only for initial values smaller than something. He too, after some back and forth, agreed with me. Will he change his narrative? We will see."
.
The entire article is here:
.
http://backreaction.blogspot.com/2017/10/i-totally-mean-it-inflation-ne…
.
So grow some humility in how you speak to others. Even the cotton picking 'experts' don't agree, as I've been saying all along in defiance of Ethan's false consensus. Consensus isn't about science, it's about politics.
@Michael Kelsey #40
You calling anyone arrogant is actually pretty damn funny. Look in the mirror.
@Steve Blackband #42,
Ever heard the phrase 'Close but no cigar.'?
Actually, you are mistaken. .999... is not a finite number, as you indicated with the "..." it is an infinitely repeating decimal. 1 is finite number. You would then be equating an infinite number with a finite number... not so smart for someone trying to make someone else look stupid. Technically, there are no infinite numbers except in abstract conjecture, as you would need to symbolically represent it with the infinity symbol placeholder, which is NOT a number, or by some mathematical representation like n+1, or a calculation of the number PI, or e, which is an operation that can not ever actually be completed since you most definitely don't have forever to do it.
.
If your .999 whatever has a limited number of decimal places, then YES I can produce a finite number between it and 1, otherwise, you are impressing yourself with being wrong by making a false equivalence.
MM
Again with the unjustified assumptions? How exactly do you KNOW that a rapidly moving observer sees a spherical earth? Have you conducted the experiment? Besides I thought you weren’t contesting the predicted observations of relativity but only the ontological status of these observations. IOW, you agree that the moving observer measures contracted lengths but deny that the phenomenon is real.
In any case, what’s 3 x 0.333333...? Or a different approach, what’s 1 - 0.99999...? That should be a nonzero value if you’re right.
CFT
0.999... is not an infinite number; it’s the sum of an infinite series. By your definition, 1 is also infinite since it equals 1.000.... It too is the sum of an infinite series, just one where most terms are zero.
CFT,
Maybe you could give satisfactory answers: 1/3 = 0.3333... What is 0.3333...x3? What is the value of 1 - 0.9999...?
@Michael Mooney,
I can appreciate what you are trying to learn for yourself, it is quite an undertaking. Just realize that this blog site is most likely not a good place for that. People like dean and Michael have incredible shortcomings... of some undisclosed kind... and find solace in looking for other people to gang up on, make fun of, and look down upon to make themselves feel a wee bit bigger. If they actually knew a fraction of what they wish you to believe they did, they would be far more secure with themselves and be more interested in trying to explain things to you instead of attempting to insult you.
.
If your teacher insults you, it means they can't teach, and you need to find someone else who can.
I take it that you've missed the last 100 or so years.
@Sean T,
spare me your inanity. You aren't even being clever. In case you failed arithmetic, 1 > .999... and .999 < .9999 . All games are played inside of time, including this one. Since in reality (not the timeless symbolic assumption of your infinite series sum over) your calculator or any other computer in existence can't actually produce an infinitely long .999..., (memory is always finite), or locking up in an infinite loop (which is functionally useless), and you most definitely will not live long enough to write it out. Just realize you are conflating an approximation with an equivalence. All I would need to do is find how many decimal places your machine was limited to, or when and where you got tired and stopped writing 9s, and I could then extend the number by one more decimal space, your approximation of an unending decimal number would then be smaller than the number I created. .99 < .999 by .9 ad nauseam, and voila, I could claim victory to having found a number in between 1 and wherever your actual approximation cut off.
.
If you want to get into a numerical pissing contest, try somebody else. I'm extremely not interested.
Narad,
You haven't ever really thought about it, and I can't do that for you. Since you don't care, neither do I.
CFT, the decimal in question is not an infinite number.
Your comment about logical issues is true in some areas, but isn't here. What is at issue is the lack of knowledge mm and CFT demonstrate.
" I'm extremely not interested."
Your comment would be true if you had written "capable".
CFT
What’s the largest possible number then? If you reject the whole concept of infinity, then there must be a largest number. By your logic we cannot actually construct an infinite number oc numbers, hence there must be a largest one. What is it? Once you answer that, then tell me what the value of that number plus one is.
My point is that you do not actually have to enumerate an infinite set to make inferences about that set. The set of all the terms of the sum 9/10+9/100+9/1000+... are such an infinite set. We do not have to actually physically write down all those terms in order to determine that their sum is 1.
Thank you for demonstrating you are like mm and no no understanding of these concepts. It was a safe bet before, it's a certainty now.
I do have to chuckle again at your ignorant blathering about the non-terminating representation of 1 as being an "infinite number". That is a sub-freshman level of inappropriate word use.
#49
"Actually, you are mistaken. .999… is not a finite number, as you indicated with the “…” "
What? I never said it was finite. If it was then this wouldn't work. Obviously if it was finite there would be a number between it and 1. THATS THE WHOLE POINT!! The "..." indicated infinite. Whence there isn't a number between them and thus 0.999....... is the same as 1.
I am sorry but I really don't have the time to write out an infinite number of ......................................................................................................................
and I don't have a key where I can type a 9 with a dot above it, which is the formal writing for an infinite number as I am sure you know.
And yes, I have heard of close but no cigar. Unlike you however, I think that if I get infinitely close I WILL have that cigar.
See what I did there?????? Damn, I'm funny ;-)
No cigar for you, ever.......................................................................................... tired now :-)
Please respond to #52. I'd love to see you try. You may be able to convince me with a coherent argument. You really could.
And while I am at it, would you be willing to accept minus three apples from me in your 'real' world view? MM hasn't responded to that. Please discuss.
"not so smart for someone trying to make someone else look stupid. "
Hmmm. 'Not so smart'. If I take that to its limit then you are calling me stupid.
SEE!!! I did it again. Shame you won't get it.
Cumin now, this is funny!!!
As to making people feel stupid, not at all. Show me where i did that. I am trying to point out errors and fallacies,from my point of view, thats all. Its called discussion. And I have listened to your and MMs point of view on this - i really have. And expressed mine. Or at least sent you a link to a video that I agree with. And the evidence before me makes me simply disagree. Sorry, but I think calculus actually works. If that makes you feel stupid the problem is with you. I never try do that - its unconscionable to me as a scientist, an educator, and a human being. Ask my wife, kids, students, anytime.
I think I see now why scienceblogs is gonna fold. Not much science, more a pissing contest. Thats so sad. Scienceblogs has gone Trump.
I fear for this country - i really do.
My comment at 59 included "and no no understanding ..." when it should have been "and have no understanding ..."
Correction.
I should say 'formal writing for a recurring number'.
"Not much science, more a pissing contest. "
We don't know why it is closing, but to the quote above: Mooney, cft, ragtag, denier, and a few others, have made a habit of stating that any bit of established science they don't like has to be false because -- well, other than the fact that they don't like what it says, they never supply a reason. This part of the discussion shows why for Mooney and cft: neither of them has any command of even the most basic mathematics, but they have the arrogance (good call by Michael Kelsey above) to claim that their takes are correct after repeatedly having the reasons they are wrong pointed out. The people here who have advanced degrees in physics, and those of us who have them in mathematics and statistics, aren't very happy with having people like those two repeatedly claim that their lack of knowledge trumps our experience. Hence the pissing match.
For MM.
Well Michael I tried. Thank you for your comments and links – appreciated. I needed to see what best talked to you.
Waded through some of this stuff, some Ive seen before, much not.
I have a lot of trouble with it all. I am an imaging guy, in Neuroscience. Since day one I have not taken at all to the concept of the brain and the mind being different. Not at all. And certainly that the mind is ‘bigger’ than the brain. With fMRI I can see the brain working, the effects of neurons firing, thinking itself. Right there. It doesn’t happen outside the brain, or in any way separate from the brain.
I havnt come to this in a vacuum. My daughter did philosophy at college and we talked about what she was taught, me in the “this is now bullshit” camp, her in the no its not. We had some great jousts and no doubt will have more. I accept that philosophy was the beginning of us trying to understand, but I still see it as now obsolete – we have a better way and it really works. But that’s just me. And you should also know my wife is a devout catholic – but those are other interesting discussions!!
Very quickly for me this philosophy stuff devolves into hocus pocus ideas of spirit and life and souls and mysticallity. I don’t actually know what life is, but whatever it is I don’t think for a second that there is some magical ingredient beyond the physical that we see. Its just what happens when the stuff the universe is made of gets together under the right conditions. And I don’t like the idea of ‘unobservables’ justified as truths by thinking.
I have seen isolated perfused hearts beating for hours – is it alive?
I have imaged thin pieces of isolated brain, no blood, and watched it activate – seen it ‘thinking’ and responding to stimuli as it would in the brain – is it alive? (Is it ‘conscious’?)
Is a virus alive?
Is a prion alive?
We can take DNA out of one cell and put it in another. While the DNA was outside of the cells was it alive?
An egg cannot divide until hit with a sperm. Before the sperm hit, was the egg alive? And the sperm? OK it cannot exist outside its required environment, but neither can we (and before you say it, we only exist in caustic environments by carrying our non-caustic environment with us).
At no point or at any level do I see a need for anything more than biology and chemistry and physics, and maybe quantum biology. Consciousness to me is an abstract term arising from a sense of specialness.
I do not feel I lose anything with this point of view – its amazing enough as it is for me. And yes I do believe I have free will – that my biology allows me to make choices and decisions - that’s another conversation.
I think anything more is egotistical – our need to be special, like putting the Earth at the center of the universe. It isn’t. And we aren’t. Sorry.
I find ontology and epistemology nonsense, born essentially out of the ideas of religion. Intellectual wordsmithing to try and give spiritual concepts a sense of truth and reality. They aren’t. The idea of justified beliefs I also cannot handle. Can there be justified ghosts?
I don’t like the Euler diagram. It has truth and beliefs overlapping with a common area of ‘true beliefs’. Nonsense to me at least. An abstraction with no reality supporting it.
Some have called it mental masturbation, but that’s just an attempt at an insult. I wont be that shallow. Rather, I may have coined a new term (didn’t show in a quick google) that I think describes my position, and that is that this stuff is ‘mental phrenology’. Pretty catchy huh?
I guess I am, disappointingly for you (maybe), an ‘instrumentalist’. My loss I guess. That term however I find also an attempt at insult, implying that one is narrow minded and missing something.
Show me that something real and we can talk, not things made up in your head.
Rather than instrumentalist, I will stick with the term scientist.
I wonder if I can change my PhD to a SD, since I am clearly not a Ph. ?
As they say (apparently Arthur Sulzberger), I like to keep an open mind, but not so much my brains fall out.
Sorry dude. That’s enough mustard cutting for me. Unless you can show me something ‘beyond’. Show me a ghost, a spirit, an angel, a Leprechaun or whatever. It would change my life of course. As would antimatter particles going ‘upwards’ in a gravitational field. Wow – what a wild thing that would be!!
I expect I will be on your do not reply list now. Fair enough. Have a good life my man and all the best to you.
"I understand the terminology and the history/ ontology of non-Euclidean geometry. Do you? "
Yes. Your assertion that you understand it isn't supported by what you say.
Before I leave this pissing contest on the mathematical concept of the infinite series without reference to real world phenomena... One final challenge: "What is one whole pie?" Is it the same as a pie with an extremely small and ever diminishing slice missing? (No.)
Finally I will clarify the case of the shape of Earth (the actual physical planet) with respect to Lorentz's magical math of physical length contraction.
I have NEVER disputed the *possibility* that an observer approaching at near light speed might see and measure Earth to be flattened in the direction of approach. However, I have ALWAYS claimed that Earth does not change shape with changes in observational frames of reference, and that its shape remains nearly spherical regardless of "how one looks at it." (Physical flattening is impossible.)
Relativity (SR) on the other hand claims that observations/ measurements from all possible (i.e., near lightspeed) frames of reference are "equally valid." Therefore a "pancaked Earth" is an equally valid scientific description.
The latter of course is blatant nonsense still accepted as mainstream science by hardcore true believers in SR. Same as claiming that an a 100 meter train can fit into a 50 meter tunnel because of the differences in measurement between "observer A and observer B"... both (and all) measurements being "equally valid."
I'll leave it there for now.
Ps: When will this blog be closed? I hadn't heard the rumor 'til now. Maybe the folks at ScienceBlogs are tired of science fiction being publicly presented as real science... and tired of Ethan's far out opinions (without evidence) being presented as established facts.
"One final challenge: “What is one whole pie?” Is it the same as a pie with an extremely small and ever diminishing slice missing? (No.)"
And again, your interpretation of the mathematics is completely wrong. The only thing that can be said about your views is that they are consistently, absolutely, false.
@Steve Blackband #65
Just a quickie re: "
"I find ontology and epistemology nonsense, born essentially out of the ideas of religion."
You clearly don't understand either term.
This is just for openers:
http://www-ksl.stanford.edu/kst/what-is-an-ontology.html
"Short answer:
An ontology is a specification of a conceptualization....
As a first approximation, ontology is the study of what there is."
Comment:
What is "spacetime" if any "thing" other than a math/geometry model for gravitational calculation? Is it "really" a malleable medium curved by mass?
Out of time. I'll wing it on epistemology: The study of how we know what we know. It makes the difference between the scientific method and fiction/ fantasy/speculation and opinions formed out of guessing about what we don't know... which pretends to pass for science here at SWAB.
The best back to you.
"The study of how we know what we know. It makes the difference between the scientific method and fiction/ fantasy/speculation and opinions formed out of guessing about what we don’t know… which pretends to pass for science here at SWAB."
I would hate to think that you would ever be in a position of teaching anything -- the damage you would do to the students would take years to erase, if it ever could be.
Hmmmm. Gimme some time to look at that and digest. I appreciate the discourse.
Still not clear at all on your pie description and math only meaningful if it applies to the 'real world'.
Does that mean you won't accept minus three apples from me? What reality does minus three apples have?
And how would you answer #52?
@MM #66,
A. "an observer approaching at near light speed might see and measure Earth to be flattened"
B. "Earth does not change shape with changes in observational frames of reference"
According to your statements, a person standing still on Earth should still measure the Earth to be 'flattened' like the observer in A. measured, because "Earth does not change shape with changes in observational frames of reference"
SB #70: "And how would you answer #52?
Like "sleight of hand" in illusion shows but it would be called "sleight of mind" with "math magic."
Like, "Assume Earth changes shape as various observers see her differently."
No thanks (no apostrophe.)
"Like “sleight of hand” in illusion shows but it would be called “sleight of mind” with “math magic.”"
No, it is basic arithmetic, something available to anyone who puts forward honest thought.
Why do I suspect you are an evolution and vaccine safety denier as well?
MM
So exactly which of these statements is “sleight of hand”?:
1. 1/3 = 0.33333...
2. 3 x 0.3333333... =0.9999...
3. 3 x 1/3 = 1
I will have to assume you find statement 3 non-problematic. If you doubt statement 1, then you must reject the notion that all real numbers have a decimal representation. If you reject statement 2 then what is the correct value of 0.3333... x 3 and how did you obtain it?
One of these three must be rejected since they logically imply that 0.9999... =1.
MM
And you’re still missing the point regarding relativity and the shape of the earth. Relativity does not and cannot say what the true shape is. All it says is that the laws of physics are not observer dependent. The observation of a flattened earth does NOT violate any law if physics. The earth is spherical in our reference frame because the forces shaping it are spherically symmetrical. If that were not the case, the earth would have a different shape.
Now consider the measurements made by a rapidly moving observer. The gravitational force that this observer measures to be acting on a mass element on the surface of the earth will depend on where on the surface it is located. This contrasts with our observation that the force is independent of location. It would therefore be expected from the lawsof physics that elements where the force is higher would be closer to the center than those more weakly attracted. IOW the earth would not be spherical for this observer. A spherical earth for this observer contradicts physical law.
You have stated previously that you do not reject this; a rapidly moving observer will indeed observer a flattened earth. The only question is whether it’s a valid description. Scientifically, all we have to determine this validity is whether or not known physical laws hold. For a moving observer seeing a flat earth, all laws of physics hold. Different values for measured quantities are observed, but the same relationships between these quantities are found to hold for both us and the rapidly moving observer. Scientifically, both descriptions are valid.
You might still have a philosophical objection to treating both as valid. There is no scientific basis for such an objection, though. Our observer would simply mirror your own objection and say the earth cannot be spherical because it’s obviouly pancake shaped, and it cannot change shape. Science gives no way to say whether it is you or the observer who is right.
Back to the *dialogue* (not a pissing match) with Steve Blackband with more time now for some of your other comments.
SB #64: "I guess I am, disappointingly for you (maybe), an ‘instrumentalist’. My loss I guess. That term however I find also an attempt at insult, implying that one is narrow minded and missing something.
Show me that something real and we can talk, not things made up in your head."
The cases of the shrinking Earth and train are two examples. Both are "made up in the heads" of special relativity theorists, based on the *philosophy" that the *real world* depends on how we measure it with our *instruments* and quantify it (in this case) with Lorentz's math... , i.e., it doesn't exist independent of our observations. (A modern variation of the classical philosophy of idealism.)
Obviously (via astronomy and astrophysics) the laws of Nature (described by physics) make all planets and stars some approximation of spherical (mostly oblate spheroids.) They don't change shape (flatten out, etc) as (possibly) seen differently from relativistic frames of reference. Ethan refused to disambiguate the difference between physical and merely apparent length contraction.
And from your #70: "Still not clear at all on your pie description and math only meaningful if it applies to the ‘real world’."
As I said, I assume that the purpose of numbers is to quantify “things in the real world.” ...Being otherwise a meaningless mind game without reference to the real world. The number one is just a number until it signifies something, like one pie. It's not one whole pie if it's missing a slice, however small and diminishing ad infinitum. Those two cases are not the same pie.
Thanks for the respectful (I think) dialogue.
Repeat of quote from link above on the relevance of the philosophy of science:
"... the scientific realist holds that science aims to produce true descriptions of things in the world."
there's more but hopefully that's enough.
Ps: The only meaning I can come up with for your offer to give me -3 apples is that they can not be real apples. Maybe you would be reminding me that I owe you three apples.
"It’s not one whole pie if it’s missing a slice, however small and diminishing ad infinitum. Those two cases are not the same pie."
You are consistent in how you cling to your bad analogies and utter lack of understanding of arithmetic
#72.
Well thats very disappointing.
You are the one insistent on scientific discourse, and I agree with that of course, but in response to #74, which is a very clear, solid and coherent line of reasoning forcing the equivalence of 1 and 0.999........ , (and the word really is equivalence, not same) your coherent, logical and scientifically supported response is that it is 'math magic', or so-called 'slight of mind'.
Not something rational, or a proof, or anything. Just 'it aint so'.
So you have no response.
Your point of view forces you to say that 1/3 is different to 0.3333...... but you cannot tell me why, other than Its magic. Except your 'finite' concept of a pie with a bit cut off it. Infinity is not 'real' to you. By your reasoning the universe thus could not be infinite, which it could be. If I could prove the universe was infinite (which I can't, yet maybe) would infinity then be real to you?
(I can't get my head around a finite universe anyway, cos I get stuck up on whats beyond even though thats apparently not a sensible question to ask).
Using your vernacular, that certainly does NOT cut the mustard.
You have to do better than that. Without something sensible refuting #74, I am forced to dismiss your claim.
I am now hesitant to ask, but given your point of view, what do you make of the weirdness that is the square root of -1 (SQRT-1)? I can't take the SQRT of -1, so much so we give it a letter. Yet I do a Fourier transform every time I take an MRI to get the image, and thus I am forced to accept the reality of a number I cannot express as a number. Its reality is expressed in the ratio of a circle to its diameter. Incidentally it was "Originally coined in the 17th century as a derogatory term and regarded as fictitious or useless".
And what must you make of irrational numbers.
Like 3.14159.......
Which by the way IS the whole pi...... SEE WHAT I DID THERE!! now THATS funny :-)
Followers of Pythagoras could not accept the existence of irrational numbers, and it is said that Hippasus was drowned at sea as a punishment from the gods!
SB #78:
" Infinity is not ‘real’ to you. By your reasoning the universe thus could not be infinite, which it could be. If I could prove the universe was infinite (which I can’t, yet maybe) would infinity then be real to you?"
So, you didn't read my #3 above.
Ethan:
“The answer to the biggest of all questions, of whether the Universe is finite or infinite, might be encoded in the Universe itself, but we can’t access enough of it to know.”
Me:
Reason and logic are still a vital part of the epistemology of what we know and how we know it.
If one claims that the universe is “possibly” finite, one must explain/define the “possible” boundary… what it IS… and then what lies beyond that imaginary boundary…. What else but more space with more stuff in it, ad infinitum?
"Your point of view forces you to say that 1/3 is different to 0.3333 "
Sure it's different. Numbers must have reference to whatever they are quantifying *in the world.* A third of my pie is quite a clear reference. Two thirds of it are gone. An infinite series of threes after a decimal does not describe a fraction of a pie or anything else in the world. It's never complete. It's a mental concept without reference to anything.
And, speaking of Pi (!), we all know that there is no end to the decimals after the three, but it does express the ratio between a circle's diameter and circumference as best a string of numbers can... the longer the string the more precise the ratio. So it's just a math question beyond absolute and complete quantification: "How many diameters does it take to go around a circle?" But when you slice a pie in half, the question is not relevant unless you also cut off the crust all around the edge and wonder how much more cutting that requires. (About 3.14 times as much.)
I'm throwing in the towel on the infinite series of .999s equaling 1 (but "not the same as" 1!) I'm still not a mathematician, nor do mathematicians consider the "reality" of the "real world" questions I pose, like "one what?" or "what is the difference between a very large and increasing part (not quite a whole) and the whole?"
Yea lets stop.
I can't make you see there is nothing between 0.999.... and 1.
You can't show me that there is anything between them.
You run counter to any textbook, scientist, mathematician I have ever met, and calculus, and miss out on so so much that is closed off to you. Your position doesn't produce any useful results.
C'est la vie, and good luck with that.
SB,
I have "run counter" to all kinds of indoctrination my whole life (now 72.) I'm not about to quit it now.
I'm not sorry to have disappointed you for not swallowing the "infinite series" math concept as a real quantification of things in the real world.
Same lack of remorse for not answering your "spiritual" challenges. This is *supposed to be* a science blog and science doesn't yet include personal testimony about such experiences.
I do recommend a deep study of David Bohm's life work as a mystic as well as a quantum physicist. His implicate order is the best work yet, in my opinion, by a scientist trying to explain the nature of an omnipresent "field" by whatever name. Looks like "IT" will not be named after Higgs after all.
How did that happen? You're cheerleader for Zeno, after all.
@MM #81: Since you don't believe in infinite series, I can guess that you must believe that the accurate targeting of Japanese ships by the U.S. Navy in the battle of Midway was all a hoax, along with every other artillery battle since the 17th Century. Also, presumably you reject the notion that we can compute the area of a circle, or the volume of a sphere. Does "pi" equal three in your reality?
"I’m not sorry to have disappointed you for not swallowing the “infinite series” math concept as a real quantification of things in the real world."
Except they are real world quantities. They are the basis for myriads of calculations throughout mathematics, physics, and other applied areas. There is no "philosophical issue" with the underlying mathematics, as you and cft continue to claim. Much of this was sorted out with the rigorization of analysis in the 19th century. As Michael Kelsey, I, and others have pointed out: you can't have it both ways: you can't claim these issues of (really) fundamental calculus are bogus and then accept the results they provide -- at least, not without coming off as failing to understand the ideas.
Get over the "stopping point" argument about the non-terminating decimal of 9s.
"You run counter to any textbook, scientist, mathematician I have ever met"
Yes he does, and seemingly doesn't realize this contradiction: he repeatedly claims they aren't real, that only things like '1' is real -- but he can't show you a 1 either, only something that is a representation of the idea of 1.
MK #38
Well, that was nasty and insulting.
I don't "believe in" anything, as a scientist. Belief contaminates objectivity.
No I don't believe that battle victory was a hoax.
DON'T PUT WORDS IN MY MOUTH! I hate that!
No, I don't "reject the notion that we can compute the area of a circle." Too much "presumption." It's obvious (Pi X radius squared.)
Aside:
We can pour out the liquid volume of a sphere into a measured container and forget about computing. (Just another reality check.)
This will be my last reply to you, because you are obviously not here for anything close to respectful dialogue about science.
As a psychologist I recognize your "will to power" and obsession with dominating others. I've had enough of it.
Open your mind. Your brain will not fall out!
Enough!!
Edit: I meant to say #83. I wish I were not dyslexic. I wish for honesty in science too. Not that optomistic!
What do infinite and eternal mean in cosmology? (This may be off topic but who cares?)
Question your assumptions. Look for evidence. Maybe the universe is not expanding at an accelerating rate. This link is about two years old. (Old science.)
https://www.nextbigfuture.com/2016/10/accelerating-universe-expansion.h…
"... the researchers have found that the evidence for acceleration may be flimsier than previously thought, with the data being consistent with a constant rate of expansion."
Don't jump to conclusions about an oscillating universe just yet. We can't measure such a cosmic two phase cycle.
But of course "reality" is confined to our ability to "measure."
I'm pretty sure that is Ethan's BELIEF.
Most of the speculation about dark matter and dark energy are based on assumptions (guesses) about the realm of what we do not know (Ref: Epistemology) yet given names as if they were actual entities.
Both "DM and DE" are examples of "unobtanium!" (An old joke revived here by CFT.)
Let's distinguish mind games from the scientific method. Just a few last words. I'll be gone when Ethan's product becomes a commodity for sale.
(I'm posting comments too quickly, says the prompt. I'll wait.)
"as a scientist."
You are many things, but scientist is not among them.
So, wait, MM has just proclaimed himself both a scientist and a psychologist? I imagine that the esteemed Thunderwood College would have nothing of this.
As per #89 and #90, personal attack/ harassment of all critics of "mainstream science" remains the general tone here, as set and continually demonstrated by Ethan. The absence of this blog will be no loss to the scientific community.
You jerks clearly don't know that science is not an exclusive club for those with credentials proving their indoctrination by the present/ contemporary mainstream as taught in academia. It's not all about crunching numbers, as the elite club of mathematicians want to believe.
I'm sure everyone will be awaiting your first vixra preprint with bated breath.
@MM #91:
"It’s not all about crunching numbers"
I think that is actually correct, at least for physics.
I think most people think physics is all about math (today).
But I had read somewhere Einstein actually made his discoveries w/o math and left the math explanations to others. He actually had hard time learning advanced math (probably for all his life).
But still his ideas clearly made sense when expressed with math later. So it still does not mean any idea about physics would still work when it converted to math.
MM,
I agree with you; math and physics are two separate studies. Yet, it is people like CFT and you who are the ones conflating them. Math has NOTHING to do with the real world. A mathematical system is simply a set of assumptions, referred to as axioms, that are taken as the starting point for the system. The system then consists of these axioms plus whatever other statements can be logically deduced from them.
There is nothing in this requiring that these axioms must be related to the real world in any way. We can certainly do mathematics based on ANY axioms, subject only to the condition that the axioms are not self-contradictory (this exists only because it's logically possible to deduce any statement from a set of contradictory axioms; that would be a useless mathematical system). Mathematicians can and have discussed the geometry of N dimensional spaces, where N >3 (in some cases much greater), they can discuss geometries limited to the surface of a torus, sphere, or any other shape you can imagine. We can discuss systems where 1+1=1, and we can discuss systems where a donut and a coffee cup have identical shapes. It all depends on the starting axioms.
Of course, some such systems are more useful than others when it comes to dealing with the real world. That's where physics and the other sciences come in. Science determines which of the sets of possible axioms are the ones that best describe the real world. Once we come up with such a set, usually called physical laws, we can then use the known mathematics based on that set to make conclusions about the real world.
Your arguments regarding the equivalence of 0.99999... (infinitely repeating) and 1 are entirely unfounded. Given the axioms used to construct the system we call "real numbers", these two values are indeed equal. Any arguments I or anyone else gave are really irrelevant. They are equal based on the axioms of the real numbers. There are axiomatic systems, such as the surreals, where they in fact are not equal. This system allows for so-called infinitismal quantites, one example of which is the value 1 - 0.99999.... These are quantities that do not obey the Archimedian property of real numbers. If you are unaware, this is a theorem in real numbers that does not hold for surreals. Namely, given any two numbers a and b, with ab.
I don't mean to go completely off topic, but I just wanted to show the point that the math is inarguable. The consequences of the axioms are what they are. There is no room for opinion on the matter. The real numbers are DEFINED in such a way that 0.9999.... = 1, and that's pretty much the end of it. Your arguments are limiting the real numbers strictly to the concept of Turing computability, i.e. the only permissible numbers are ones that can be reached via a finite computational algorithm. That would in fact exclude the value of pi, which is why it was brought up. You can't have it both ways; you cannot say that the area of a circle is pi x radius, but deny that 0.9999... = 1. Both pi and 0.99999... are the sums of infinite series; logically you cannot reject one and accept the other.
I think my above a particular line was misinterpreted as an HTML code. I meant to state the Archimedian property of reals which is that given two reals x y. I originally used "b" as a variable and it interpreted that as a "bold" tag.
Still not rendering! Drat! Well, not that important anyway. Basically, the property of reals is that no matter how much smaller one real number x is than y, we can always find a value z such that xz is greater than y. That is not the case with infinitismal quantities that are permitted in the surreals.
@Sean T #95: "Math has NOTHING to do with the real world."
WOW! Even I wouldn't go that far to deny the relevance of math. Most of us use numbers a lot to quantify real things. ("I'd like five pounds of roast beef, please"... or How far is it to Andromeda in light years and fractions thereof?)
I did a lot of calculation as a masonry contractor too. Not so much as a psychologist except for my B.S. in behavioral psychology... learning theory, running rats through mazes.
Never much used algebra since my high school classes 56 years ago. ... But I'm rambling.
My objection is to the abuse of math-as-reality without a referent in the real world... standard procedure for many, like Ethan.
A coffee cup is topologically a torus whether one likes it or not.
(teletype sounds...} This just in...internet commenter finds comment sections available to spread their lack of knowledge dwindling at an alarming rate...fear no one left to drive away from actual discourse on the internet...report at 11:00....(teletype sounds....}
I am NOT denying that math is useful in the real world. I am merely pointing out that the validity of a mathematical system is independent of any feature of the real world. A mathematical system can be a perfectly valid one regardless of whether or not it corresponds to anything in the real world. The mathematical system is an entirely self-contained system. The only requirement for a valid system is that the starting axioms must not contain contradictions.
Of course, in the real world, we do find math useful. Undoubtedly, the historical development of math had quite a bit to do with the real world. The first mathematical systems developed were ones whose axioms appeared to the developer to be self-evident, i.e. they corresponded to the real world. That's the true origin of Euclidean geometry. Euclid did not choose axioms randomly; he chose ones that appeared to hold when he actually drew lines, circles, etc.
I am certainly not denying the relevance of math to the study of the universe. Like I said in my full post above, the job of science is to find out which of the possible mathematical systems best matches the real world. Having done so, these systems can then be used to make further predictions about the universe. If these predictions continue to hold true, we gain confidence that our chosen mathematics is useful. If not, we modify the mathematical system we use to describe the world. Far from irrelevant, mathematics is quite relevant as a tool for making predictions.
Ah, you guys are still chewing on this one. At the root of the entire problem is the evasion of a simple underlying truth: you can't incrementally approach infinity, its a paradox, you can move in its direction, but you are no closer than when you started. When you 'sum over', you are just hand waving away something you can't actually do except in your imagination.
.
@Sean T #95,
You can talk about infinite numbers, but you actually can't have one (as they aren't fixed static values and you don't have forever to write it out) except by symbolic representation (your imagination), or calculate them, except by approximation. All math abstraction still requires 'real' time to be considered and performed, there are no exceptions, unless you claim you can perform abstract logical operations that don't require some time to perform, which is absurd. The beauty of 'Turing computability' as you put it, is that is forces one to realize the useful limitations of what you are actually able to compute. Computability is where the rubber meets the road in all calculation, you find out if your mental abstraction is actually doable in a finite amount of time. If a calculation requires infinite steps or time to perform, it really isn't a calculation anymore than a man pushing against an unmoving boulder is doing work, it isn't going anywhere. A prediction that takes forever isn't a prediction.
.
Calculation:
a mathematical determination of the size or number of something.
"finding ways of saving money involves complicated calculations"
.
synonyms: computation, reckoning, adding up, counting up, working out, figuring, totaling up, totting up
"the calculation of the overall cost"
.
•an assessment of the risks, possibilities, or effects of a situation or course of action.
"decisions are shaped by political calculations"
synonyms: assessment, judgment;
.
To do anything with a calculation such as make a determination (which is what math is for) you have to be able to accomplish it.
.
As to your statement, "the area of a circle is pi x radius", it actually isn't, this is why the Greeks were uneasy about Pi, anything you do with pi is only an approximation (you can't actually use all of Pi). To this day mathematicians keep trying to calculate more digits of Pi, to get a greater amount of accuracy with the approximation in calculation.
CFT,
Go ahead and keep on with your incorrect notions; they are still incorrect. The requirement you are discussing is called Turing computability. Mathematics most certainly does NOT require Turing computability for any of its conclusions. It is true; you cannot determine the value of an infinite sum by actually adding all of the terms; that would be absurd. Fortunately, the axioms of mathematics permit the determination of such sums by means other than direct calculation. Contrary to your assertion, calculation is most assuredly NOT what mathematics is for. (In fact, actual mathematicians very rarely actually calculate anything; many are quite bad at doing such calculations)
Just a simple example: suppose you have a value a that is strictly between zero and one (i.e. it cannot be equal to either one or zero). You wish to determine the infinite
sum 1+a+a^2+a^3.... We start by considering the FINITE sum (which I assume you would have no problem with) 1+a+a^2+a^3+...+a^n. Let's call this value s. Now consider the value as = a+a^2+a^3+...+a^n+a^n+1. Now the value of s-as = 1-a^n+1 (all other powers of a are cancelled in the subtraction). Therefore, s(1-a) = 1- a^n+1 and thus the sum is s = (1 - a^n+1)/(1-a).
So far so good, and I am sure that you have no issue with the above since it can be directly checked by finite calculation. However, the axioms of the real number system allow us to consider what happens when n becomes infinite. When that occurs, the term a^n+1 becomes zero since a is strictly less than one. Therefore, the infinite sum is equal to (1-a)^-1. For some numerical examples, the infinite sum of powers of 1/2 (zero to infinity) is 2. For 1/3 it is 3/2. For 1/5 it is 5/4 and so on.
Whether you accept or deny this conclusion is really not relevant. The axioms of the real number system combined with the logical rules of inference GUARANTEE that this conclusion is correct, at least within the realm of the mathematical system of real numbers. Whether or not the mathematical system of real numbers is a useful description of the actual universe is an entirely independent question. Obviously, most of us would answer that this mathematical system is indeed quite useful, but that is really irrelevant to the conclusion that the infinite power series is convergent for any a in the interval (0,1) and its sum is (1-a)^-1.
You're still going to die someday, Zeno.
CFT,
BTW, mathematicians continue to calculate more and more digits of pi simply because of curiosity and because of certain conjectures regarding the randomness of those digits. The value of pi is known to a far greater degree of precision than is even theoretically possibly required in any real world measurement. We literally know millions (if not more) digits of pi. We can certainly never even hope to use more than 30-40 or so of those before running into the inherent uncertainty of measurements in nature. The accuracy of measurements and calculations involving pi has nothing whatsoever to do with the continued calculation of further digits.
@CFT:
You seem to overlook computers also do symbolic calculations, which can handle calculations using full exact value of pi, e etc.
I hope you will not claim symbolic calculations are not mathematically valid calculations :-)