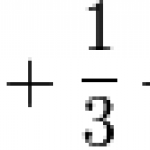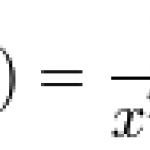Sunday Function
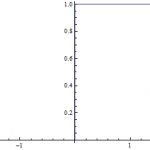
mspringer | February 15, 2009On the surface it's one of the most boring possible functions. Two straight horizontal lines: the Heaviside step function.
Usually denoted θ(x), it's equal to 0 if x is less than zero, and it's equal to one if x is greater than zero. At x = 0 exactly it doesn't really matter what it is for physics purposes so it's generally taken to be 1. Mathematicians tend to define it as 0.5 at x = 0, but they're kind of weird.
Believe it or not, there's some pretty good reasons for having the Heaviside function around. Walk into a dark room and flip on the lights. Before you hit the switch, the…
mspringer | February 8, 2009Continuing my series of basic concepts with middle school math will be tricky when we're doing a Sunday Function. But let's give it a shot, and see if we can keep it to that beginning level.
This function is pretty simple. You add reciprocals until you get reach whatever number n you've picked, then you stop. Formally the function has a name - the harmonic series. As you pick bigger and bigger n, the sum will be bigger and bigger. There's no limit to how big it will get, but clearly its growth will be pretty slow. If you want f(n) = 100, n is going to have to be pretty stinking huge.…
mspringer | February 1, 2009First, a very quick and simple introduction to recursion. Here's an example. Pick a positive whole number n. The factorial function in the product of all the integers between 1 and n. For some reason it's denoted by an exclamation point.
Now if you compute 5!, you don't need to repeat the whole process if you want to compute 6!. You can just take the answer to 5! and multiply that by 6. Explicitly, because 5! = 1x2x3x4x5, that means 6! = 1x2x3x4x5x6 = (1x2x3x4x5)x6 = (5!)x6. Let me write this generally:
Now just keep that in the back of your mind for a moment and let me show you a…
mspringer | January 25, 2009There's some math here, I'd rate it at Calc 2 difficulty. If you don't know calculus, that's fine! The details will be obscure but I think you'll still appreciate the abstract beauty of the method.
Ok, pick a rapidly oscillating function. It doesn't really matter which, so as an example I'll make one up. It has no particular physical significance, but the method we're going to test out on it ends up being very useful in numerous physical problems. A lot of things oscillate, and many times we're after the overall average effect of those vibrations, not the details of the vibration itself…
mspringer | January 18, 2009One of the most important mathematical concepts in physics and pure mathematics is continuity. There's a formal definition for it which for the moment isn't too relevant, but for our purposes we can think of it in terms of smoothness. Put your finger at a point on the graph, and if the function smoothly approaches from all directions with no instantaneous jumps or gaps and it's continuous at that point. But it can get kind of tricky. Here's one that's frequently presented in intro multivariable calculus classes (I first encountered it on page 904 of Stewart).
Its mug shot:
Ignore the…
mspringer | December 28, 2008Here's this week's Sunday Function. In the universe of functions it's an utterly typical suburban middle class citizen, with a pleasant but quite ordinary job in a downtown cubicle farm for Physics Incorporated.
His name is.
In a little more detail, you'll notice that this function is the product of two elementary functions. There's x squared, and there's e raised to the negative x power. As x increases, obviously x squared increases quite quickly. By the time you get to x = 500, x squared is equal to 250,000. But on the other hand, e^-x is shrinking as x increases. It happens to be…
mspringer | December 14, 2008The Exponential Function. I think this is the first time we've done it here. It won't be the last. You could write a book about it, and someone probably has. Here's the usual picture:
This graph isn't as pretty as the usual, because I'm at home with my old copy of Mathematica 5 instead of the new version that's much better at drawing smooth and professionally-colored graphs. Nonetheless, the essential details are made clear. The exponential function drops off to zero very rapidly as you go left, and increases rapidly as you go right.
You can define the exponential function in any of…
mspringer | December 7, 2008This rather striking image is the imaginary part of the Airy function. Rather than a lot of words today, I'd like to just present this mathematical function as art.
I've always disagreed with Whitman in his assessment of science, but it is nonetheless a good thing to occasionally look up in silence at the stars - or function plots.
WHEN I heard the learn'd astronomer;
When the proofs, the figures, were ranged in columns before me;
When I was shown the charts and the diagrams, to add, divide, and measure them;
When I, sitting, heard the astronomer, where he lectured with much applause in the…
mspringer | November 23, 2008This function is a two-dimensional one. It's radially symmetric however, so we can specify it with only one coordinate - the distance from the origin r. It's the two-dimensional Gaussian function, and it looks like this:
As r increases, -r^2 very quickly becomes a large negative number. The exponential function falls off rapidly toward zero at negative arguments, and so as you move away from the origin the value of the function is pretty much nil.
Now if you think of that graph as a clay sculpture, you'll see that almost all of your clay will go to making that central bulge. Away from…
mspringer | November 16, 2008Here's sin(x).
What, you don't believe me? Ok, ok, I'm leaving something out. Let's do some background before I tell you what it is.
The first thing we need is the incredibly interesting and important Euler's formula. It's the key that relates the exponential and trigonometric functions. We won't pause to figure out why it's true, for now we'll just take it as a given:
Now replace x with -x, and we'll use the fact that cos(x) is the same as cos(-x), and sin(-x) is the same as -sin(x).
So that's two ways of saying the same thing. Now we'll subtract the second equation from the first.…
mspringer | November 9, 2008Math-averse readers! Do not be scared off! You can enjoy this entry even if as far as you're concerned the equations are pretty pictures of Cypriot syllabary.
Not long ago we looked at adding up lots of consecutive integers. Multiplying consecutive integers is also interesting, and not only that it has a tremendous number of uses all throughout physics and pure mathematics. The function that multiplies the integers from 1 to n is called the factorial function, and rather unusually it's denoted with an exclamation point, like this:
Here I'm using dots to denote multiplication, as is…
mspringer | November 2, 2008You know about the tangent function, tan(x). If you draw a right triangle, the tangent is the ratio of the two sides which comprise the right angle. If the angle between the long sides and each of the short sides is 45 degrees, then clearly the two short sides have the same length. That means the tangent of 45 degrees is 1.
Now the tangent function has an inverse, which we call the arctangent. It's our Sunday Function, and it looks like this:
In mathematics we never use degrees as a measurement of angle, we use radians. There's 2π radians per 360 degrees, and so a 45 degree angle is…
mspringer | October 19, 2008Time for a vacation! Grab a globe of the earth and pick a random number between 0 and 180 degrees for your latitude and between 0 and 360 for your longitude and set off on your vacation. It's exciting! You're bound for anywhere on earth, and every obscure location has the same probability of being chosen!
"Not so fast," the stern voice of vector calculus intones. "In fact not every location is equally probable. You're most likely to be visiting one of the polar regions if you pick a location using your method."
Why is this? Picture abstractly a globe of the earth with a latidude and…
mspringer | October 12, 2008Quick! Add up all the numbers between 1 and one trillion, inclusive!
The story goes that the great Carl Friedrich Gauss in his days as a little kid in late-18th-century German primary school was told with the rest of his class to add up the numbers from one to one hundred. The teacher was probably tired of the little squirts and wanted to keep them busy for a while. Gauss is in solid contention for the title of Smartest Man Who Ever Lived, so it took him a few seconds. Not because he was a arithmetic savant - most mathematicians are not unusually good with actual numbers - but because he…
mspringer | October 5, 2008As we get closer to Halloween, let's take a look at one of the few functions that might cause a stir in Salem. I give you the Witch of Agnesi, for several values of its free parameter a:
The Witch is a geometric construction involving triangles that's easier to show than describe:
(Both images are from the Wikipedia article)
Geometric construction though it is, you can also write it in closed form as a standard old function of x:
Why did this seemingly mundane function merit such a creepy name? It was originally named by the Italian mathematician Maria Gaetana Agnesi, who called it la…
mspringer | September 27, 2008Due to some homework which is taking longer than anticipated, today's Sunday Function will have to be a bit quick. It's no less interesting for that.
Define a function Q(n) on the natural numbers, such that Q(n) = 1 for a prime number and Q(n) = 0 for a composite number. In other words, it's just a function that checks to see if a number is prime or not. If you were trying to evaluate this function by hand, you could do so by manually dividing n by all the numbers less than n to see if anything divided evenly. Actually this would be very inefficient, you only have to divide by the prime…
mspringer | September 21, 2008In our tour of the zoo of functions we've been spending time in the snake pit. These are the pathological functions of pure math, and are generally but not always useless in physics and pretty much everything else. But they're very cool to look at! We'll eventually get back to the useful domesticated farm animals of the functions but we're in no hurry. Here's the next snake and its picture:
It looks like a double-valued function, a straight line under a parabola. but it's not. If x is rational, f(x) is just the square of x. Otherwise, it's 0. So f(π) = 0, but f(3) = 9.
It's loosely…
mspringer | September 14, 2008Draw the graph of a function. Roughly speaking, if there's no holes, jumps, or other choppy weirdness it's a continuous function. The function is connected to itself like a curvy rope laid out on the ground, with no cuts.
Now if that function has no sharp points, it's a differentiable function. Again roughly speaking, imagine that the rope is free of kinks or sharp bends. The absolute value function is an example of a function which is not differentiable at the origin: there's a sharp point there.
It's well known that if a function is differentiable, it's also continuous. This is…
mspringer | September 7, 2008Take as our starting point this function, defined on the positive whole numbers:
All it does is add together the fractions above, stopping when you hit the fraction specified by your particular choice of n. As you increase n and thus add more fractions to the sum, you'll end up with a plot of the function that looks like this:
As you keep adding more and more fractions the sum will get larger and larger, but the rate of growth will be very slow. I've stopped plotting at n = 100, where the last fraction is of course 1/10000. But even though the growth rate keeps slowing down, how do I…
mspringer | August 31, 2008We can't graph here, this is bat country! Complex bat country.
...well ok, let's stop and take a look anyway. But no graph.
You've seen this jewel of mathematics. It's Euler's identity.
It comes from the more general expression right below this paragraph, which is today's Sunday Function. You might wonder where this expression comes from. It's a long story, but if you want to plow through it, I commend you.
Set θ = π, and Euler's identity pops right out. But let's set θ = π/2 instead and see what happens:
In other words, we've just figured out a new way to write the imaginary number…