Might as well jump. Jump. Go ahead, jump. - Van Halen
Suppose everyone in the world got together and jumped. Would the Earth move? Yes. Would it be noticeable? Time for a calculation. Note: I am almost certain that I have done this before, but I can't find where.
Starting assumptions.
- 7 billion people.
- Average weight: 50 kg (you know, kids and stuff)
- Average vertical jump (center of mass): 0.3 meters - and I think that is generous.
- Mass of the Earth: 6 x 1024 kg
- Gravitational field near the surface of the Earth is constant with a magnitude of 9.8 N/kg
- Ignore the interaction with the Sun and Moon
Basic physics
Suppose I take the Earth and the people as my system. In this case, there are essentially no external forces on the system (see assumptions above). There will be two conserved quantities - momentum and energy. Here, the term conserved means that that quantity does not change. I can write:
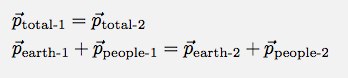
What does the "1" and "2" mean? These could be any two times. For this situation, let me say that time 1 is right after the people jump (and still moving up) and time 2 is when the people are at their highest point.
Energy is also conserved. If I take the people plus the Earth as the system, then I can have both kinetic energy (K) and gravitational potential energy (Ug). Using the 1 to represent the people just jumping and 2 to represent them at their highest point, then:
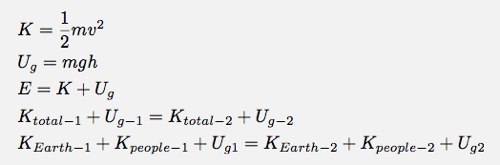
About gravitational potential. First, it is the potential energy of the system, not of each object. Second, in this approximate linear form (mgh), the change is what really matters. This means that I can set the potential at point 1 as 0 Joules. Also, the mass of the Earth does matter in this potential - that is where the 9.8 N/kg comes from.
The calculation
A couple of important things to start with. At position (and time) number 1, the Earth and the people are moving but there is zero gravitational potential energy. At position 2, the Earth and the people are 0.3 meters apart and not moving (at the highest point). Finally, momentum is a vector - but this is a one-dimensional problem. I am going to let the y-direction be in the direction the people jump.
This gives a momentum conservation equation of:
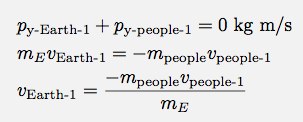
Now, I can use the energy equation to get an expression for the initial velocity of the people:
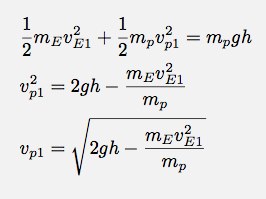
Just a quick check with reality. If you want to jump a height h, you would need a speed of:
![]()
This is what you get if you assume the velocity of the Earth is super small from above. Ok, I am going to put these two equations (momentum and energy) together. This looks bad, but it really isn't too bad. The problem is the velocity of the people from the work-energy method still has the velocity of the Earth. Avert your eyes if you are algebra-allergic.
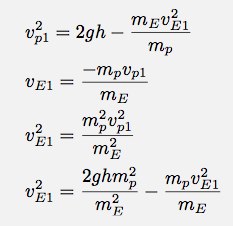
Not finished quite yet - I need to now solve for the velocity of the Earth.
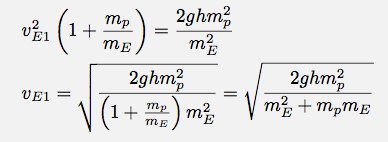
See, that wasn't too bad. You can open your eyes now. Now for the numbers. If I use the values form above, I get a recoil speed of the Earth as:
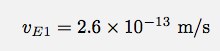
Maybe you don't like my starting values. But you know what? It doesn't really matter - the mass of the Earth is so huge that it is going to be pretty darn difficult to get a detectable speed. Also, there is the whole issue of getting everyone at the same place at the same time and getting them to jump at the same time.
I seem to recall the last time I did this calculation (that I can't find) that I also estimated how many people you could get in one spot of the Earth.

How about a different but related question.
What if the word goes out that everyone in the world is going to do the jump experiment. A suitable spot is chosen and on a certain day (...might as well make it a certain week; the logistics would be awful) every person on earth shows up and stands/sits/mills around for a while waiting for the jump experiment to begin.
How would this change in the distribution of the mass of people affect the moment of inertia of the earth, and in turn affect its rotation?
(Did you see what I did there? "In turn"? That's gold right there.)
Angular momentum L = I w is constant. I goes from (I_1 = I_earth + I_p1) to (I_2 = I_earth + I_p2) where I_p1 is with people distributed evenly about the earth's surface and I_p2 is all people concentrated at some spot on earth. The initial angular speed w_1 is 2 pi radians / day, and I'll let w_2 = w_1 + dw where dw is some small change in the angular speed.
Conservation of angular momentum tells us
(I_earth + I_p1) w_1 = (I_earth + I_p2) w_2 = (I_earth + I_p2) w_1 + (I_earth + I_p2) dw
So, solving for dw gives us
dw = (I_p1 - I_p2) w_1 / (I_earth + I_p2)
Now we have to put in all those moments of inertia.
I_earth = 2/5 m_E (r_E)^2
I_p1 = 2/3 m_p (r_E)^2
I_p2 = m_p (r_E)^2
Leaving us with
dw = -1/3 w_1 / ( 2/5 m_E + m_p) = -1.39 x 10^(-25) w_1
In other words, putting all the people on earth in one spot would shift the length of the day by many orders of magnitude less than a femtosecond.
It seems that the location of the people on earth would matter. Wouldn't people "across" from each other cancel out? Thus, for this exercise some people's jumping would weigh more than others. That said, it appears it would not matter compared to the size of the earth which is reassuringly large.
Great blog, thanks!
Thanks for reminding me once again that there are people out there who can do all that maths so I don't have to. *salutes*
Quick question: the people all fall back to earth because of the earth's gravity. Does the earth also fall back to the people? If so, does this then cancel out the amount that it moved in the first place?
Would the overall obesity of Americans cancel out the thrice-as-many Chinese (since we all know that China is directly across from the U.S., as evidenced by all our childhood attempts to dig a hole to China)?
@theshortearedowl,
Yes, when the people fall back down the Earth would move back up. It would cancel out the displacement of the Earth, but not the motion (there and back).
@James,
I think 50 kg is a nice average mass - but even if you doubled the mass of the entire human race, it would still be a super small velocity of the Earth.
I want to see Mythbusters put this one to the test.
When I saw the title, I was expecting something a bit different--same question, but for the passengers on a large passenger plane. (I have heard stories of the Stanford marching band members all moving from one side of the plane to the other at once--I suppose they could volunteer to do the jumping experiment as well.)
Many years ago (early-mid 80s, I think) the Weekly World News ran a story about how the Chinese were planning such a coordinated jump, in order to knock the Earth out of orbit. Therefore, patriotic Americans needed to organize a counter-jump in order to save the planet!
Ok, but riddle me this batman, what if everyone on the earth faced in the same direction and simultaneously farted? Would it alter the speed of rotation?
There's a big issue with assuming that energy is conserved. While this is technically true, a huge amount of energy would be wasted in the form of heat. Thus you cannot simply equate the total kinetic and potential energy at the beginning and the end. For each person to jump they expel some heat and that's not mentioned.
It *wasn't* everyone on the planet but I believe it was still a decent amount of people; this was done back in 2006:
http://www.worldjumpday.org/
http://en.wikipedia.org/wiki/World_Jump_Day
Would it be possible to change the length of the day if everyone on the earth was to run in either east or west? It sounds easier than making everyone jump in the exact same spot..
Hi guys, just wanted to let you know that The Energy of Word, an international media competition aimed at journalists writing about energy issues, will start accepting applications in February 2012. Please spread the word: http://www.globalenergyprize.org/en/request/pen/new