One of the underappreciated aspects of chess composition is that some problems have a sense of humor. Sure, the real classics show deep and surprising ideas and do so with impressive constructional finesse. But other problems just bring a smile to your face. This week I have two such problems for you. Neither is difficult to solve. In fact, they are both trivial to solve. But both made me smile when I saw them, and that makes them good problems in my book!
Last week I reported on The US Amateur Team East chess tournament. One of the great joys of this tournament is the chess bookstore run by Fred Wilson. Fred has a chess store in New York City, which I heartily recommend you visit if you're in town and like chess. He had a number of rare books on chess composition on hand at the tournament, and I mostly cleaned him out. Alas, most of them are not in English, but chess is a universal language!
One was a small paperback in German called Chess Curiosities. It was authored by Karl Fabel, a composer who specialized in such things. So, without any further ado, here's the first problem. It was composed by Fabel and Sontag in 1956. The stipulation calls for Selfmate in Five:

Recall that in a selfmate, white plays first and forces black to give checkmate in no more than the stipulated number of moves. Black, for his part, will do everything in his power to avoid giving mate. It is a complete inversion of normal chess logic!
You have probably already found the solution. White must escort the black pawn down to b2, which he does with some aesthetic knight hops: 1. Nf6 gxf6 2. Ne5 fxe5
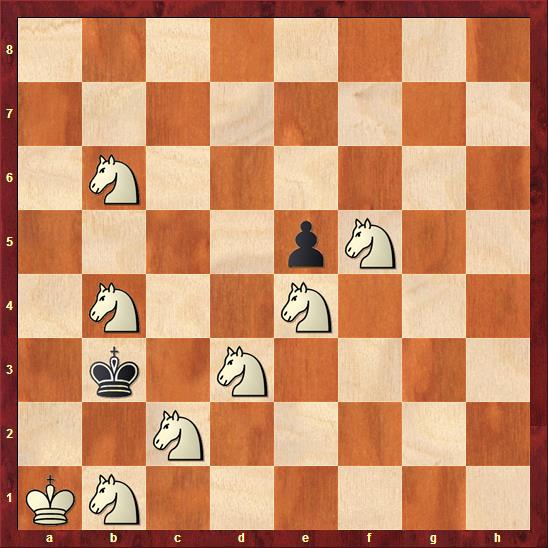
3. Nd4 exd4 4. Nc3 dxc3 5. Nb2 cxb2 mate.
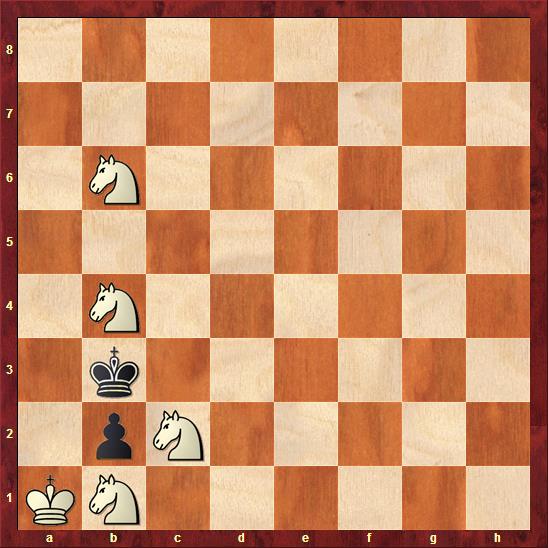
Like I said, very simple but undeniably fun!
The theme of clever knight arrangements continues in our next problem. It was composed by P. H. Williams, but the book does not give the year of publication. White is to play and mate in two:
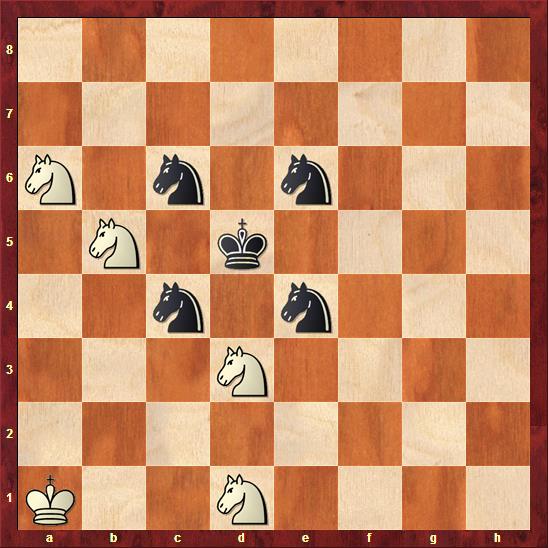
A quick scan reveals that white is prepared to deal with any hop of the black knights. Such a move by black would give the black king a flight square, but it will also unguard a square from which one of the white knights (from a6 or d1) will give mate. The white knight will not only give check, but will also cover the newly opened flight square.
The trouble is that white needs a waiting move. It is plain that he cannot move any of his four knights without messing up the set play, which leaves the king. Any king move will leave him exposed to a check, however, so white must choose carefully.
The only move that works is 1. Ka2!:

Now a typical line is 1. ... Nf8 2. Nc7 mate:

The other variations are similar, so I will leave them as an exercise to the reader.
Good stuff! See you next week.

I must say, my first thought on scrolling down to the first diagram was that my computer monitor was having an image-repeat fit.
Next, I was delighted to see that these are actually SOLVABLE by a reasonably normal chessplaying human being.
Third, for some reason these chess problems reminded me of the oriental board game, Go. (Which I have never quite gotten the hang of....)
So thanks again for posting these problems. Oh, by the way, you were certainly correct about the Nunn Chess Puzzle book being more than a bit challenging. Hard work.
I wonder if the first position is possible. I mean, obviously you can promote up to 8 pawns to knights, but I am skeptical you could manage to reach the position there without stalemating. Regression analysis, perhaps.
Yes, the first position is possible. I just constructed a (very boring and stupid) game leading to it; it happened to take exactly 100 moves to reach that position. The last moves were ... Ka4; Nd7-b6+ Kb3. I didn't have to do anything very clever on the way, other than making sure White promoted enough pawns to knights and Black didn't move his g-pawn.