Few-Body Systems: Cooler Than You Might Think

Hey, dude? Yeah, what's up?

I'm not normally the one who initiates this, but I was wondering: When you were at DAMOP last week, did you see any really neat physics? Oh, sure, tons of stuff. It was a little thinner than some past meetings-- a lot of the Usual Suspects didn't make the trip-- but there were some really good reports from a lot of groups.

Anything really surprising? Well, there was one talk that I really liked a lot, that I went to on a lark, because I didn't understand what the session title could possibly mean, and there was no abstract for the talk: Experimental Studies of Ultracold Few-Fermion Systems in the Dynamics of Ultracold Few-Atom Systems session.

That's certainly unusual. Do you think you could explain why it was so interesting? Sure, let's do that.

Wait, really? You're actually going to blog about real physics? In Q&A format? Yeah, sure. The academic term is over, and the alternative is to read people sniping at each other about politics, which is incredibly depressing. And might lead to writing about politics, which would be worse.

Right, then, few-atom physics. Why is that interesting? Aren't people usually more fired-up about many-body physics? Exactly why I was puzzled by the session title. And since the other three talks all appeared to be theory-heavy, even without an abstract, I thought this was my best bet for finding out. And I'm glad I went, because it was about three really cool papers worth of stuff from the Ultra-Cold Gases group of Selim Jochim at Heidelberg. Jochim was listed as the speaker, but I half remember it being somebody else-- I didn't quite catch the introduction. I'll talk about two of the three papers worth of stuff.

Why not all three? Because the third doesn't appear to have been published yet. The other two are on their Publications page; the final journal articles are linked below in the ResearchBlogging code, but I'll work from the arxiv versions ofDeterministic Preparation of a Tunable Few-Fermion System and Fermionization of two distinguishable fermions, because they're free and I can borrow figures from them.

Fermionization of fermions? Are they in the Department of Redundancy Department? It sounds odd, I'll grant, but actually makes sense. First, though, we need to talk about the preparation of the system.

OK, what are they preparing, and how? Well, like the title says, they're creating systems involving only a few fermions-- they can dial in between 1 and 10 with 90-ish percent fidelity. They start with an ultra-cold gas of lithium-6, which has an odd overall number of protons, neutrons, and electrons and thus behaves like a composite fermion, load them into a very tight laser trap, and then dump most of the atoms away, leaving only a small number of them behind. The basic scheme is shown in the "featured image" at the top of this post-- RSS readers have to click through. They load a bunch of atoms into the laser trap, represented schematically as a sort of "well" in the pictures at the top of the figure, with the energy of an atom increasing as it moves out from the center. Then they lower one side of the trap by applying a magnetic field, and atoms with higher energies leak out. They set the energy level of the "leak" by the applied field, and after they turn it off, they have a deep trap containing a set number of atoms whose energies are below a certain level.

But, wait, why does this give them a set number of atoms? Shouldn't they just get a random assortment of whatever atoms happened to have low energies? Ah, but these are fermions, so they know exactly how many atoms there are in the trap: two per energy level.

Ummm... Maybe you could remind me what a fermion is, again? Oh, sorry. A fermion is a particle that has intrinsic "spin" angular momentum of one-half a fundamental unit, like an electron. These have some unusual properties that SteelyKid once helped me explain, which lead to the famous Pauli Exclusion Principle: no two identical fermions can occupy the same energy state.

The lithium atoms in the trap are fermions, and thus subject to the Pauli principle. In the trap, then, the atoms "fill up" the available energy states-- there are only certain specific energies allowed in the trap, because of quantum physics-- and when they let the higher-energy ones leak away, they know exactly how many they have left over.

OK, but those cartoons clearly show two atoms in each state, a red one and a blue one. Good catch. They have two atoms per state because the Pauli principle forbids identical fermions from occupying the same state. If you put them in two different internal states (represented by the red and blue circles), though, they become "distinguishable" (there's a small subtlety to this that justifies scare quotes, but isn't important for the experiment), and you can have one of each energy state. This becomes important later, so keep that in mind.

I'll try to remember it. So, they set the energy level they want to let escape, and then they know they have two atoms per state below that point? Right. And since their atoms are extremely cold and their trap is extremely tight, they can choose the "leak" point to keep anywhere from one to five energy states, or one to ten atoms, total. They measure this by the amount of light the atoms scatter, which gives them the mean atom number in the figure at the top.

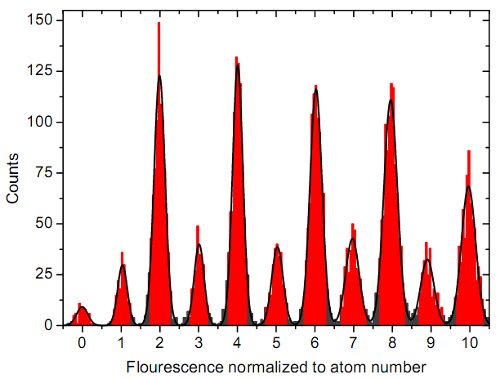
That looks kind of continuous, dude. Yeah, it's not the greatest figure. If you really want to believe in their ability to pick a set number of atoms, the figure you want is this one from the "Supplementary Information" section:

Figure S1 from the arxiv version of the preparation paper discussed in the text.

This is a histogram, showing the number of times in their experiment that they got an amount of flourescence corresponding to a particular number of atoms. The horizontal scale is set after the fact, once they've identified the mapping from light intensity (a continuous variable, binned for convenience) to atom number, and you can clearly see eleven distinct peaks, corresponding to atom numbers from zero to ten.

Why are the even-numbered peaks so much bigger? Oh, wait, it's the Pauli thingy, right? Exactly. They start out with two atoms per state, and the only way to get an odd number of atoms is to set the leak level to a point just barely above the highest state they want to keep, and have one of the two atoms in that state leak out anyway. It's much easier for them to dump atoms two at a time, keeping an even number behind.

Okay, so they can pick between one and ten atoms to keep. Why is this interesting? Well, for one thing, it's just cool to have that level of control. More than that, though, it lets you look at a weird regime of few-body physics. If you have only one atom, that problem is easy to solve, and if you have an effectively infinite number of atoms, there are powerful statistical techniques that can be brought in to get relatively easy answers to anything you'd like to calculate. More than one but less than an infinite number turns out to be really hard, though-- two is mostly doable, three is extremely difficult, four is all but impossible, etc.

Since these guys can dial up a small number of atoms very cleanly, though, they can experimentally investigate this regime, and provide clear results to check theories. Or just motivate people to do theory for this sort of situation in the first place.

Yeah? Give me an example. Well, that's the second paper.

The redundant fermionization thing? Yep, and before I explain that, let me just point out that "Redundant Fermions" would be a great name for a band.

Duly noted. Get on with it. Right, so there's one additional knob they have to turn on this system, which is the strength of the interaction between the atoms. When they have two distinguishable fermions sitting in the same energy level, they're effectively right on top of each other, colliding at high rates. Those collisions change the energy of the state in a way that depends on the details of the collision process. The full physics is very complicated, but what you need to know for these purposes is that applying a magnetic field can change the nature of those interactions in a way that allows them to dial in effectively anything they want. They can make the two atoms occupying a single site behave like they're weakly attracted to each other, or like they repel each other fairly strongly, and anything in between.

That interaction, in turn, determines the exact energy of the two-atom state, and is kind of tricky to calculate. Being able to measure it in a controlled way is a great tool for looking at these systems.

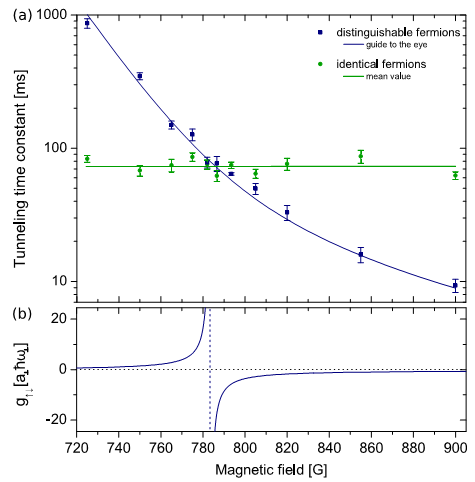
And what do they see? This:

Figure 4 from the arxiv version of the fermionization paper discussed in the text.

This graph shows the "tunneling rate," which is a measure of how quickly the atoms "leak out" of the lowest energy state in the trap, as a function of the magnetic field. The magnetic field, remember, controls the interactions, which determine the energy of the state, which in turn controls the rate at which the atoms tunnel out. The vertical scale is logarithmic, so the blue points, representing the situation where they only have two atoms in the lowest state of the trap, span a factor of 100 in tunnelin rate.

Okay, that's a wide range of control. What are the green points, that don't do anything? The green points are a system that also contains just two atoms, but in different energy states of the trap. The way they do this is by keeping four atoms initially, so each energy state has two atoms in different internal states. Then they selectively throw away atoms in one of the two internal states, leaving only two identical atoms in the trap.

Since these are fermions, and have the same internal state, they can't both sit in the same level of the trap, so one must have a higher energy than the other. They also aren't affected by the magnetic field as strongly-- the interaction strength that changes with the magnetic field is the interaction between two atoms in different internal states. The interaction between identical atoms is only weakly affected, and thus doesn't shift the tunneling rate by any significant amount over the same range of field.

So, how does this represent fermionizaton of fermions? Well, the key feature there is that these two graphs cross each other. So, there's a particualr interaction strength (set by the magnetic field) at which the two "distinguishable" atoms in the same energy state have the exact same tunneling rate as two identical fermions forced to occupy different energy states due to the Pauli exclusion principle. For that value, then, they've "fermionized" the particles that ought to be distinguishable, and thus exempt from Pauli exclusion.

That's kind of cheesey, dude. Yeah, well, it's not my term. And anyway, the mere fact that they're able to play around with the interactions and the fundamental character of these states is pretty awesome, whatever you call it.

Yeah, that is highly neat. So, would you care to close this out with a teaser for this third, unpublished paper whose existence you hypothesize based on the talk? Sure. The speaker also presented some data that aren't in any of these papers, showing the effect of changing interaction strength for systems with different numbers of atoms, from 2 to 10. Again, this is the really complicated range-- you can get an exact solution for one atom really easily, and two with a bit of work, and if you have enough atoms to be effectively infinite, you can use statistical mechanics to get an answer with relative ease.

The system they have lets them look at the experimental value for a bunch of different cases; the two-atom cases fits theory very nicely, but does not match the infinite-number solution. Somewhere between two and infinity, though, the real system of a finite number of atoms has to start looking a lot like the ideal system of an infinite number, and they can investigate where that happens.

Which is...? The subject of their next paper, presumably. I hate to give it away, though...

If I promise to do another Q&A about this stuff when it comes out, can you tell us the number? Four. Four-ish, anyway. But we'll have to wait for the next paper to see exactly.

I look forward to it. Thanks for the explanation-- that was pretty cool. Hey, thanks for giving me something to think about besides depressing politics.

Zürn, G., Serwane, F., Lompe, T., Wenz, A., Ries, M., Bohn, J., & Jochim, S. (2012). Fermionization of Two Distinguishable Fermions Physical Review Letters, 108 (7) DOI: 10.1103/PhysRevLett.108.075303

Serwane, F., Zurn, G., Lompe, T., Ottenstein, T., Wenz, A., & Jochim, S. (2011). Deterministic Preparation of a Tunable Few-Fermion System Science, 332 (6027), 336-338 DOI: 10.1126/science.1201351