"The chess-board is the world, the pieces are the phenomena of the universe, the rules of the game are what we call the laws of Nature. The player on the other side is hidden from us." -T. H. Huxley
There's an amazing interactive application on the Scale of the Universe that was just pointed out to me (thanks, Brian L.), and I had to share! So go play with it (again, link here), and let's talk about it.
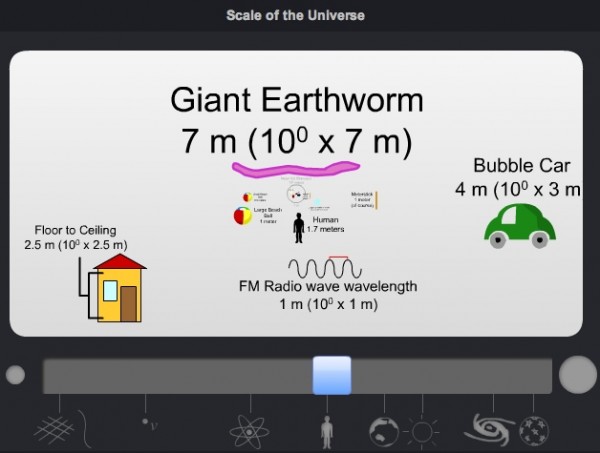
You are here, of course. A human being is somewhere between 1 and 10 meters, to be rough. Being able to zoom from scales as small as the Planck Scale (~10-35 meters) all the way up to the size of the observable Universe (1027 meters) is kind of mind boggling, so let's put it into some perspective for you. With pictures, of course.

So here's a human, and a (perhaps more typical) example of a giant earthworm. These are scales we're comfortable with -- around a meter or so -- and we consider something quite small if it's maybe a few centimeters (or inches), and something quite large if it's maybe 30 to 100 meters (or yards) big.
But we don't have time to step up or down by just one or two factors of ten, or we'll be here all day. Let's go all the way up by around a factor of a million in length, from a human to an entire planet!
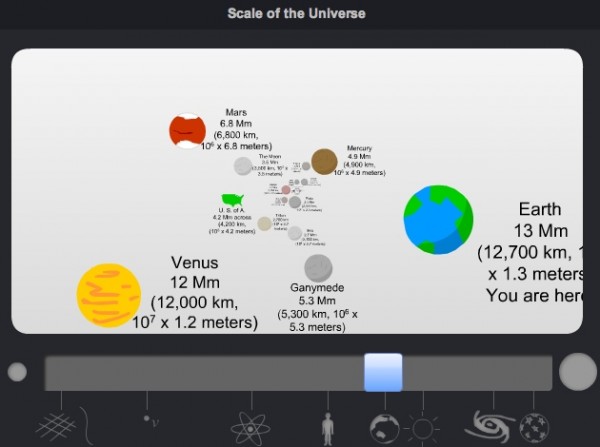
The continental United States, the Moon, the Earth, Mars, and Venus, to name a few, are all about a factor of a million larger in length than a human is, with a size (or radius, where appropriate) measured in thousands of kilometers rather than in meters.

Think, for a moment, about how small you are compared to the planet.
Now, that's the rough size of the steps we're going to be taking. So the size of you compared to the Earth is about the same as the Earth compared to...

the largest stars ever discovered! These are stars the size of the entire Solar System (out past Pluto!), a million times the radius of Earth and more than a thousand times as large as the Sun!
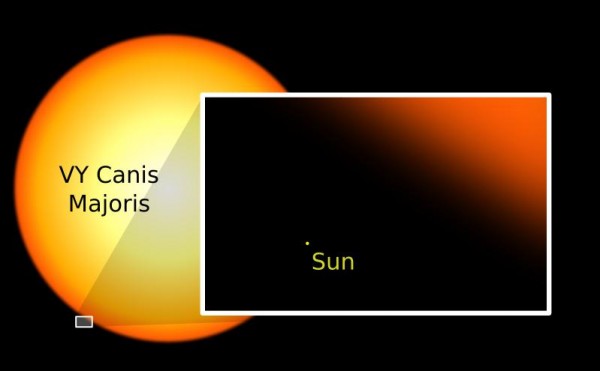
And yet, they're still just one single star. But we can step up by about another factor of a million from these incredible, massive, gigantic Suns. Another factor of a million, larger than these hypergiant stars is...
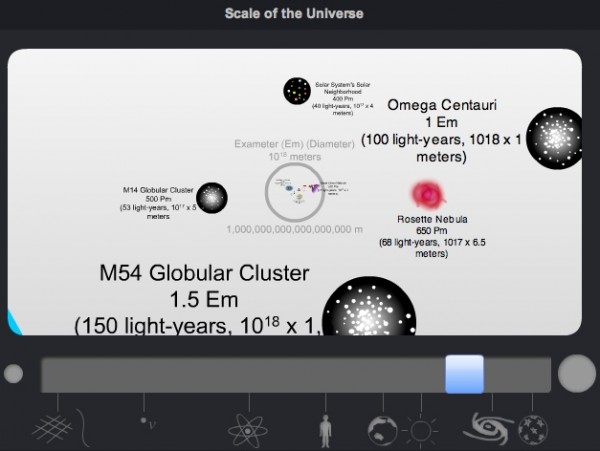
a large globular cluster! These collections of hundreds of thousands to millions of stars span about a hundred light years across! These are the smallest "isolated" objects found in the Universe, and -- like M62 below -- they normally cluster around galaxies.

Remember how large this is! You compared to the Earth is the same size difference as the Earth compared to either the largest star in the Universe or the entire Solar System, is the same difference as that hypergiant star compared to this globular cluster. And to scale up again, this globular cluster -- zooming out by a factor close to a million -- is to...
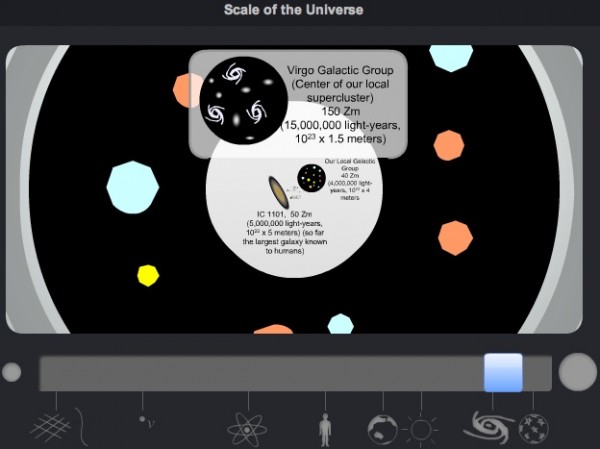
A huge supercluster of galaxies! That's right, bypassing dwarf galaxies, regular galaxies, giant galaxies, the largest galaxy in the Universe, and normal clusters of galaxies, we have gigantic superclusters -- containing tens of thousands of galaxies -- that span tens of millions of light years from end-to-end.

And I'd love to scale up by another factor of a million or so, but I can't. Why not?
Because I run out of Universe.
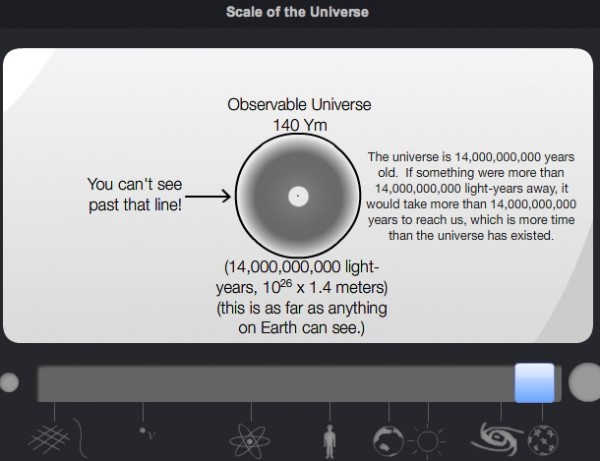
Contrary to what the website tells you, when the observable Universe ends, so does our definitive knowledge. If the laws of physics are, indeed, the same outside of our observable Universe as they are inside, then we can conclude that the "actual" Universe is at least 150 times as large as the observable part, much bigger than that site claims. In fact, if inflation -- as we understand it -- is true, it's quite likely that the Universe is many trillions of times larger than our paltry observable part.
But at the very least, we can place a lower limit on the size of the Universe based on what we see. And, suffice to say, it's huge.
But what, now, if we went the other way? From humans, instead of larger scales, what if we put away our telescope and broke out our microscopes? What would we see?
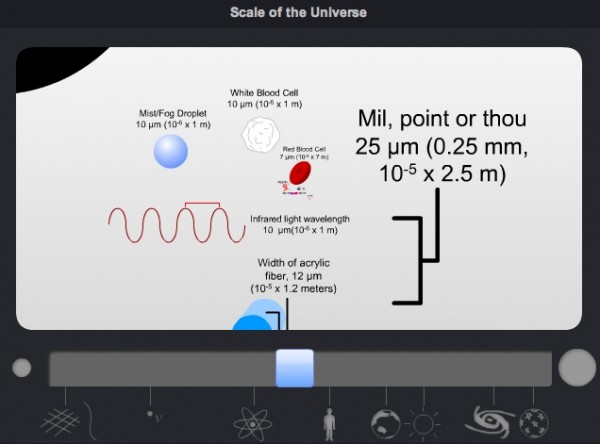
Well, going down to the scale of maybe ten microns, we bypass things like pollen spores, dust mites, and the paramecium, and come all the way down to individual blood cells. Tiny, tiny things. A single blood cell compared to you is slightly larger than you compared to the Earth.
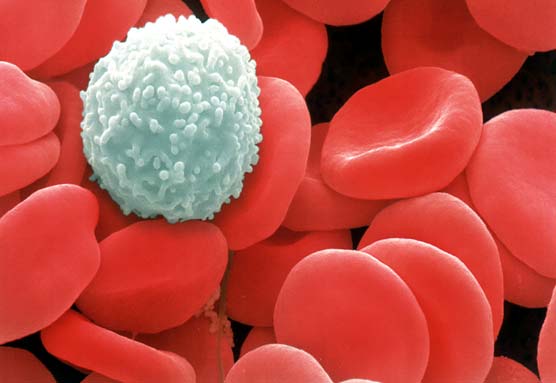
And remember, your lone body contains somewhere around 40 billion blood cells at any given time. And if I went down by another factor of a million from here, I'll pass by everything interesting. All the most primitive cells, the tiniest virus, a single strand of DNA, a single molecule, everything. A blood cell to a human is the same scale as...
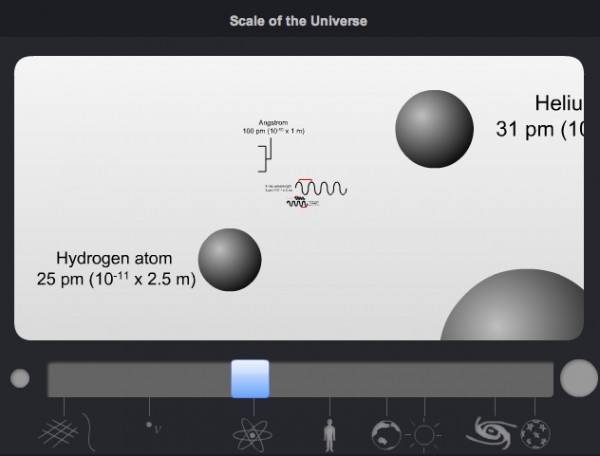
the smallest single atom in the Universe, hydrogen, is to a single cell. Hydrogen, the simplest atom out there, with just one proton and one electron.

And yet, I can go smaller still. Another factor of a million takes me inside the atom's nucleus, inside a single proton, down to the smallest subatomic constituents I know of.
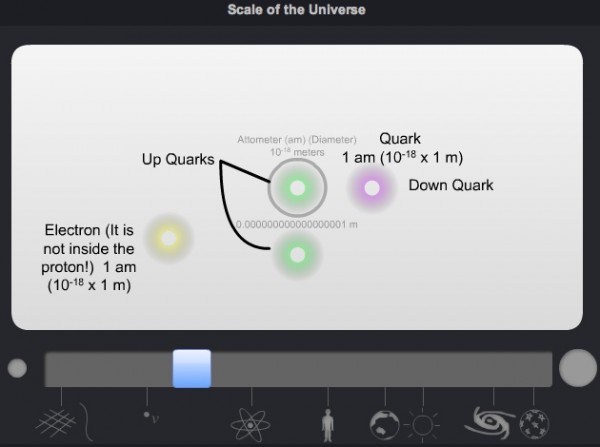
Kind of. These fundamental constituents of matter -- as far as we can tell -- aren't 10-18 meters in size. They're constrained, by our strongest particle accelerators, to be less than 10-18 meters in size!

In other words, all the sizes less than or equal to 10-18 meters are upper limits! While the interactive demonstration will take you smaller and smaller, and will show you (possibly fictional) particles like preons and strings, this brings us to the particle physicist's nightmare. What if all of these subatomic particles: quarks, gluons, electrons, neutrinos, etc., are really, really tiny?
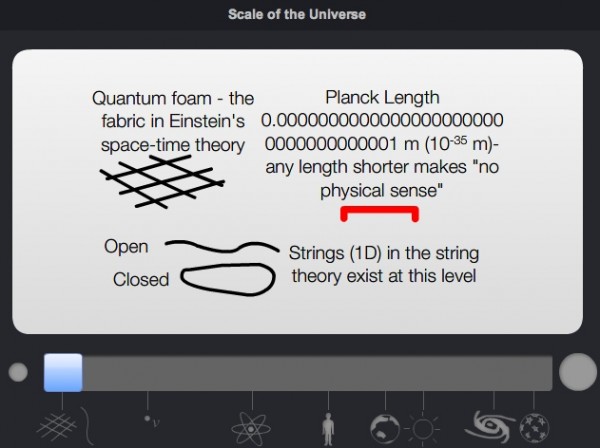
What if they go all the way down to the Planck scale, for example?
It would mean that -- other than the Higgs -- there are no new particles to find by building accelerators. (Not, at least, until we build an accelerator larger than the Solar System.)
And that's the Universe we know, from the largest to the smallest, as we run up against the limits! What lies beyond? Well, like Huxley said, the other side -- at least for the time being -- is hidden from us.
Hope this takes you into a great weekend!

"I was like a boy playing on the sea-shore, and diverting myself now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me." -Isaac Newton
Thanks for the work and care that you seem to have put into this missive. But stop being so special! Use some discipline. There's a small chance you may have something worthwhile to contribute.
Nice picture of a static universe there, Fred!
/Muttley snigger ;-)
I love that website. I love anything that gives me the feeling (however fleeting) that I actually can grasp all these different scales.
However, isn't the 14,000,000,000 LY distance incorrect as the size of the observable Universe?
http://scienceblogs.com/startswithabang/2009/07/the_size_of_the_univers…
Instantly reminded me of "Total Perspective Vortex"
http://en.wikipedia.org/wiki/Total_Perspective_Vortex#Total_Perspective…
I've a question for Ethan or anyone who's familiar with Planck length. I was curious where does it come from and what kind of thing does it capture so I checked the wiki article on it but it made me more confused. For instance, it says,
"The physical significance of the Planck length, if any, is not yet known. Because the Planck length is the only length that can be formed from the constants c, G, and ħ, dimensional analysis suggests that lengths of special significance in quantum gravity are likely to be small multiples of the Planck length."
Is this correct? Where does the Planck length come from? What does it mean that it's the smallest length that makes sense?
c and G are the fundamental constants in General Relativity which describes space-time. ħ is the fundamental constant of quantum mechanics. There's reason to think that a theory of quantum gravity will involve a discretization of space-time, implying a smallest lengthscale. A reasonable estimate for this scale can be made heuristically by putting the three mentioned constants together. But I think it also arises quite naturally in our existing attempts at quantizing gravity.
The really fascinating thing here is that we, human beings, have figured this stuff out.
From the man - earthworm scale, measured and noted millenia ago, to the newest astronomical and subatomic discoveries of the last decades, we have figured this out.
This to me is the most amazing part of the story.
This reminds me of when I was working at a science center in CT in the late 70's, and we got a new film to show the visitors: Powers of Ten. I actually found it on YouTube!
http://www.youtube.com/watch?v=0fKBhvDjuy0
Just to show how knowledge has increased since 1977 when it was made... the big end doesn't get into the large-scale filament structure of the universe, and on the small end, it stops at the proton, and only hints of quarks.
Can Ethan or anyone else clarify for me how one can talk about the specific age of the Universe as a whole without presupposing some sort of an absolute time scale?
Can Ethan or anyone else clarify for me how one can talk about the specific age of the Universe as a whole without presupposing some sort of an absolute time scale?
Just start counting from now as your 0. If you count every year back you get to 14 odd billion years to inflation.
I love this scaly-thingy. I sent the link around to my fellow faculty. It's especially helpful given that none of my (college!) students knew how long a meter is. *sigh*
Still, it's my job to teach them, and this helps. I only have one complaint, though: after all the Planck-length stringy stuff, where are all the turtles?
I suspect Boom is surprised by the idea that everyone in the cosmos can do that, making it look like we've ditched relativity and gone back to having a Newtonian absolute time.
12 WROTE: Just start counting from now as your 0. If you count every year back you get to 14 odd billion years to inflation.
14 WROTE: I suspect Boom is surprised by the idea that everyone in the cosmos can do that, making it look like we've ditched relativity and gone back to having a Newtonian absolute time.
********
You are absolutely right, Phayes. That's precisely what I wanted to have clarified. If the universe is supposed to "look the same" to every observer, then every observer can do this "counting backwards" (as suggested by Brian) to arrive at the same figure for the age of the universe. And that looks like an absolute time scale of sorts.
Now I am sure that I am simply missing some technical aspect of GR which would explain away this appearance of absolute time scale (on which the age of the universe is measured). That's why I thought that Ethan or someone else here would be kind enough to clarify this issue for me.
Yes - it is an absolute time scale of sorts, and the reason for its existence is that the Cosmological Principle (every[i]where[/i] is isotropic) turns out to be such a strong condition that it restricts the possible form(s) of the metric for the whole of spacetime (the cosmos), and its dynamics, to just a few simple ones that have this feature.
@Boom: The time "14 billion years" is the time measured by so-called "co-moving observers". That rather technical looking term simply means that the observers only move along with the expansion of the universe, but have no extra velocity on their own (you probably know the balloon analogy for the expansion for the universe? in that analogy, co-moving observers are the ones which are glued to the surface to the balloon; things which crawls over the surface are not co-moving). All such observers will measure the same time; observers who are not co-moving will measure another time, depending on their velocities.
(technically, you also have to specify that the observers are not in a gravitational well, but we'll leave this out here ;-) ).
@bjoern (17):
Thank you for the clarification, although now I wonder: if the fact that "comoving co-ordinates" assign CONSTANT spatial coordinates to observers to whom the universe looks isotropic, why doesn't this smuggle in some sort of notion of "absolute rest" w.r.t. the universe?
Again, I am not questioning anything about GR or cosmology. It is only my lack of clear grasp on the "meaning" of "cosmological time" that is bothering me.
While we're on the subject of mind-boggling scales with respect to the universe, are there any estimates of just how fast the universe must have been expanding during inflation? If the universe is anywhere from 150x to several million times what we can observe (as Ethan states here), the universe must have been expanding at many powers of the speed of light, correct? I imagine reducing such a figure to a human scale of miles or km per hour would be a pretty tough number to wrap your head aound.
@Boom
Last comment from me: coordinates are *irrelevant*. Furthermore, the concept of â(absolute) restâ simply has no meaning for non-coincidental events in spacetimes. For example: the phrase, ârecession velocityâ - which even pollutes the otherwise excellent well-known cosmology myth debunking paper by Davis and Lineweaver - is utterly meaningless.
@Boom: Well, that depends on what you mean with "absolute rest". ;-) It is true that one can indeed determine one's velocity "with respect to the universe", i. e. with respect to a co-moving observer (simply measure the Doppler shift of the CMBR). But this does in no way contradict Relativity, since Relativity only says that there is no absolute rest frame in the sense that the laws of nature have the same form in all frames. It doesn't say that you must have the same values for all physical quantities in all frames.
@yogi-one: Velocity is change of position or length with time, essentially. So if you want to talk about the expansion velocity of the universe, you first have to specify what length you are talking about. Its radius? Its diameter? Or what? (oh, and you probably meant "at many times the speed of light", not "many powers")
I guess it would be void, just black emptiness.
its hurts my brain when I think of time before the universe. A theory says that we are a giant cosmic bubble which is the universe living in a sea of cosmic bubbles (different universes)
So is beyond the sea of the cosmic bubbles what created the sea of cosmic bubbles?
And was before existence? if thats even possible.
Wow! You don't want to find one of those in the back of your yard.
I've got a question for Ethan or any one who knows the facts or the lack of them about the following: I have been told by a Nuclear Science professor that the further away from us, for example, you look out into space the faster the stars etc are moving away (from us). He says near the limits of the universe stars are traveling near the speed of light. He says if you could travel faster than the speed of light causes would come before effects. He doesn't believe it could happen but then he says out past the "limits" scientists do believe objects are moving away from us faster than the speed of light and therefore we'll never see them. Is this all true? Any comments as well?
i like it
"scientists do believe objects are moving away from us faster than the speed of light and therefore we'll never see them. Is this all true? Any comments as well?"
Read up on the Inflation theory, Mark. It isn't that the objects are travelling faster than light, but that some time in the past the space between objects grew faster than light, leaving the photons stranded "closer" to the object relative to their distance from another obhect and therefore requiring more time to reach the observer than there's been time for the light to travel that distance.
there has to be and end sooner or later right? or maybe the unvierse is like something small in a bigger thing...