"Mortal as I am, I know that I am born for a day. But when I follow at my pleasure the serried multitude of the stars in their circular course, my feet no longer touch the Earth." -Ptolemy
When you look up at the stars in the night sky, perhaps the most striking thing that they do is rotate about either the North or South Pole, depending on which hemisphere you live in.

But what do you get if you look up at the same time each evening, night after night?

Well, unlike the planets Mars (in red) and Uranus (faint, to the upper right of Mars), the stars stay in the same exact spot from night to night. Yes, they're moving, but they move far too slowly for how far away they are to detect their motion.
So how would you determine how far away a star is? Well, if your name was Nicolaus Copernicus, you'd look up at the positions of the stars at one night, and you'd look up six months later, and see if any of the stars have moved.
Why would you do that? Play along with me for a moment. Close your left eye, and hold your right arm out straight, with your thumb pointing up. Pay close attention to where your thumb appears to be relative to everything around you.

Got it? Good. Now, leaving your thumb in the same exact spot, open your left eye and close your right eye. Notice where your thumb appears to be now.

It appears to move! You can play with this all you like, but you'll not only notice your thumb always moves when you switch eyes, it appears to move by a fixed number of degrees dependent on two things only: how far away your thumb is from your eyes and how far apart your eyes are! In astronomy, we call this parallax.
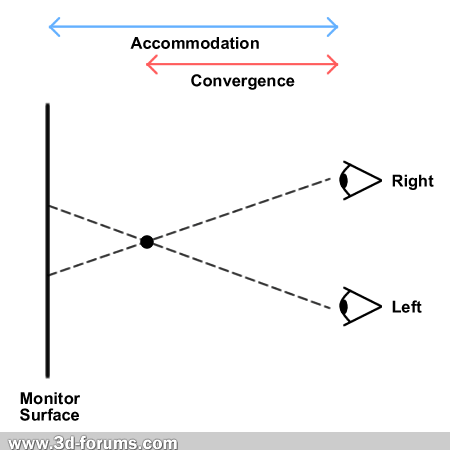
Back to the stars now. When you make an observation of the stars, your eyes are way too close together to see any sort of "apparent shift" of a star. In fact, the diameter of the Earth is far too small! But Copernicus, realizing that the Earth goes around the Sun, would have seen his position shift, over the course of six months, by about 300 million kilometers! So, he reasoned, he should be able to see the closest stars in a different apparent position, like so:
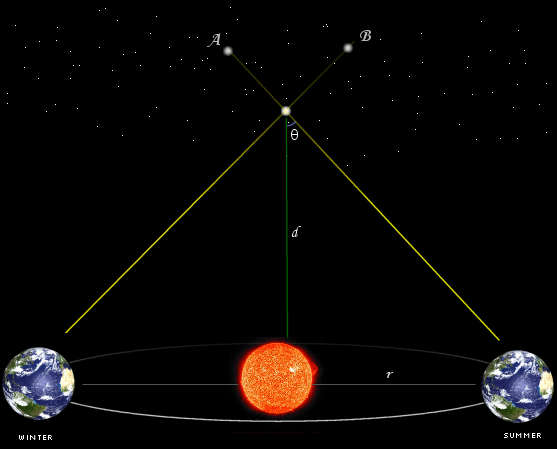
Of course, Copernicus didn't see anything because the telescope hadn't been invented yet! The first astronomical parallax wasn't discovered until 1838, and that was by Friedrich Bessel.
![bessel[1]](/files/startswithabang/files/2010/05/bessel1-600x507.jpg)
(And yes, for those of you who are wondering, it's the same guy who did Bessel Functions.)
Once you can measure the parallax of stars, the one with the largest parallax will be the closest one to you. (And if you want the answer, it's Proxima Centauri, at 4.2 light-years distance.)
But what if you lived before 1838? What if you still wanted to know the distance to the stars; would you have any recourse?

Not until the mid-1600s did someone -- Christiaan Huygens -- make some great progress on that front. Huygens was already famous for inventing the pendulum clock and discovering Saturn's rings and its great Moon, Titan. But the stars were another story. Huygens' big idea was that the stars in the sky were identical to our Sun, but much farther away.

Since he knew how bright the Sun was and how far away it was, he reasoned that if he chose the brightest star in the sky and was able to figure out its brightness relative to the Sun's, he could figure out its distance!
So he found the brightest star in the sky, Sirius, and studied it.

The next day, he went and took a large brass plate and drilled holes of different sizes in it. He held the disc up at arms length, covering the Sun entirely. Well, except for the holes he drilled in it! And so he studied the tiny bit of Sun poking through the holes, looking at progressively smaller and smaller holes until he found one that matched Sirius.

At least, that was the plan. It didn't work, though. No matter how small he made the holes, the tiny bit of Sun that shone through was always significantly brighter than Sirius! So what did he do? He went out and got a bunch of opaque glass beads, reducing the amount of light that came through even further.
And it wasn't until he reduced the amount of light coming from the Sun by a factor of about 800 million that he was satisfied. This meant that -- roughly -- this star was 28,000 times farther away than the Sun was from Earth!

If you work this out in modern units, his estimate comes out to about 0.4 light years. But if you head on over to wikipedia, it'll tell you (correctly) that Sirius is 8.7 light years away. But it will also tell you that Sirius, intrinsically, is 25 times more luminous than the Sun is!
In other words, if you know something about how intrinsically bright a star is, you can figure out how distant it is without a telescope, and just by creatively destroying one of your dishes!

How was Huygens able to judge the brightness of the sun against the brightness of Sirius when he could only even see one or the other? How could he get an objective measure of brightness at all?
He had a photographic memory. [rimshot]
I'll be here all week, folks. Be sure to tip your server!
There is a way to measure distances using the brightness:
m - M = 5log dpc - 5
Solving for d, gives:
dpc = 10(m - M + 5)/5. The distance, dpc, is given in parsecs. Then the distance in lightyears, is given by
dly = 3.26/dpc
How far away is the parallax useful and how do you account for the motion of the sun relative to the other stars?
@4: The distance at which you can measure parallax depends on the angular resolution of your telescope. The parsec, mentioned in comment #3, is the distance at which the parallax due to Earth's orbital motion is one second of arc. The parallax you will measure for a given object is inversely proportional to its distance. As for relative motion of stars: We can take the Sun to be at the origin of an inertial reference frame, and it is possible with several years of observations to detect the transverse (relative to the separation vector) motion of nearby objects (motion along the line of sight, which is measured by a different technique, does not come into play in this discussion). The "proper motion" of a star will add up over the years, whereas the motion due to parallax is a back-and-forth motion.
Flavin: He was working entirely from memory, yes.
From wikipedia:
"He was also the first to measure the parallax of Vega, although Friedrich Bessel had been the first to measure the parallax of a star (61 Cygni)."
Isn't Vega a star? If so, then Struve would be the first one who calculated the distance of a star using parallax method...
No, no, no, Karl. The Vega was a car introduced by chevrolet in 1971; not a star.
I don't know why I couldn't resist that. Sorry.
I don't understand how Huygens could gauge the relative brightness of Sirius to the sun when he can't see them side-by-side. (As Flavin points out in #1.) Did he have a photometric mind or was it a very lucky guess? Did he do it by diminishing the light of Sirius until he could no longer see it then put himself in a dark box and do the same for his disc with holes and the sun? I'm awful at gauging the relative brightness of objects and I'm easily fooled by gradients.
Now Newton made a reflecting telescope and in his era there were moderately large refractors - so did people repeat Copernicus' experiment but it took much longer for someone to actually look at the right star and record a difference?
@Feedayeen #4: Thanks to folks like Michelson, measurement of parallax was very useful because the parallax could be used to measure the apparent width of the closer stars. The fundamental limiting factor is how far apart you can place your two effective apertures. On earth this horrible thing called an atmosphere places some practical limitations on what can be accomplished, but the Keck Observatory has the most awesome visible/IR interferometer on the planet. There was a proposal for a space-based very long baseline interferometer but I think that's died out for the moment; there were just way too many challenges to overcome (including the requisite funding). As people make gradual progress with various technologies perhaps one day a stellar interferometer would be put into space - but it would have to be able to provide research data which interferometers such as the Keck cannot provide, and by that I mean data which will help answer questions and not just data for its own sake.
It's also worth pointing out that from the classic Greek era to Ptolemy's time (he was of Alexandria, somewhat later) the geometrical simplicity of a heliocentric system relative to the geocentricism was understood but rejected...not because of resistance to the idea of an Earth in motion (though that was a stumbling block), but mostly due to the observed lack of parallax of the stars. This implied a distance to the stars to be far, far, far beyond anything conceivable at the time and was just too insane to accept. And, really, most people today ostensibly accept astronomical scales but, in fact, have no intuitive grasp of the vast distances involved.
There is a couple of different levels of sophistication of the popular conception of geocentricism. The least sophisticated view is that the ancients were just ignorant and thought the Earth was flat, that it didn't move, and that it must necessarily be, as a matter of ideology, the center of the universe. The first was certainly not true (people in many cultures throughout history have understood the world is a sphere; it's frankly obvious); the second people did believe, but not as a matter of necessity; and the third people also believed, but were prepared (in some places and times) to consider the alternative.
The more sophisticated, and actually less accurate and fair, criticism of geocentricism is that the astronomy and geometry was stupid and overly contrived. However, Ptolemaic astronomy remained more predicatively accurate for many years after the development of heliocentricism because it was a very highly tweaked observationally-based model. As for being stupid and contrived, well, in my opinion the ridicule heaped upon epicycles is unwarranted and it's really the "equant" (a point about which the constant rate of angular motion was centered, but not the path) where Ptolemaic astronomy gets a little unwieldy and arbitrary. Epicycles themselves are reasonable. And, in any case, it was an accurate model that fit what was known and thought to be acceptable about reality at the time. Eventually, the notion of a much larger cosmos and an Earth in motion became more "thinkable" and that allowed the simpler math of heliocentricism to be ascendant. It was a while, as Ethan explains, before observations either validated or made heliocentricism necessary.
If you study outdated and disproved scientific theories in their proper historical context, they almost never seem as wrongheaded as they do from our contemporary point-of-view. And there are, no doubt, some widely accepted contemporary natural "truths" about which our descendants will shake their heads and wonder at our cluelessness.