How lucky would Kepler have to be to see us?

Posted by Ethan on June 18, 2010
(12)
More »

“No pessimist ever discovered the secret of the stars, or sailed to an uncharted land, or opened a new doorway for the human spirit.” -Helen Keller

If you’ve been paying attention, you heard that the Kepler mission, earlier this week, announced the discovery of 706 candidate planets orbiting stars in its field of view.

And while most of the planets it found were Neptune-sized or smaller, they were still mostly gas giants, and still mostly closer than Mercury to their parent stars. Kepler’s looking at 100,000 stars, and while finding 706 planets is certainly not bad for just over a month’s work, there’s a big question to be asked.

Where are the planetary systems like ours?

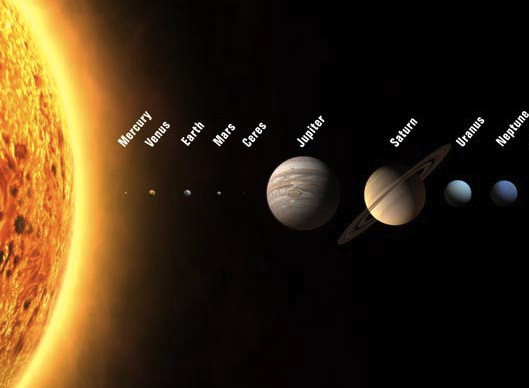
To answer that, I’ll run through a little hypothetical analysis with you. What if one of the stars Kepler was looking at was just like ours? What if an identical copy our Solar System was sitting out there, 10 parsecs (or so) away, and Kepler had the good fortune to be looking at it? What are the chances we would find something interesting?

Would it even be lined up correctly? If the planets are misaligned with respect to us (like Saturn’s rings sometimes are with respect to Cassini),

they’ll never block any of the Sun’s light! Unless the planet sometimes sweeps directly in front of the star, blocking the light during a transit,

we’ve got no chance of seeing anything. Well, how accurate would this alignment need to be to see the different planets? And what are the chances of that happening, considering that orientations of solar systems appear to be completely random?

Let’s investigate, for each planet, how good the alignment would have to be for Kepler to see something:

Planet Degree Range (out of 180) % chance of good alignment
Mercury 1.37 degrees 0.76% chance
Venus 0.738 degrees 0.41% chance
Earth 0.533 degrees 0.30% chance
Mars 0.320 degrees 0.18% chance
Jupiter 0.101 degrees 0.056% chance
Saturn 0.0556 degrees 0.031% chance
Uranus 0.0277 degrees 0.015% chance
Neptune 0.0177 degrees 0.0098% chance

 

Take a look at what that means. To get an alignment fortuitous enough to see even Earth, we’ve only got a 1 in 200 shot. Want to grab Neptune? Forget about it; you’re down to a 1 in 10,000 shot! In other words, when you hear that Kepler “only” found 706 planets orbiting 100,000 stars, keep in mind that it can’t see most of them because they’re not “edge-on” (lower right) to our line-of-sight!

But there’s even more to the story. Even if we were lined up perfectly, we might not have seen something yet. Remember, Kepler has to observe for long enough to observe the planet both begin and end the transit — and for confirmation, repeat itself — before we have a good planetary candidate.

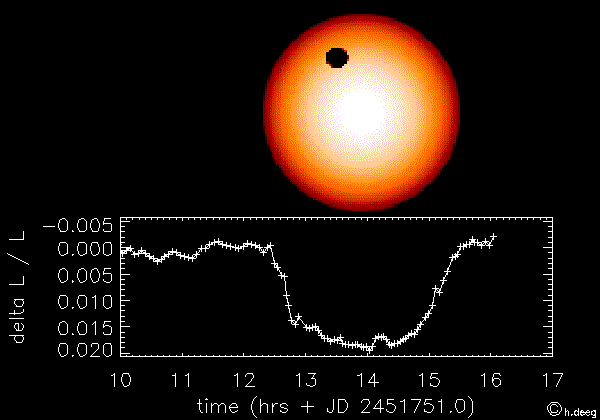
Assuming we did have a good alignment, how long would it take each planet to transit the Sun? And how long does the planet take to make an entire orbit? And what’s the percent chance that Kepler would have seen it yet, after 33.5 days?

Planet Transit time Orbit time % chance after 33.5 days
Mercury 8.07 hours 88 days 38.1% chance
Venus 11.0 hours 225 days 14.9% chance
Earth 13.0 hours 365 days 9.17% chance
Mars 16.1 hours 687 days 4.88% chance
Jupiter 29.6 hours 4332 days 0.773% chance
Saturn 39.9 hours 10759 days 0.311% chance
Uranus 56.7 hours 30799 days 0.109% chance
Neptune 71.2 hours 60190 days 0.056% chance

 

Keep this stuff in mind when you see results from Kepler. We’re not very likely to see planets that are any significant distance away from their star unless we wait for many, many years. And mind you, that’s only if the alignment is very good, which — for nearly all planets — it isn’t likely to be!

What does this mean, overall? That if every one of the 100,000 stars Kepler is looking at had a solar system just like ours, then by this point, we would have expected Kepler to have found 391 planets. Their actual findings so far? 706 planetary candidates. I’m just saying here, we’ve got every reason in the world to be optimistic! We’ll know more when they release more data in February of 2011!

(12)
More »

Comments

  1. #1 Scott
    June 19, 2010

    What does this mean, overall? That if every one of the 100,000 stars Kepler is looking at had a solar system just like ours, then by this point, we would have expected Kepler to have found 391 planets. Their actual findings so far? 706 planetary candidates.

    o_O So means that we can revise our estimate for planets in the universe to a metric fuckton?

  2. #2 Torbjörn Larsson, OM
    June 19, 2010

    Right. Now if I understand the problem correctly from the above, I should be able to deconvolute the sampling distribution from the raw data and see how planets likely distribute over orbital radius. IIRC the Kepler paper didn’t do that, so there is no handle on how many Earth analogs we expect now, or in the Kepler field of view. Presumably these numbers aren’t frighteningly close to zero. [goes away mumbling]

    @ Scott:

    I believe you mean measure, as a metric is a distance function with properties like the triangle inequality.

    Though if this embarrassing richness of planets stand up everywhere, number of planets will _behave_ as a metric if you look at sum of planets within a distance from us (say).

  3. #3 NewEnglandBob
    June 19, 2010

    Thanks Ethan, and thanks to others who responded to my questions on the previous post.

  4. #4 andy
    June 19, 2010

    I disagree with your estimates for transit probability, your values are too low.

    You can’t just divide the allowed misalignment range by 180 degrees as you appear to have done here, you should be working in terms of surface area on a sphere. Take the z-axis of the sphere as pointing towards/away from Earth, and the normal vector of the orbit corresponding to a point on that sphere. Then transits occur when the normal vector is close to the sphere’s equator, and most of the surface area of the sphere is near the equator rather than the poles.

    So for example for the Earth to transit, the orbit vector must fall into a range of 0.533 degrees of latitude centred on the equator. This corresponds to 0.46% of the sphere’s surface area (which means the transit probability is 0.46%, rather than the 0.30% you have given).

  5. #5 dave w.
    June 19, 2010

    This is the best explanation of have seen about the ease (or difficulty) of planet spotting. Thanks Ethan, you make us non-scientists feel real smart!!!

  6. #6 Jon
    June 19, 2010

    Thanks for another great post. Just trying to get my bearings in the Cygnus/Kepler Field of View photo: Compared to Orion’s belt, how large does Cygnus appear in the night sky? Or, how many degrees of arc is Kepler looking at?

  7. #7 DataJack
    June 19, 2010

    Thanks, Ethan, I have always wondered about that. It’s great that there are probably many more planets then we originally thought. Also, it is sad that we will not know about them for a long time, if at all.

    My opinion is that almost all stars have lots of planets. So this increase the Drake Equation findings from 10 advanced civilizations in our Galaxy now to 20! Hrmph – I think there are millions. But I think they will all stay forever isolated from one another, because FTL is impossible, and interstellar travel is impractical to an extreme.

  8. #8 George Anderson
    June 19, 2010

    This is a great explanation of why we’re not finding anything smaller then gas giants so far. Sounds like the chances of finding a solar system just like hours have worse odds then the weekly lotto.

  9. #9 Brent
    June 19, 2010

    This isn’t really changing how many planets we think there are… what we’re seeing here is that there are a lot of solar systems with planets that are easier to spot than our own. Which isn’t really a surprise, because we’ve been finding solar systems like that for years without Kepler, and had already figured that they weren’t particularly rare.

    What we have here is really a tortoise and hare thing… right now, Kepler is going to be spotting all of Hot Jupiters it can because they’re they’re so close to their star they’re racing around it like rabbits giving plenty of opportunities to see and confirm them… so they’re going to show up significantly in the numbers right now. But as time goes by, the new solar systems it finds are going to be increasingly more like ours (because it will have already seen all the Hot Jupiters well before then)… where the gas giants are far enough out that their orbital periods are measured in decades.

  10. #10 rob
    June 21, 2010

    since Kepler has found almost double the number of planets expected, that must mean the each star has *2* solar systems!

    (it seems strange, i know, but 5 out of 4 astrologers i polled agree)

  11. #11 daedalus2u
    June 22, 2010

    The probability estimates are wrong for another reason, the distribution of orbital planes of stars in Earth’s near vicinity are not isotropic and random. Any planetary system would be derived from the same gas cloud that the star formed from, and would co-rotate with it. I presume that many stars in Earth’s vicinity also rotate in approximately the same direction.

    The distribution of stars is not isotropic either.

  12. #12 cay
    June 26, 2010

    A 6-8 Mega terrestrial planet has been discovered by Kepler (I saw the light curve data from a student of mine at Harvard!)