"...it is reasonable to hope that in the not too distant future we shall be competent to understand so simple a thing as a star." -Arthur Eddington, 1926
(For Mike H., who wanted to know.)
The Sun -- like nearly all stars -- burns bright through its nuclear reactions, sending light, heat and energy out into the Universe over a timespan of billions of years.
But it didn't need to be that way. With the mass of about 300,000 Earths, nearly all of it in the form of hydrogen fuel, you can just as easily imagine a huge nuclear explosion on the scale of an entire star, burning all of the Sun's fuel up in a tiny fraction of the time.

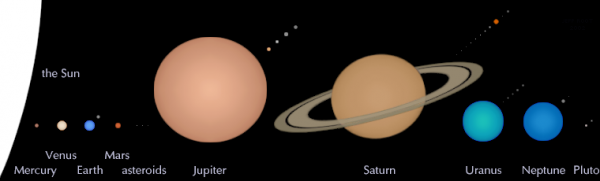
Let's take a look inside, and find out why the Sun takes billions of years to burn its fuel up. And let's start by comparing the Sun with the rest of our neighbors: the planets in our Solar System.
When you take a look at the inner planets, it's no surprise that Mercury, the smallest planet, is also the least massive. Mars is next, followed by Venus and Earth, which are close in both mass and size. And this makes a whole lot of sense: you pile more and more atoms on top of one another, and where you've got more atoms, you get a larger and more massive object in the end. But at the heavy end, there's a bit of a surprise.
Saturn -- the second largest planet in our Solar System -- is nearly the same size as Jupiter, with a diameter about 85% as large as its Jovian superior. But in terms of mass? Saturn has only one-third the mass of Jupiter! To understand what's going on, we've got to go down to the atomic level.
There's not some atomic catastrophe at play here, where Jupiter is made out of gold or some other incredibly dense element. Instead, Jupiter and Saturn are made out of nearly identical stuff, but Jupiter really has about three times as much of it as Saturn does.
The big difference is that Jupiter has so much mass that the atoms themselves start to compress one another at the center, packing them tighter and tighter together as more mass accumulates.
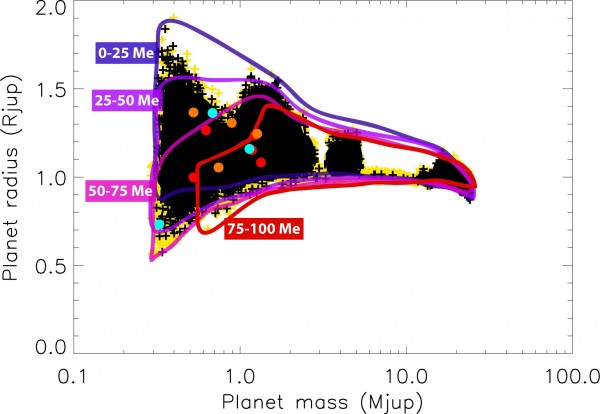
This has gotten really fascinating as we've discovered planets outside the Solar System, because as planets get much more massive than Jupiter, they start to get even smaller in size.
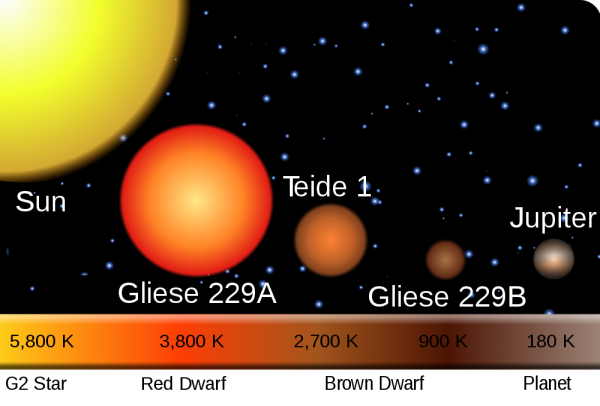
As you make your object more and more massive, it continues to shrink and shrink. By time your planet is about 13 times 70 times (thanks, Ned Wright) as massive as Jupiter -- or about 8% as massive as the Sun -- the hydrogen atoms at the core are so dense and under so much pressure that they can actually begin fusing together into heavier elements!
And when that happens, your "too-big-to-be-a-planet" mass expands. When you were just a planet, gravity pulls inwards on all of your atoms, attempting to collapse them down to as small a space as possible, but the atoms themselves can resist it. But once you achieve too great a density at too high a pressure, and fusion starts, you begin turning mass into energy. And what does this energy -- in the form of radiation -- do?
It pushes outwards. Rather than atoms holding up a star against gravity, it's now the radiation from the nuclear fusion you began. A low-mass star like a Red Dwarf is many times larger than Jupiter, while a star as massive as the Sun is significantly larger still.
And for our Sun, the energies we're talking about are huge! Every single second, the Sun fuses six hundred million tonnes of hydrogen into helium! And while that gives us a huge amount of energy, remember that the Sun itself is also huge.
Those six hundred million tonnes of hydrogen that get fused every second happen in the Sun's core: the innermost 20% of the Sun (by radius). But remember that the Sun is 700,000 km in radius; you could line up more than 100 Earths across its diameter! If you break it down by volume, you find that the Sun produces "only" about 300 Watts per cubic meter, or the amount of body heat generated by two adult male humans.

(So yes, a crowd of humans the size of the Sun's core could produce just as much heat as the Sun, in theory. That is, as long as you can keep them alive.)
This is probably very different than your conventional view of fusion, which likely takes a small "mass" like this...
...and turns it into a huge, many-mile-wide explosion, like this.
Paradoxically, then, the lower your star is in terms of mass, the dimmer it is, the cooler and redder it is, and the longer-lived it is, too!

A G-type star like our Sun may live from 10-15 billion years, while a low-mass, dim red dwarf star (an M-star) may live anywhere from hundreds of billions to many trillions of years, far longer than the age of the Universe!
But on the other side, as you get more and more massive, your fusion-burning core gets progressively larger and larger. The largest, bluest O-stars weigh in at more than 100 times the mass of our Sun, and burn through their entire complement of hydrogen fuel in less than one million years!
Amazingly, for all hydrogen-burning stars like our Sun, the only major determinant for the star's lifetime is its mass.
So even though it might not look it, the reason the Sun burns its fuel at the rate it does is because this is the right rate for its mass. Given that nuclear fusion produces the radiation necessary to cancel out the Sun's gravitational force throughout its interior, it's this nuclear burning that keeps the Sun from either expanding or contracting. (Variable stars have missed this equilibrium mark, and expand due to too much radiation, then don't produce enough radiation and contract, and then fuse more atoms together and expand again. Or maybe not.) The larger your star is, the more radiation is pushing out and the faster you're burning through your fuel.
And that's how the Sun works, from the inside out!






Thanks, Ethan. I had suspect that larger stars would be shorter lived, but am completely surprised that dwarf stars would last so incredibly long.
Mike,
The mathematical relationship is that the lifetime of a star is inversely proportional to the mass of the star cubed. (Some people make the exponent 2.5, some people make the exponent 4, but it's somewhere in that neighborhood.) So a star one-tenth as massive as our Sun will live 1,000 times longer, and a star 100 times as massive lives only 0.0001% as long.
Dude, you didn't even mention the importance of Heisenberg! That was what knocked me on my ass when I learned it, which was not until an intro astronomy course in college. The professor (this is David Helfand, if you're familiar, who's still head of the astronomy department) worked out for us, based on the electrostatic repulsion between two protons and the distance at which the strong force overpowers it, how fast they'd have to be moving towards each other to get that close. (I forget the value, I think it was around 0.1c or so.) He then said, "There are about 10^57 protons in the sun, and exactly ZERO," and draws a huge goose egg on the board, "of them are going that fast." And proceeded to explain how it's only due to quantum uncertainty (essentially tunneling) that they're able to get "over" that potential energy barrier and fuse. Man, I'd been reading everything I could get my hands on about both astronomy and quantum physics even since I was a little kid, but I had never heard that one before.
BenHead,
It is a fun calculation to do! A core temperature of 15,000,000 K means a mean energy of 1.3 keV per proton. But the distribution is Poisson, meaning that there is a small probability of having protons with extremely high energies. With 10^57 protons (of which maybe a few times 10^55 are in the core), I get the highest kinetic energy a proton is likely to have is about 170 MeV. This is almost (but not quite) enough energy to overcome the Coulomb barrier between protons.
But quantum overlap of wavefunctions at those high temperatures and pressures does in fact allow fusion to occur, at the furious rate of around 10^38 protons per second!
It is cool stuff; too bad that one can only write so much in a blog post.
This is the thing I don't get about the proton-proton chain: the inputs are 6 protons, the outputs are 4 protons and 2 neutrons plus a couple of neutrinos, positrons and gamma rays. Now neutrons have more mass than protons, positrons have electron-equivalent mass and neutrinos have non-zero mass. So how is this turning mass into energy, when the total mass of the products is higher than the mass of the 6 protons you start with?
This has been bugging me for a while.
@ Kym
It is the mass of the Helium. The output is not 4 free p and 2 free n, since 4 of those guys are now bound inside the Helium nucleus. Look up the mass of the Helium nucleus, and you will see that its mass is not the sum of the masses of the 4 constituents when they are free.
Hi Ethan,
The periodicity of the Cepheids is in the order of days to months.
Heat generated in a star's core takes _years_ to flow to the surface. (Since there is only conduction, no convection.)
Hence whatever the mechanism of Cepheid pulsation is, for sure it does not involve change of core temperature.
It must be some periodic chemistry in the upper layer of the Cepheid. Presumably some chemical equilibrium is sensitive to temperature, with one state having higher capacity for emitting radiation than the other state.
@Sascha Vongehr
Thank you. I've asked this question of a lot of people, so it's satisfying to finally get the answer.
Very excellent summary. I'll have to reread it again later.
I sort of knew this stuff but I really didn't. It's nice to have it all put together so clearly.
about 300 Watts per cubic meter, or the amount of body heat generated by two adult male humans
How many females in heat?
*ducks*
Cleon,
Thank you. I have updated the article, although now it's bothering me to not know, exactly, what causes these rapid pulsations at the surface if it isn't pulsations in the core!
Sascha,
Thanks for the quick explanation of nuclear fusion. One can only put so much in an article, and I regret omitting that bit of information. Thanks!
As to the mechanism of Cepheid pulsation.
According to the sources I consulted the first to surmise the nature of the mechanism was Eddington.
It had to be an opacity issue. The mechanism is named af the the usual letter for opacity: kappa.
The kappa-mechanism, or the k-mechanism.
Eddington had no way of pinpointing the precise molecules/ions involved, however. That came later.
The most extensive presentation of the k-mechanism I came across:
http://www.quantumweb.freeservers.com/cepheid/cep8.htm
I suppose the proposed chemistry of the k-mechanism is hard to verify. I suppose the scale is to big to replicate it in an experimental setup.
Information about energy transport from a star's core to the surface:
http://csep10.phys.utk.edu/astr162/lect/energy/transport.html
An estimate of how much time it takes for the radiation energy to travel from core to surface:
(Most estimates are wrong, which doesn't matter, as the value is of no practical use whatshowever. The first author is way off, and everybody copies from that first one without any thought.)
http://sunearthday.nasa.gov/2007/locations/ttt_sunlight.php
As you make your object more and more massive, it continues to shrink and shrink.
Obviously Jupiter has passed that threshold.
Has Saturn? As Saturn picks up minuscule amounts of space detritus - let's say just a fine trickle of hydrogen - does it grow or shrink?
Just how large (assuming a standard gas-giant mix of ingredients) can a planet get before it starts sacrificing volume for density?
I did some more digging.
A discussion by Eddington, published in 1917
http://adsabs.harvard.edu/abs/1917Obs....40..290E
Eddington mentions that the size periodicity and the brightness periodicity appear to be a quarter of a period out of phase.
That is, Eddington points out that an extremum in luminosity coincides with maximum speed of volume change.
I get the impression that the sheer kinetic energy of stellar mass moving inward/outward is a significant factor in the overall dynamics of Cepheid pulsation.
Really interesting astrophysics, those Cepheids.
Ethan,
> 13 times as massive as Jupiter -- or about 8% as massive as the Sun
Well Jupiter is 1047 less massive than the Sun so these numbers do not compute.
but 13 Jupiter masses is the threshold for deuterium burning but since there is so little D around this phase doesn't last long. 0.08 solar masses is the threshold for hydrogen burning that marks a "real star".
--Ned Wright
...
If you go right down to the lowest masses for hydrogen-burning stars, the radii get well into the planetary domain. The red dwarf star OGLE-TR-122b is only about 20% larger than Jupiter as estimated by transit observations, and another red dwarf VB 10 has an estimated radius pretty much the same as that of Jupiter.
Plus "red dwarf" is not a proper noun, unless perhaps you were referring to the TV series?
Why cepheids are variable
http://www.youtube.com/watch?v=X_3QAB3o4Vw
@Cleon-
Why is the time it takes energy to flow from the core to the surface relevant? The core could experience pulsations on the order of weeks which translates (after the appropriate years-long lag) to brightness pulsations on the order of weeks.
Or is it that the density of the core precludes it from such high-frequency pulsations?
Although watching the video and checking up on Wikipedia, it looks like this surface process is a better explanation than a core process.
Another dumbed down scientific article to amaze the masses with scientific wizardry and slight of language. Why not include the sun's corona in your density measurements and amaze us with the fact that the sun's energy output is no more than a string of Christmas lights and LED lights at that. The devil's in the details which are so consistently glossed over by you scientific writers. The most interesting thing is the Heisenberg comment. Yet you science writers expect us to just nod our unquestioning heads while you enjoy the light and keep us in the dark under your pile of stone tablets. Booooooo!
Sorry I was so hard on you, good article. I'm just angry at science writers in general.
Ralfcis,
You are always free to speak your mind on the comments here.
I try to provide a level of detail that is appropriate for a general audience but in-depth enough that other professional scientists (and I am one, too!) will find no fault with it.
But if you have a particular line of inquiry you'd like me to explore, feel free to leave a suggestion! As you can see, my readers -- as in this post -- are often the source of inspiration for what I write.
I understand there's a very fine line science writers have to tread. Too much knowledge alienates the ignorant and you're trying to convey your message in a way that alienates the least number of people. Science writers should change their view that their audience is not so much ignorant as interested. You've got us but the devil's in the details we're not privy to. Try using a method that New Scientist uses where it greys out more technical blocks and adds them at the end. Mathematical equations would still be banned from these blocks but I feel you guys talk in mathematical equations the same way the rest of us read english. Surely there's a way to translate what the math is saying into straight English.
I have so many obvious questions about the electron that I can't find any answers to. I can post them here tomorrow if you like.
@neal
I did encounter a name for a mechanism where pulsations feed back all the way to the core: epsilon-mechanism. However, I didn't encounter a description of a case where astrophysicists actually posited epsilon-mechanism as possible mechanism for an observed variability.
So, what can I figure out with general physics knowledge, but no specialized astrophysics knowledge? Let me just assume that pressure pulses _can_ make it all the way down to the core. We know the pressure in the core is vastly higher than near the surface. I suppose that a pressure change that near the surface halves/doubles the pressure is just the tiniest ripple down at core level.
Any _temperature_ effect of pulsation in nuclear fusion rate has no way of making it to the surface as pulses, which leaves effects of outward travelling _pressure_ pulses. Presumably such effects will simply dampen out.
As Eddington pointed out, to sustain the pulsation energy lost to damping must be replenished, so work must be done. To do work there must be not only change of pressure, but also change of temperature.
As Eddington pointed out, it's not that a Cepheid is at its most luminous when it at its largest diameter. A Cepheid is most luminous halfway during the shrinking part of its cycle. That makes sense: when translucency goes up there is opportunity to lose energy in the form of radiation. With loss of energy the Cepheid shrinks.
I wasn't previously aware how massive the Cepheid pulsations are. Usually the radius changes around 25 percent!
That was a good write up.
>>"Every single second, the Sun fuses six hundred million tonnes of hydrogen into helium!"
Out or curiosity, I wanted to understand the magnitude of the Sun's power. I mean, then Soviets made the great Tsar Bomb, the largest Thermonuclear Device with a yield of 50 Megatons of TNT! My question is:
a) What would be the Sun's yield, at the rate of 600 millon tonnes/sec?
b) What happens when Sun blows up completely like that Tsar Bomb? I mean, what would happen to life, planets etc? Based on the Newton's Law, our Solar System should cease to exist in such a dreadful scenario! Isn't it?
Do respond, thank you.
Only if the heavens above can be measured and the foundations of the earth below be searched out will I reject all the descendants of Israel.
@Cleon
There have been many cases where the epsilon-mechanism is posited as the dominant driving mechanism for a pulsating star. However, there are few in which that turns out to be the case.
There are two things to say here about the epsilon-mechanism:
First, how does it work? The epsilon-mechanism is jargon for something like a heat engine operating on oscillating material inside a star. We can think of oscillations in stars a few ways, but the most useful in this context is to think of them as temperature perturbations. That is, if I follow a piece of the star as it oscillates, it gets hotter and cooler as it moves. This is useful because the nuclear reactions (at least most of them) are *highly sensitive to temperature.* For typical Hydrogen fusion in the Sun, the burning rate is proportional to T^4 or so (though for the oscillations it's actually closer to T^10, but that's a longer story). So as my piece of star oscillates and changes its temperature the fusion rate responds in kind. So over the course of each oscillation, this additional fusion adds energy to our little piece of star driving the oscillation to even larger amplitude.
Second, why doesn't this *always* work for driving pulsations? Well, it does, but the problem is how hard it can drive them. And here, @cleon, you have already touched on the answer. For most stars, since the density changes so greatly from core to surface, the amplitude of the pulsation in the core is much much less than near the surface for most modes of oscillation. And since the epsilon-mechanism requires that fusion be able to act on the pulsation, if the amplitude is low where the fusion is happening, the epsilon-mechanism cannot have much effect.
However, in some stars, particularly the most massive ones just beginning to fuse hydrogen (so newborns), the density contrast is actually fairly moderate (relatively speaking). So in these cases, some oscillations can have a large amplitude near the core of the star, overlapping with the fusing core, and voila! You then have the possibility of substantial forcing by this epsilon-mechanism.
So given that, I return to statement that it has been posited in many cases, when the pulsations in stars have substantial amplitude where there is fusion, but in nearly all those cases, something else, usually the kappa-mechanism proves dominant. There are, though, some very interesting exceptions.
One interesting and recent example where the epsilon-mechanism is important can be found in the work of Alex Heger and Stan Woosley published just last year. In this work they show that the effect of nuclear burning on oscillations in the core of metal-free stars (as the first-generation of stars after the big bang are thought to be) can drive these oscillations to fairly large amplitudes. There are other stars where the epsilon-mechanism provides at least some significant contribution to driving, the first one that comes to mind is in young(-ish) white dwarfs, which have shells of burning stellar matter fairly near their surfaces. However, in at least some of these cases, the oscillations are not the radial ones that we've been implicitly discussing here, but instead are non-radial oscillations, which means they are not spherically symmetric (that is, it's not only in radius that things are moving). The discussion of these gets a bit more complicated, but if you're interested see cool movie of what these look like here and a great set of notes on the topic here.
Not only very informative, but also kind of inspirational. Like most of the things on Earth and the Solar System, we are a byproduct of the existence of the Sun. We feed on the Sun's energy (since photosynthesis is at the base of the food pyramid). And - if I get it right - we output roughly the same amount of energy per cubic meter as the Sun. I've never felt so connected with the Cosmos as I'm feeling now.
Thanks for the crowd image. Beautiful page!
Wow,this is the article I'm looking for,it helps to solve my doubts,thank you for sharing.
wowo wow!!!!!
Sorry about this; Not so bright when it comes to the sciences. How does the sun, or any star for that matter, produce energy/heat/fire without oxygen?
Simple Steve,
The sun's energy doesn't actually come from burning anything. It's not a fire that makes the sun hot. In fact, if the sun really were just a massive ball of hydrogen that was burning, it would have burned itself out millions of years ago. The sun's energy instead comes from nuclear reactions, namely a fusion reaction that converts hydrogen to helium. No oxygen is needed for this process.
i pruve that inside the sun very cool is their and the atraction betwen sun and other planet becuase of the oppasite praporty not only gravitastional force
Thank you very much for helping me out! But i'm not trying to be mean or anything but I couldn't understand that rest of it because I have a science project and I don't want it to seem as if i'm carbon copying everything they are saying because I'm going to put my links and their going to look at them and then their gonna be like wahhhh she's totally getting a c-! LAME! BUT THANK YOU GUYS SO MUCH FOR HELPING I REALLY APPRECIATE IT! ;)