"Summer ends, and Autumn comes, and he who would have it otherwise would have high tide always and a full moon every night." -Hal Borland
Of course you know the danger that would befall us if the Earth ever got too close to the Sun, as the Perry Bible Fellowship shows, atop. But have you ever stopped to think about the Moon in our skies, and what would happen if the Earth and Moon were closer together than they actually are?
While photos such as this -- from the Galileo spacecraft -- accurately show the relative size and illumination of the Earth and Moon, it's a trick of perspective that hides the actual vast distances between these two objects.
If I were to insist on showing you the Earth and Moon, including the Earth-Moon distance shown to scale, it would look very different!
The Moon is, on average, about thirty Earth-diameters away from our planet. This tremendous distance helps explain why the Moon appears to be the same size in our sky regardless of whether it appears directly overhead -- which it does close to midnight on the full Moon -- or on the horizon, when it's another full Earth-radius away.
But what would happen if the Moon weren't so (literally) astronomically far away from us?
In other words, what would happen if the Moon were closer to us?
Well, if the Moon were, say, only half the distance away from us as it is today, we would immediately notice a few large differences.
Yes, the Moon would appear twice as large in the sky, and yes, it would be about four times as bright due to its proximity. But that's not really a major change.
But there is something that would change majorly.
Right now, on Earth, the difference between high and low-tides affects the ocean height by a substantial amount. The Moon (and to a lesser, about 30% effect, the Sun) gravitationally pulls on the Earth slightly more strongly in the direction closest to it, and slightly less strongly in the direction farthest from it.
This causes the liquid part of the Earth -- the oceans -- to form two bulges, which are responsible for the high-and-low tides as the Earth rotates. This is why there are two high tides and two low tides each day; each point on the Earth needs to pass through both high points and both low points to make a complete rotation about its axis.
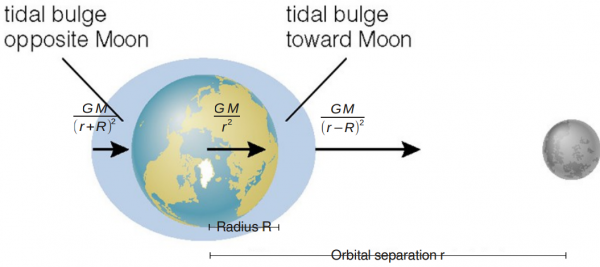
Image credit: Exploring the Cosmos, via http://exploringthecosmos.tumblr.com/.
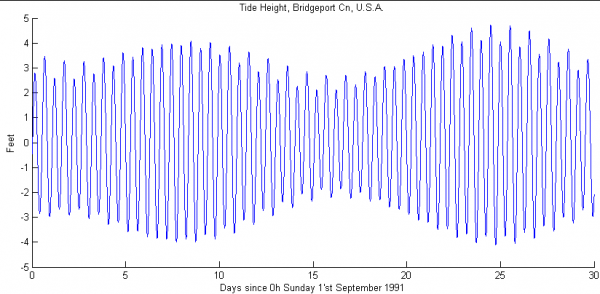
With the Moon at our current, 30-Earth-diameter distance, this means that the difference between high tide and low tide can be anywhere from about 5-to-8 feet (1.5 to 2.4 meters), depending on where the Sun, Moon and Earth are relative to one another. (Yes, there are other slight variations to do with latitude etc., but I'm ignoring those.)
But if the Moon were just half-the-distance it is to us now?
You might think that the difference between high and low tide would be twice as large. Or, you might remember that Newton's Law of Gravitation is an inverse-square-law force, and so you might think the tides would be four times as large.
The way tidal forces work, it turns out, means that the tides would be eight times as large as they are now, or that each day, the difference between high and low tides would be about 52 feet, or 16 meters.
In other words, every high tide would bring catastrophic worldwide tidal waves to coastal cities everywhere.
And if the Moon were only one-fourth the distance it is right now, those waves would be 400-footers instead of 50-footers.
And if you were willing to bring it a little closer -- just under one-eighth the current distance -- the Moon would pass through geostationary orbit, and would always appear at the same point in the Earth's sky.
Any closer than that, and the Moon would actually appear to rise in the West and set in the East, because it would be orbiting the Earth faster than the Earth itself could spin!
But things would get a whole lot worse for the Moon than they would for us. Because while the Moon's tidal forces on Earth can severely impact our oceans and coastal areas, the reverse -- the Earth's tidal forces on the Moon -- would begin to tear the Moon apart!
Only the core of the Moon -- because it's so much denser than the rest of the Moon -- would remain. And even that would only survive until the core was closer than about 2 Earth radii. And at that point, the tidal forces would tear apart even a solid ball of iron.
And if you dared to get much closer than that -- to low-Earth orbit -- you'd start to notice severe differences from the horizon to directly overhead.
An object orbiting maybe 200 kilometers (120 miles) above the Earth's surface would appear 10 times larger when it was directly overhead vs. when it first crested the horizon! This would apply to any rock, any component of a ring, anything at all, even our current satellites in orbit.
But 200 kilometers is closer above the surface than you'd ever want anything to be, because at that low-altitude, it will start to experience atmospheric drag. And once that becomes at all significant, you know what's next.
It will re-enter our atmosphere, moving at some five miles per second (8 km/sec), until the catastrophic heat from re-entry burns it up.
So be pleased about the Moon and -- like Rodrigo Andolfato -- make sure you enjoy tonight's Moon/Jupiter conjunction!
But be thankful that the Moon is as far away as it is, and resist the temptation to bring it closer and give it a hug. The consequences would be catastrophic for humans on Earth, but could be fatal to the existence of the Moon itself!











Cute analysis!
Katrina and Sandy would be nothing to compare then.
The moon at half its current distance from Earth was last experienced about 400 million years ago during the Silurian period.
The fossil record from that time shows that the lunar month lasted nine days of 21 hours so every ten hours or so conditions for surfing would have been quite spectacular on the coastal regions.
This post brought back fond memories of Ms Martin, one of my favourite and best HS teachers, who conducted a small series of natural history lessons on the theme: "Earth has been many Planets."
Of course, if the moon were in geostationary orbit, the number of tides per day would be...zero, right? So although sea level would be 400 feet higher at some points than at others, no given point would experience a periodic rise and fall of that - or any - amount.
Let's do it! :D
the difference between high tide and low tide can be anywhere from about 5-to-8 feet (1.5 to 2.4 meters)
Or more, depending on topography. According to Wikipedia, Burntcoat Head on the Bay of Fundy has normal tides of 17 meters, and another Canadian site, Leaf Basin on Ungava Bay, has normal tides of 16.8 meters. In the case of the Bay of Fundy, the interval between consecutive high tides matches the time required for a rising tide to travel from the mouth of the bay to the head, producing a resonance effect. Conversely, Florida with its relatively straight Atlantic coast has smaller tides (1 m or so, as I recall from growing up there).
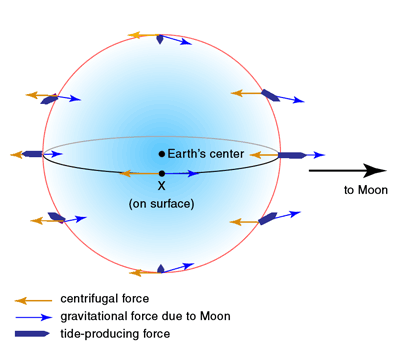
As is often forgotten, the high tide on the side of the Earth opposite the moon is also due to the Earth and Moon forming a couple as they orbit. Think of an off-center baton. Centrifugal force of the Earth spinning around the center of the couple helps cause the other high tide.
the moon-jupiter conjuction is really nice for naked eye observers and binoculars, but hot damn, at 98% illumination, that thing is searingly bright through even a small telescope.
Well this was a really interesting post.
So many things I didn't know, should've known, now know.
Nice. thanks.
Alan L
Thanks, Your comment sent me tracking this http://www.bbc.co.uk/news/science-environment-12311119
Coincidentally, at 5:40 am this morning, the moonlight was bright through the curtains. And Jupiter right there. I grabbed my iPad and turned on SkySafari (the free version is absolutely mind boggeling, I may never need the pay version) to check; yep that was Jupiter. But what about that bright star above to the right, oh Capella. Nice, a nearby binary star; SkySafari is my private tutor.
Now I really need to get those astronomical binoculars that Ethan keeps mentioning for myself for a Christmas present.
Hmm?
"NEVER hug the MOON"
Now, that's a double entendre if I ever heard one.
Greg23: there are far more wrong explanations out there for tides than there are good ones. Centrifugal force is a popular reason but is not accurate. The high tide on the "far" side of the Earth is caused by exactly the same effect as the high tide on the "near" side of the Earth - the differential pull of the Moon's gravity.
that first tide diagram with the centrifugal force is confusing. just how is the attractive force of the moon's gravity supposed to *push* the water away causing a tide? Joffan is right.
also: centrifugal force is not a real force. it is just a convenience to use when you find yourself doing physics in a non-inertial reference frame.
"just how is the attractive force of the moon’s gravity supposed to *push* the water away causing a tide? Joffan is right."
By being less than the centrifugal force that is in the away direction, with the vector addition of the two forces resulting in a force away from the surface.
"also: centrifugal force is not a real force. it is just a convenience to use when you find yourself doing physics in a non-inertial reference frame."
And there's no problem with doing so, and we are talking about such a frame, so what's your point? I mean nice factoid but we already know.
"This causes the liquid part of the Earth — the oceans — to form two bulges"
Not wanting to be picky, but it causes the *solid* part of the Earth to form two bulges as well.
If the earth tide were to increase 8 times, we would have a 3m earth tide occurring under us twice per day.
That could be just as interesting as 16m ocean tides.
I also want to take issue with the simplified explantation of the tides you have here - It pains me that no one understands that there are _far_ more than 2 bulges on the earth where the tide is high - see http://www.seafriends.org.nz/oceano/tides.htm for a reasonably good explanation.
The two bulges myth is one of those lies for children which appears to have gotten out of control, and I wish that every discussion of tide had some kind of disclaimer that this isn't the full story.
About the diagram credited to 'Naval Postgraduate School'.
Clearly, what the author of that diagram wanted to convey is a notion that the tidal effect is a resultant of two factors: one that is uniform for the entire Earth, and one that is a gradient over the width of the Earth.
The simplest case of tidal effect is the example of straight-fall-towards-a-small-black-hole-spaghettification. As pointed out by others, it's the gradient in gravity that does the spaghettifying.
Let's look at an object in the process of being spaghettified. In a diagram you can place vectors for the gravitational acceleration at points along the length of the object. To isolate the tidal effect you subtract from each gravity vector the amount of acceleration at the instantaneous center of mass of the object.
Using the object's center of mass as the zero point of the tidal effect is an arbitrary choice, it's just the symmetrical choice.
Something along that line was the intention of the author of the diagram. The orange vectors are all the same: same magnitude, same direction. The resultant vector of the oranges and blues is the tidal effect expressed relative to the Earth's center of mass.
But strangely the orange vectors are labeled 'centrifugal force'. Huh?!
The Earth and the Moon are orbiting their common center of mass.
So if you would want to represent a centrifugal effect arising from the Earth orbiting the center of mass of the Earth-Moon system then you get _different vectors at different positions_.
The orange vectors in the diagram are definitely not vectors for any centrifugal force someone might want to tie into the explanation. The orange vectors, being all the same magnitude and in the same direction, represent the gravitational acceleration of the Earth's center of mass. In the diagram the mislabeled orange vectors do not represent a force, they represent an abstract concept.
The image credited to 'Naval Postgraduate School' was (presumably) retrieved from this page:
http://www.oc.nps.edu/nom/day1/partc.html
The introduction to the overall course says it was last modified 31 march 2003
http://www.oc.nps.edu/nom/
Beautiful to see the analysis from a moons prospective.
While its true that the tidal force obeys a 3rd power law, and will increase eightfold if the distance between earth and moon is halved, i'm not sure if the same holds for the height of the tidal bulge. My first guess would be that the water surface is aligned along a surface of equal potential energy, which I think would follow an inverse square law at its maxima.
Of course, i'm writing this on the train and don't have pen and paper nearby, so I might be completely wrong.
I am one of those rascals who told my high-schoolers that there would be two high tides a day. I also told them that as soon as the land masses get in the way, and the moon moves things get more complicated. I live on the East Coast at the bottom of the Gulf of Maine, so we get to discuss the period of a standing wave in the ocean and the effect of the funnel known as the Bay of Fundy. Where I live a 10 mile drive takes you from a place with a tide range of 1.5 ft to a place with a range of 9 ft.
I was also lucky as a high school kid to be on a boat to see a total eclipse of the sun on March 7, 1970 off Monomoy Island. The Moon was a bfd in those days.
Just wanted to mention that seeing a PBF comic on the blog was a real treat.
Ethan:
Garth W is correct that there aren't two bulges of water. However, his link provides a rather incomplete treatment.
In particular, your statement that "This causes the liquid part of the Earth — the oceans — to form two bulges, which are responsible for the high-and-low tides as the Earth rotate" is not correct. There is a "bulge" formed by the force (as you show), but this forcing does *not* create bulges of water. http://www.lhup.edu/~dsimanek/scenario/tides.htm has a more complete treatment.
Sam K:
Your link is really interesting and gives the best explanation I've yet seen of the forces involved. It's interesting to me that the whole thing still has only diagrams of the two bulge model, and mentions the way that tides in individual oceans are reinforced waves only in passing. I guess it is correct that it is a really deep and complicated subject!
Garth W:
it is indeed a rather complicated subject. My main issue with the seafriends website is that it makes essentially the same mistake that the bad textbook explanations do-- it assumes that the majority of the tidal effect is from the "bulges of water" as opposed to the "bulges of force." The tractive component of Laplace's tidal differential equations (known since the 1770s and Kelvin waves known since the 1860s) is what creates the larger tides on the shores. It is not a "new model" by any stretch of the imagination. The listed "problems" of the "old model" are merely misconceptions of the author. The last in particular is telling (the bulge on the opposite side is hard to explain).
Not surprisingly, they cite no specific sources relevant to their explanation (except for the Poseidon data).
I have a question about some old SF trope related to this: The twin planet.
Last year there was some movie about a second Earth and Moon appearing in our skies. They were close enough for both to be visible during the day. A cool image, but I assume that's close enough to knock both planets out of a stable orbit.
So, how far away would a twin planet have to be in order for both to enjoy a long happy life spinning around the sun?
William the answer to your question is "depends on how long they need to be observed as stable".
And answering that is merely look at the strength of gravitational attraction between the two earths (at closest approach) and if it's less than Jupiter's effect, then you can consider it uninvolving.
Sam, George, I think you both need to clear up your nomenclature.
The height of the tides has almost nothing to do with the height of the bulge that the gravitational pull of the moon has on things. Look at tidal bores. The biggest difference is the shape of the land when it comes to landfall of the tidal bulge.
However, without any bulge at all, there would be no tideal bore, since there would be no swell to concentrate into a higher deviation in the estuary.
So if you talk about the height of the tides ON THE SHORELINE, you would reach a different conclusion about what the proximal event causes the height of the tides compated to what is the primal cause.
Secondly, most of the deviation of the sea level above "average" (i.e. the shape it would have absent the moon and sun) is caused by the moon forcing the water to one side, NOT by lifting it up (if it were, then you would have one bulge on the moonward side and one dip on the opposite side). For much the same reason as you get Lagrange points around the earth-sun system (within one of which we have a trailing moonlet).
Wow:
I guess I wasn't clear. I don't think we disagree, but I'm not sure where you think I said that the height of the "net force bulge" at a particular location has much to do with the tides on the shorelines near that location. That would only be true in an equilibrium state.
My [implied] point about shorelines was that you'd need to solve the differential equations *for a particular land shape* to get the actual tidal effect, i.e. the "force bulge" doesn't predict tides on the shorelines to any degree of accuracy.
I really enjoyed reading this article, am gonna think twice before wanting to hug the moon now xD
Sam, the problem is I think in that one is talking about the tides in the ocean (which would be the tidal bulge) and one is talking about the tidal range (which is at the shoreline). With a few others adding in local gravitational anomalies, subsurface swells (not caused by gravity) and so on.
But people are lumping them into "the height of the tides".
So as one is saying "you're wrong", the one they are saying it to know that is not true. Because they are both thinking of different things.