There are a few questions that have perplexed humans for all of recorded history, ranging from the nature of matter to the origin of the Universe to whether there are limits to what is knowable in principle about all there is. One of the great questions that people have wondered about since ancient times -- that we still wonder about today -- is whether there's a fundamental smallest scale to the Universe or not.
From the ancient paradoxa posed by Zeno to Heisenberg's uncertainty principle, it might seem like there either could or couldn't be a fundamentally smallest scale; maybe the uncertainty in measurement is just our uncertainty, and maybe isn't inherent to the Universe at all. Or maybe it is fundamental, after all.
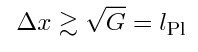 Image credit: A generalized uncertainty relation, via http://4.bp.blogspot.com/-jLtyTEMrKpQ/Tx_e2sF0sCI/AAAAAAAABIE/D1UbRkRcK….
Image credit: A generalized uncertainty relation, via http://4.bp.blogspot.com/-jLtyTEMrKpQ/Tx_e2sF0sCI/AAAAAAAABIE/D1UbRkRcK….
An outstanding exploration of the smallest possible scale from Sabine Hossenfelder; go read the whole thing!


Very nice post!! I was meaning to ask for a post about minimal length for a while now :) Someone out there is psychic.
In my mind, the proposal of Loop Quantum Gravity, that the area defined by 2 particle pair popping in and out of existance is a quanta of spacetime, is quite elegant. There is of course no reason (to my knowledge) why it should be the minimum. But if we look at nature to point us, it does seem plausible.
If there is a smallest possible scale, would that mean that there is a shortest possible time (Planck’s time??). If that is so, does that imply that time does not progress. If such a “quantum of time” had length, nothing could progress through it, nor could it progress past a given point, because nothing could ever be half way through it. If it does not have length, it is a time interval of no duration which as Peter Lynds points out, cannot exist.
@Bill S: Your attempt at reductio ad absurdum is self-contradictory. Your comment about "nothing could ever be half way through it" implicitly assumes that time is continuous, which contradicts your hypothesis that time is quantized.
If time is quantized (as some theories of quantum gravity suggest), then nothing would ever be "half way" through that minimum interval. Rather, time would proceed in jumps from one interval to the next. This is quite analogous to something you might be more familiar with: energy levels in atoms. Electrons transition from one level (orbital) to another in pure, discrete steps, not in continuous motion.
@Bill S: Read the book. There is a chapter there on exactly the kind of a priori (question begging) arguments against discreteness you are making here...
I don't understand this complaint about the title of the book:
"My only complaint about the book is its title, because the question of 'discrete vs. continuous' is not the same as the question of 'finite vs. infinite resolution.' One can have a continuous structure and yet be unable to resolve it beyond some limit, such as would be the case when the limit makes itself noticeable as a blur rather than a discretization. On the other hand, one can have a discrete structure that does not prevent arbitrarily sharp resolution, which can happen when localization on a single base-point of the discrete structure is possible."
The only way to determine if a quantity appears blurred due to uncertainty of measurement or due to the fact that the quantity is fundamentally discretized is to measure it more accurately. E.g. we know that the electron energy in atoms is discretized because the step changes observed are larger than the smallest step changes in energy that we can measure. Similarly, we know that The Mona Lisa, by Sanghyuk Moon image has been discretized during the image capture and/or rendition process because we have higher resolution devices to prove it — and common sense tells us that the painter could not have painted a precisely pixellated image with very clear and uniform step changes at the borders of each pixel.
Now, the only reason that the depicted Mona Lisa image appears pixelated, rather than blurred, is because the discretized data has been transferred directly to the continuous analog domain: bypassing the mathematically required discretized-to-continuous domain reconstruction filters. Such filters remove frequency energy (spatial detail in this case) higher than that of the original sampling frequency. Mathematically, the discretized domain is very different from the continuous analogue domain — this fact is often forgotten when analysing, say, tables of data and pixelated images.
If (some/all) fundamental properties of the universe are discretized then we are in error each time we convert them into the continuous analog domain — this error will manifest as blur.
Note: I'm not talking about Heisenberg's uncertainty principle; I'm talking about the fundamental acquisition, representation, interpretation, and analysis of data, and my failure to understand why the author of the article complained about the title of the book.
There is a strange relationship purely geometric relative to black holes. The mass of a black hole can be determined in function of its Schwarzschild radius (r_s) as follows:
[1] M = 1/2 DP r_s lp ^ 2
where
dp = density of Planck
lp=Planck length
It’s trivial to prove that the equation [1] is equivalent to the classic equation M = r_s c ^ 2 / 2G.
The advantage to rewrite the equation as in [1] is that it can easily be seen as the product of lp^2 r_s has the size of a volume and therefore we can reduce the equation to a sphere placing 2M / dp = 4/3 π r ^ 3
solving r (r_n) we get:
r_n=sqrt3(3M / dp 2π) = sqrt3 (3M ħ G^2 / c^5 2π)
From the analysis of the equation we see that the size of the radius calculated is really tiny. the value of the ratio (constant) ħ G^2 / c^5 2π is in fact equal 9.258^-98 m^3 kg^-1.
Being the mass below the cube root, the function grows very slowly with increasing of M.
To realize how tiny it is, if we calculate r_n of a black hole with a mass equal to the mass of our universe that we get r_n=10^-14 meters.
The equations r_s = 2GM / c^2 and r_n = sqrt3 (3M ħ G^2 / c^5 2π) are thus both a mathematically correct representation of a black hole, but only for first one we know how to give a precise physical meaning (Schwarzschild radius).
However, since the size of r_n become so tiny, we can only assume that it represents the minimum size mathematically possible of a black hole singularity.
In other words, we could say that the equation seems to suggest that the maximum density that matter can take in nature is equal to half the density of Planck, since by [1] we obtain that the relationship between black hole mass and the volume lp^2 X r_s is:
M / r_s lp^2 = 1/2 dp.
As there is no theoretical limit on the maximum size of a black hole, then becomes interesting to study the functions for very small values of M and see how r_s and r_n vary depending on the size.
The most immediate and easy to be calculated is for what values of M is equal r_s to r_n.
Let us then
2GM / c^2 = sqrt3(3M ħ G^2 / c^5 2π) and solving for M we get: M = + / - sqrt (3 ħc / 16πG).
The mass must be equal to 5,32x10^-9 kg (approximately 1/4 of the Planck mass).
To get r_s and r_n then multiply sqrt (3 ħc / 16πG) x (2G /c^2) = sqrt (3 ħ g / 4πc^3) = 7,90x10^-36 meters.
The solution tells us two interesting things:
The value of r_s and r_n are less than the Planck length;
For mass values < sqrt (3 ħc / 16πG) and that is about 5,32x10^-9 kg r_n becomes larger than r_s! In other words, r_s that is the event horizon of a black hole, an ideal surface purely mathematical, it becomes smaller component of the physics of matter collapsed into a singularity. The center of mass of the sphere ideal of a black hole passes outside the event horizon, the 'black hole' becomes a 'white hole', the matter explodes outside. Internal and external exchange of role!
@Michael Kelsey: “Rather, time would proceed in jumps from one interval to the next. This is quite analogous to something you might be more familiar with: energy levels in atoms. Electrons transition from one level (orbital) to another in pure, discrete steps, not in continuous motion.”
The electron moves in discrete steps because the energy is quantized (?). As far as I am aware, there is no question that it is the electron that does the moving. For the situation with time to be analogous, quantized time would have to be static, with everything moving through it in discrete steps.
This is why I asked the question: “does that [the existence of quanta of time] imply that time does not progress?”
Would quantized time necessarily be static?
@Bill S: Ah! I guess that I didn't quite understand your comment. Our best understanding of nature, based on relativity and quantum mechanics is that time is a _dimension_. That is, time "itself" is exactly a static measuring stick: when we perceive time "flowing" (as Newton wrote), what we understand is "really happening" is that we are moving along that static dimension, seeing different "slices" of four dimensional spacetime as we go.
Obviously there are a whole host of philosophical questions related to this, which this margin is too small to contain ( :-) ).
Putting aside that philosophy, the question of continuous vs. quantized time becomes much simpler: In classical relativity, the time dimension is continuous (like the real numbers) and we move along it in "steps" of infinitesimal dt's. If time is quantized, then the time dimension is discrete (like the integers), and we move along it in steps with some finite size delta-t.
Of course, those theories (various versions of quantum gravity) have that delta-t being so small as to be essentially immeasurable, and certainly imperceptible.
@ Michael & Bill
Time is the ultimate brain teaser IMO. After much search and deliberation, I came to agree with Leibniz and Kant that time is not physically real. Everything we ascribe to time is either emergent or product of our own reason. Thus the answer to weather it is discrete or continuous will come from the framework we use to describe it.
The simplest explanation why I think time is not fundamental, comes from thinking what time actually is and how it is measured. One of the simplest answers comes as a statement that "time is a measure of change", taken in it's most general sense, we can see that this measurement is immediately tied to something a priori that does this changing. If there is nothing to change or even nothing to be, there is no time to be kept or measured. Other way to paint this would be to say that if nothing moves, there is no time.
This leads to how we measure time.. a move of a dial, an oscillation of an atom or anything else. Something changes from point A to point B. That delta is what we think of time.
This then leads to relativity and QM... One might be tempted to say that relativity showed time is real, just like space.. it changes, contracts etc.. But this is an illusion. Yes, space contracts, and if time is a measure of change in position or momentum or whatever property, if that property changes, if that metric you picked starts changing, it's only natural that rate of change will change as well. Thus clocks will move faster or slower. But it's not some "real" time that changes... no.. the movement of all those atoms in their refference frames changes..depending on the speed of that lump of metal we call "clock". We accelerated atoms, thus changing their movement. That we equate a total of some motions to be something we call "seconds"... is s convention.. it's not an entity on itself. Yes, it is a mathematical dimension... a fancy was of saying it's a line where we humans draw little numbers... It's not "out there" existing on it's own, like i.e. Mercury does.
Lastly we come to QM. And given the previous train of thought (which of course might be completely wrong), I hope it's easy to see, that in QM time has to be quantized. If all change happens in discrete blocks, and there is a minimum for that block, then our measure of change will be in blocks as well, based on same minimum that change has to abide by.
This is all fine as speculation and philosophy, so what about the Universe we live in. Couple of things.
- since universe already has energy/matter content that is, a priori from us, in a state of motion, our universe has "time" because change is measurable.
- The only way to stop time would be to put the whole universe to a state of absolute 0, which can't be done in any number of finite steps. (tied to next step)
- since QFT tells us that even at the smallest possible scales, you will have fluctuations, which are nothing else than changes, in laymen terms we can say the Universe was "born" with time, but it's not a structure on itself, it's just motion.. a change in energy... That energy change is real.. our measure of seconds is our own.
Am sorry for a longer post than usual. Just wanted to get this of my chest :) And was maybe hoping that this topic on scale and limits of would sprout a more fruitful debate.
I never liked the convergence of infinite series idea because the series never gets to infinite. The solution I support is the idea that there is a smallest length,
@James Briggs #10: Your first sentence doesn't seem to make sense. If a series _converges_, that means that, no matter how many terms are included (i.e., in the limit of N -> +infinity) the sum remains finite, and indeed has a fixed value. If the series itself does not have such a finite limit, then we say it _diverges_.
In physics, a divergent series is generally an indication that the physics we have included is missing something, or we are applying the physics outside of its domain of validity.
@James Briggs #10: Your first sentence makes sense to me, but I don't understand the solution you support in your second sentence. Please elaborate.
An exciting and challenging discussion. I have been working on a "universal design" conception composed of concave dimensions formed by densely-packed spheres, whereby electromagnetic waves fluctuate in time as they pulse through concave fractal spaces. The model relies on the notion of a finite small space, and can be, I think determined through a reliance on calculating limits; Planck's constant works well for this. I say "I think" because I'm only an amateur who works in the area of thought experiments, not complex mathematics. I wish i lived somewhere where I could engage better minds on this and similar subjects.