“Never erase your past. It shapes who you are today and will help you to be the person you’ll be tomorrow.” -Ziad K. Abdelnour
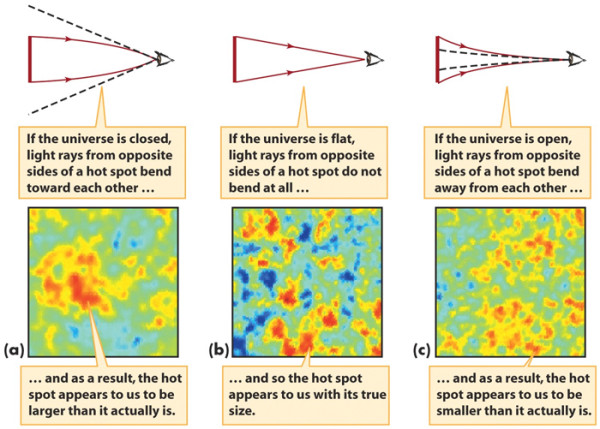
But even moreso than the fact that we're shaped by our past, the Universe itself -- geometrically -- is shaped by its history and composition. You might imagine all sorts of possibilities for how the Universe could have been shaped: positively curved like a higher-dimensional sphere, negatively curved like a higher-dimensional saddle, folded back on itself like a donut/torus, or spatially flat on the largest scales, like a giant Cartesian grid.
Yet only one of these possibilities matches up with our observations, something we can probe simply by using our knowledge of how light travels in both flat and curved space, and measuring the CMB, the source of the most distant light in the Universe. The result?
A Universe that's so incredibly flat, it's indistinguishable from perfection. Go get the whole story for this week's Ask Ethan!


How space can be perfectly flat and at the time of the big bang have had a finite size.
1. The speed of expansion approached infinity, but continuously so fast that space is infinite now
2. Some sort of discontinuous phase shift where space instantly goes from finite (with a possible positive curvature) to infinite in size and flat. Like a balloon breaking. I find that counter intuitive.
Is it possible to rule these out?
It is possible to be flat and finite in size without some kind of edge?
@Erik
We'll, using a balloon, one can see how an infinite object can have a finite surface.
We'd then have to ask, what does infinity mean? Is eternal a better descriptive word?
I don't follow how you can have a universe whose size in light years is larger than the age of the universe. Eg: this image, courtesey of E. Siegel, based on an original by Wikimedia Commons user Azcolvin429 (https://d262ilb51hltx0.cloudfront.net/max/1274/1*eJzRFy2S6j9o46p7BW_lHQ…). What am I understanding wrong? Have I been had by Wikipedia? Is the universe riddled with folded space?
I thought there was no such thing as infinity?
So this basically just means we live in a 3D universe not a universe with more Ds because you would need a universe with more Ds for the 3Ds to bend in.
@Erik Martino Hansen #1: It sounds like you've somewhat misinterpreted the current inflationary model. We don't have any way of knowing how big, or even what topology, space was before inflation. The idea is that some _patch_ of that space (maybe the whole thing, maybe just a small bit), expanded exponentially for some period of time, expanding by at least e^60 times (60 "e-foldings"). When that inflation stopped, _whatever_ shape the patch of space originally had would have been stretched so far that, to us, it would appear to be flat.
The issue is simply one of scale. Look around your house, look around your neighborhood. The floor looks perfectly flat, doesn't it? The grassy park down the street, where kids play football, looks perfectly flat. But we know that in reality, that grassy park is a small section of a very, very, *very* large sphere. On a _local_ scale, you can approximate bits of that sphere as flat planes.
We don't know whether "space" (the larger system of which our whole observable universe is a part) is finite or infinite. We don't know whether it has an edge, or is a closed, unbounded surface. The inflationary hypothesis is close to your option (1): The expansion rate was so fast that an initially tiny patch could grow immensely in a very short time. The consequence is that our observations correspond to a tiny patch of that tiny patch, so we don't know about what's "outside."
We do know (observationally) that our observable universe, currently 46 billion light years in radius, is at least five times larger than that (if it were smaller, there would be observable features in the CMB). We know that it is not a closed flat surface (like a torus), because we do not have observations of repeated structures in the CMB (that is, we aren't seeing "all the way around" the Universe multiple times).
@Name* #5: Not true. There is no requirement for addtional dimensions in order to have a non-unit metric. Proving this is beyond the scope of blog comments (I recommend a good first-year graduate text on differential geometry).
What you _do_ need additional dimensions for, is if you want to try to draw a picture of what a curved space "would look like". That is called an "embedding diagram" (look it up), and is only a representational aid, not reality.
@Chris #3: You haven't been had. You've just been misled by multiple different definitions of distance; this is something Ethan has covered before. The oft-quoted "the universe is 46 billion light years in radius" (I wrote it myself at #6) is a statement of how large the Universe is _today_, as a result of expansion.
Suppose we take the very simple, old-fashioned view that the Universe has expanded at a constant rate, starting from a singular point some 13.8 billion years ago. Light emitted right after that expansion started would take time to reach its destination (us, in this case). But the source of that light has continued to be carried along by the expansion for all that time. You can legitimately ask, "How far away is that source from us, _right_now_?" The answer is 46 billion light years.
Size of the universe. Consider how flat the universe we see is. From the scientific laws we know, consider how un-flat the universe "ought" to be, given the constraints and the lack of constraint on uniformity.
How small a section of that lumpy material could on average be sampled and give the observed flatness?
NOTE: This is how you can get a better optical telescope too: Aperture reduction. A large mirror will on general, for more effort, therefore expense, be as good a shape as a smaller mirror. But due to variations, some places will be more correct than others. Cover the mirror and leave a hole, move the hole until the light that gets through hits a spot that is better than the average of that larger mirror. That selected area will be a BETTER quality than if you'd saved money and bought a telescope with an aperture the same size as the hole you used.
Likewise, some subset selection of what the universe "should" be will look like the flat shape we see. Therefore we can estimate that our universe we see is merely that small selection of the larger whole.
Thereby estimating the size of the non-visible universe.
To clarify Michael's point. His "right now" is a "now" defined as "Stop the universe entirely, then move out with a long tape measure and mark the distance traveled to that spot you looked at and saw the light from."
If you were to try to do that without stopping the universe, then the obejct is being carried away on its patch of space. That would be another definition of how distant that thing is: how far would you have to go to get there if you started off right now, as a minimum? I.e. at light speed, or so close as makes no odds..It is also the distance that it will be by the time we can notice any change in the object that occurred *now* here in our frame of reference.
Or the "right now" that you get when you look at the distance figures in your astronomical atlas: how far did that light coming from that object travel?
When things are moving, distance has multiple meaning.
This is no different than when you're shooting things moving, such as clay pigeon shooting. The clay may be right there "now", but if you want to shoot it now, you have to aim *somewhere else*, and that's the distance it is for working out if you have the range to hit it.
It does bring up a thought: what's the size of the REACHABLE universe?
The bit we could reach if we had interstellar travel at near light speed.
@ Wow# 10
"This is no different than when you’re shooting things moving, such as clay pigeon shooting. The clay may be right there “now”, but if you want to shoot it now, you have to aim *somewhere else*
EXACTOly Incorrect:
http://www.dailymail.co.uk/news/article-2876120/Department-Defense-test…
Scroll to the bottom of the article for the video.
But in fairness I see your point.
Ah, right. Well known for their scientific accuracy, the Daily Mail.
Article number 87 finally cleared up the shape of the universe for me. Great article got me thinking. We may never know the true shape because of the limitation of light
The Universe is flat. Check. This means that its density is exactly the "critical density". But as the Universe expands, the density of matter decreases while the density of dark energy remains the same. So the density of the Universe is decreasing.
Does that mean the curvature of the Universe is changing -- that it's tending toward open?
Or, conversely: ultimately, the density of dark energy will swamp that of matter and the Universe will essentially be exactly at the density of dark energy. Will the Universe still, then, be flat? Does that mean that the density of dark energy is *exactly* the "critical density"?
@Simplicio #15: "So the density of the Universe is decreasing.
Does that mean the curvature of the Universe is changing — that it’s tending toward open?" Apparently not. Something Ethan wrote about recently is that in a strictly matter+radiation Universe, the density, curvature, and evolution are fully correlated, as you understand it.
However, the addition of dark energy means that the evolution isn't correlated with the curvature: Dark energy can drive an accelerating expansion even while the curvature remains flat the entire time.
Thanks for answering my question. You said: "... evolution isn't correlated with curvature ...", which leaves open the question of what *determines* the curvature -- is it just matter+radiation (with radiation insignificant at the current epoch), with dark matter not contributing to the curvature (else how could the curvature be unchanging as dark matter predominates)?
Sorry! In the context of cosmological shape, dark matter has gone from being a separate hypothesis to being included by assumption under "matter" (vs. radiation, vs. dark energy). So when I wrote "a strictly matter+radiation Universe", I was including dark matter in that description, without saying so.
No, I'm an idiot (I've chosen an apropos screen name) -- I wrote "dark matter" instead of "dark energy" (doubtless because I'm also involved in a thread elsewhere). Let me ask a clearer and more direct question: What determines the curvature of the Universe? Apparently, it's not the energy density (as I would naively have expected), because the Universe is said to remain flat as future expansion causes dark energy to dilute the matter content to insignificance.
@Simplicio: My understanding is that the curvature _is_ determined by the energy density: the total energy density including matter, radiation and dark energy/quintessence/cosmological constant/gremlins/whatever :-)
The _evolution_, however, is determined not by the curvature, but by the "equation of state," the relationship between density and pressure. Here pressure is in a cosmological context, such that "positive pressure" induces a contraction of spacetime, while negative pressure drives an expansion. Both matter and radiation have w = p/rho > 0, which is why in a matter or radiation dominated Universe, the initially set expansion will slow down over time. But dark energy has w < 0 (the cosmological constant has w = -1), which causes it to drive an increasing expansion, in opposition to the slowing from matter and radiation.
Thank you once again. "... the curvature _is_ determined by the energy density ..." That's what I thought, too. But the energy density is changing as the current 70% dark energy + 30% matter (approx) goes to 100% dark energy as the Universe expands and the matter density is diluted to zero. Yet the curvature is said to be flat now and to remain flat. I'm missing something here.
"Yet the curvature is said to be flat now and to remain flat."
No, what Michael has told you several times now is that it won't REMAIN flat because we have dark energy which gives it a negatively moving curvature with time.
If we'd had enough to close the universe, that dark energy factor may have been enough to change that with time. If that turned out to be infinite time, then that would mean "going asymptotically flat".
Where do you get the idea it will always remain flat?
"Where do you get the idea that it will always remain flat?" See the last sentence of Michael Kelsey's posting #16. If I've been misunderstanding his reply to my original question, I certainly apologize.
My original question was whether dark energy is driving the Universe from flat to open; I'm just trying to understand the relationship between energy density and curvature in a universe with changing energy density and a dark-energy driven acceleration.
@Wow #22: My understanding may be incorrect; hopefully Ethan or some other theoretical astrophysicist will step in to correct me.
As I understand it, the simplest version of dark energy (equivalent to Einstein's big Lambda cosmological constant) has a special property: as the matter+radiation is diluted by the accelerated expansion, the _total_ density including dark energy is such to keep the Universe exactly flat at all times.
So even though the expansion is accelerating (in the same sort of way it might in an "open" Universe), the _geometry_ remains flat even into the future.
As I say, this is my understanding of the situation when Lambda is added to the LFRW metric. But I am _not_ a cosmologist, so it's quite possible for me to be mistaken.
@ Wow & Michael et all..
I'm not a cosmologist, nor a particle physicist, nor an astronomer :) ..
And would like to know the correct answer as well.
As far as my understanding, the "shape" of the universe is nothing more than talking about overall gravitational energy of the universe. Shape meaning the curvature of spacetime for the entire observable universe. If the shape is exactly flat, that means the overall gravity is close to zero. If the shape was positively curved, it would mean that gravity is taking over, expansion slowing and universe would start contracting. Given the accelerated expansion, and if that trend continues, IMO that would imply a negatively curved universe in the future? no? (there would be regions with positive curvature's which would correspond to regions with dense matter concentration, but overall it would be negatively cruved (anti-de sitter)..
"But I am _not_ a cosmologist, so it’s quite possible for me to be mistaken."
It's probably better to leave it to someone actively working in the situation, then.
p.s.
a correction of my #25 under more scrutiny.
The last part should be: De Sitter space.. not anti-de sitter..
while it is negative gravity, it's actually +1 in de sitter model..
-1 (anti-desitter) is for attractive lambda, not repulsive.
my bad.. ah those +/- signs..
When you only have a hammer, every problem looks like a nail. Ethan only has GR, so every problem looks curved in some way. GR is not the solution, GR is the problem. There is absolutely no way to construct a flat universe using it. Well, to be specific, there one way it could be flat but the odds are so long that picking a Megabucks number would look like a sure thing next to picking the right critical density for a flat universe.
Ethan likes to talk about the beauty of Inflation: how it predicts a flat universe, isotropy, quantum fluctuations in the CMB, etc. but all these problems that Inflation 'solves' were caused by GR in the first place. Inflation is nothing more than an ad hoc attempt to patch up a theory that failed to match observations.
"GR is not the solution, GR is the problem. "
When all you have is a complaint against hammers, everything becomes the wrong sort of hammer.
"There is absolutely no way to construct a flat universe using it. "
Nope, it's entirely possible. Indeed far enough from matter or in certain positions between masses, you get flat spacetimes no problem.
But I have to ask, why is that a problem? Nothing says that we have to have a flat universe or the theory is wrong.
"but all these problems that Inflation ‘solves’ were caused by GR in the first place"
No they weren't.
" Inflation is nothing more than an ad hoc attempt to patch up a theory that failed to match observations."
Wrong again.