"If you look for truth, you may find comfort in the end; if you look for comfort you will not get either comfort or truth only soft soap and wishful thinking to begin, and in the end, despair." -C. S. Lewis
And yet, when you search for the truth, you often find answers that butt up against your sensibilities, your preconceptions, and even your very notions of common sense. Such is the case in this week's Ask Ethan, where longtime reader and commenter MandoZink asks:
I have a question that has perplexed me for most of my life. Recently I sought out and re-read more expert explanations of the non-existence of a "center-of-the-universe". [...] But as a person with a very firm grasp of geometry (my career was drafting) I cannot conceive of a volume that would lack a central geometric point. Even if space is constantly expanding, a snapshot of the universe at any one instant would contain a center of volume. [...] I have not accepted this "no center" concept since the original and inadequate "stretching balloon surface" analogy. I would like a competent explanation that i can grasp. I do not care how in-depth it is, as long as it is not simply a "it doesn't exist" explanation.
So let's get to it: what's the deal with the geometry of the Universe, and whether (or not) there's a center?
 Image credit: Tim Phelan of http://acrosstheuniverseinnotime.com/.
Image credit: Tim Phelan of http://acrosstheuniverseinnotime.com/.
First off, it's important to draw a distinction between what we know as "our Universe" -- or what I'll call the observable Universe -- and "the Universe", which includes everything that's ever been connected to us since the Big Bang and a lot more. When we look out into the abyss of a dark, night sky, past the Solar System, beyond the stars, gas and dust in our own galaxy, out beyond our local galactic neighbors and into the vast void of what seems like eternity, that's us peering at our observable Universe.
We can look beyond the farthest observable galaxy, back to before the first stars formed, all the way back to the Universe's dark ages. Before even that, some 13.8 billion years ago, when the Universe was smaller, hotter and denser, it was too hot to form neutral atoms, and so it's this location that we see the relic cosmic microwave background (CMB) radiation. It's just a short 380,000 years before that to the moment of the Big Bang, or the creation of the hot, dense, expanding and cooling state that describes our Universe and all the matter-and-radiation in it.
That's our observable Universe, as visible from our location in space. The part that we can see is -- to an excellent approximation -- spherical, and about 46 billion light-years in radius, centered on us.
But that doesn't mean we're at the center of the Universe. Quite to the contrary, when we talk about the Universe, we have to talk about it in the context of the physical theory that describes it on its largest scales: general relativity. And relativity tells us that space isn't flat, like a 3D grid, but rather curved by the presence of matter and energy.
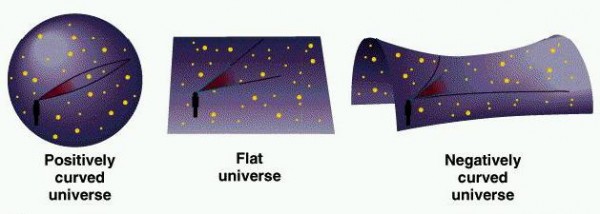
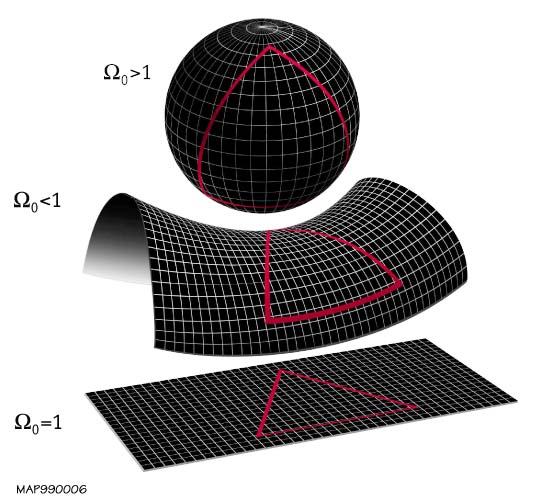
On the largest scales -- as in, on a global scale -- there's also the opportunity for the Universe to have curvature, depending on all the relative components of the different types of matter and energy and the Universe's expansion rate. It could either be negatively curved -- where the angles connecting any three points add up to less than 180 degrees -- positively curved -- where they add up to more than 180 degrees -- or flat, like the 3D analogue of a piece of paper, where the angles add up to exactly 180 degrees.
These curvatures also cause two lines to either converge, diverge, or remain at the same relative angle to one another as they proceed ever farther away.
Based on the best observations of our Universe coupled with our understanding of the physics governing it, we've not only been able to conclude that the Universe is flat to within our best error bars (and they're only on the order of 1%), but that the size of the unobservable Universe is somewhere on the order of at least 150 times bigger than the part we can observe. The best observations leading us to this conclusion come from the CMB.
The way we see the Universe at our location in space, assuming our physical understanding of the Universe is valid, is no different on the largest scales than any other observer at any other location would see it.
Yes, there'd be differences on small scales, as far as how grouped together galaxies were and local distributions and flows of matter. Some directions will have great clusters of galaxies while others will have great voids; some spots in the CMB will be hotter or colder in some directions than average. And these particulars will be inconsistent for observers located at different points in space.
But on the largest scales, any observer would find a Universe that looked roughly like the map you see, below. While the portion that any observer can see is always going to be a sphere (of radius defined by the light-travel-distance since the Big Bang) centered on that point, space -- in all three dimensions -- just appears to go on and on, with more Universe in whatever direction you try and perceive.
But what about the whole "center" thing?
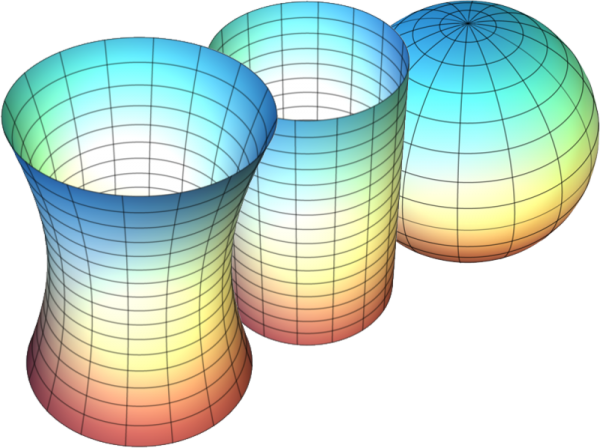
That depends on how speculative you're willing to get. On the one hand, the structure of space does have an overall shape on the largest scales, dependent on its curvature. If it's positively curved, it's shaped like a sphere, and will close in on itself. If it's completely flat, it could still be shaped like a torus, or a cylinder that loops around and reconnects with itself, like a donut. Or if it's negatively curved, it could be shaped like a saddle on small scales, but even these could close in on themselves in a complicated way.
In other words, regardless of the Universe's curvature, it could be either finite or infinite. And if it is finite, you'd be tempted to ask about the center. After all, if you imagine spacetime is a sphere, you'd say that the center of the sphere is the center. If spacetime is a donut, you'd say the center of the hole is the center.
But there's a problem with your reasoning, tempting though it may be.
You are thinking in three dimensions. And who can blame you, really? The problem is, all of these surfaces -- the surface of a sphere; the surface of a donut; the surface of a saddle -- are all two dimensional. And you are finding the center by going into the third dimension.
But space is three dimensional. Rather than the Universe expanding like the surface a rubber sheet (or balloon) getting stretched, it's expanding like a loaf of baking bread (in a zero-gravity oven), expanding in all three dimensions. When you're thinking of a sphere, a donut, or a saddle, you're thinking of two-dimensional objects, taking one dimension of space away. I can't blame you; visualizing an extra dimension is pretty hard! If the Universe actually turns out to be finite, and actually has a center, that center would exist in higher dimensional space!
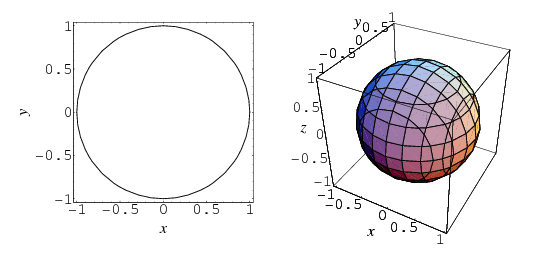 Image credit: Margherita Barile of http://mathworld.wolfram.com/.
Image credit: Margherita Barile of http://mathworld.wolfram.com/.
The surface-of-the-circle on the left is a one-dimensional line. It has a center in two dimensions, but if all you can do is perceive and walk along the circumference of the circle, asking "where is its center?" is a question that doesn't make sense.
The surface-of-the-sphere on the right is a two-dimensional plane. It has a center in three dimensions, but if all you can do is perceive and walk along the surface of the sphere, asking "where is its center?" is a question that doesn't make sense.
And then there's what we know as space. Our three-dimensional space.
 Image credit: Richard Powell of http://www.atlasoftheuniverse.com/.
Image credit: Richard Powell of http://www.atlasoftheuniverse.com/.
It's totally plausible that this is the surface of some higher-dimensional structure, and that structure actually has a center. But if it does, it's completely beyond our ability to observe it. Moreover, asking where is the center of our Universe is a question that doesn't make sense, the same way asking where is the center of a circle's circumference doesn't make sense.
And that is why the Universe doesn't have a center!
Have a question or suggestion for Ethan? Head over here and ask!




I am afraid I am about to make a fool of myself, but you often see those big bang graphics like the picture at the top of this link: http://www.universetoday.com/102783/kapow-keck-confirms-puzzling-elemen… where time is plotted as a separate dimension. Doesn't this mean that the center of the universe exists at t=0, where time is the radius of the metaphorical balloon of which the three spacial dimensions are the surface?
Or have I taken the metaphors inherent in these images too far?
In other words, the problem is the epistemological entanglement. Our languages, basically all of them including mathematics, except perhaps music, do not extend into the right kind of relationships with enough assurance in order to match any part of reality which might contain the center. The problem of center is that we intuit not only its existence but we intuit as well the abhorrence of a centerless universe. "No center" is just wrong. We know this. The deepest insight from the spiritual side of things: if center is nowhere, then the reverse must also be, and center is everywhere. But of course this is not science.
Ethan,
I'm well aware of the baloon analogy or your circle or sphere surface example. If that's how the universe works, I can say I understand why there's "no center of the universe" and have no problem with that.
However, even you put an "if" in all of that when you said: "if all you can do is perceive and walk along the surface...". This is what made me ask: "If we live in a 3D universe, and look at your spherical model, WHY would we only be able to walk along the surface and not within the sphere"?
Then I thought again and remembered our friend Einstein and his Relativity Theory which postulates that there is no "3D space" but a "4D spacetime" (in words better than mine).
I think when one considers that "detail", in addition to the analogies above, it becomes clear why we can perceive to live in 3D but still be unable to "leave the surface".
So, my advice to MandoZink and anyone wondering about the center is to read Einstein, starting with the special Relativity, and then the general Relativity. It is by far NOT as complicated as many journalists have made the general public believe - on the contrary. I recommend to read it as a story and not as a scientific work to anyone questioning if he or she is was up to the task of understanding it.
Ethan: I think your answer is wrong. Yes, it's pretty much the standard cosmologist's answer. What you'd call the consensus view.
But I still think it's wrong.
Sorry.
Center of the universe is where the bing bang started, exploded i think. No explosion goes only one way it goes every direction and i think universe has spherical geometry.
If I understand correctly, then, there is still a possibility that spacetime is flat--not just within the 1% tolerance we can measure so far, but truly flat. If that were the case, do cosmologists believe the universe could still have finite size (as they believe in the case of a positively curved, 3-spherical universe)? Because if the universe is flat and bounded, then that would imply there *is* a centre (and a periphery or edge), wouldn't it?
Given that necessary conclusion (if I've understood correctly), does this cause cosmologists to discount the possibility that the curvature of space is precisely zero, and to believe that when we can measure with enough precision, we will be able to determine the magnitude of a positive or negative curvature?
@5 Monty
if the space is totally flat then it's by default infinite. I say "default" because there is no theory or anything that would postulate or explain how spacetime just "ends" or stops. Just as in geometry and math, constructing elements are infinite... plane, line etc.. So if your building blocks are infinite, then you get infinite result.
For what you say to work, you will need a mathematical model in which planes don't extend to infinity
Sinisa - I hear you. Wouldn't this mean quite a radical departure from other beliefs, though, if space was flat and therefore infinite in extent: for one thing, if the universe was created in a big bang and spacetime was of finite extent then, a finite amount of time ago, how could its extent now be infinite?
Since there's probably no answer to that question, does it mean that in the case of a truly flat universe, flat empty spacetime was there before the big bang instead? I understand and have always accepted the usual view that spacetime was created at the big bang and any centre of expansion could only be reached by travelling through a dimension perpendicular to our 3 spatial dimensions, analogous to the 2-sphere expanding in 3-dimensional space. But if the universe really is flat, and therefore unbounded, what was it that had finite extent at the moment of the big bang?
To me, I can't see how the universe being flat (or indeed negatively curved) is compatible with a big bang where spacetime is created with only finite extent.
Ethan: It seems to me that you and MandoZink are speaking two different languages. When you speak of the entire Universe, I gather that you are speaking of all energy and matter and the sum of all space (including all dimensions) which is home to that energy and matter. But I believe Mando is speaking only of the matter and energy which originated from what he perceives to be the singularity which resulted in the Big Bang. I believe his question actually is whether there would be a discernible point on one of the surfaces you describe, which represents the point of the Big Bang and from which all matter and energy are expanding. I believe your response, briefly, would be that the Big Bang created the surface on which we mere mortals perceive the energy and matter to exist, and also created all of the dimensions, and it may be that the dimensions which are expanding. But the matter and energy are essentially evenly distributed on the surface we perceive. Correct?
That's helpful, Ethan, thanks. But when I conceive of the expansion of the universe I see it as an explosion, leading to an expanding football, but I see the outer layer, where the matter is, as having some depth, due to particles colliding, and probably the middle being misty. So even on the surface of the football we could see some way in the dimension towards the centre. How am I seeing this wrong?
Ethan:
I suspect the source of exasperation I felt reading this explanation may lie in the semantics of the question I asked. I also want to make it plain that I am NOT asking about the center of the "big bang", or any necessarily definable expansion point, other than a simple determination of instantaneous volume.
I have always comprehended the analogy of a rising, expanding loaf of bread to the expansion of the universe. But in that particular analogy I can also picture an instantaneous snapshot of that loaf's volume at a given moment. That 3D volume would have a central point. Even if the loaf was rising in some uneven, curved manner, and that point continuously varied, a 3D snapshot of it's instantaneous volume would be comprehensible geometry containing such a point at that moment.
So. I suspect the problem in my question may lie in the difference between casually using the term "universe" versus specifying "the volume of space representing the universe's current three dimensional limits of expansion at this moment". Your working definition of "universe" may include other dimensions of space/time/beyond/etc, which I can acknowledge, but I am only considering the 3D volume I might see if I could freeze time and survey the limits that space occupies at that instant.
Does that make sense?
I do see the element of time as a facet of the universe. I accept the fact that the universe likely extends into dimensions incomprehensible to current understanding. I believe I also understand the implications of the curvature of space. I can even visualize other universes whose arrow-of-time/entropy may be moving in vectors that are not parallel to ours!
What I cannot fathom is why a momentary three dimensional picture cannot be isolated from the expansion, unless somehow my use of the term "universe" is skewing the question.
Supplemental question: If the universe was only the size of a grapefruit (as has been described by physicists) about a trillionth of a second after the initial "expansion-event", was there no center to that either?
from the "... the size of the unobservable Universe is somewhere on the order of at least 150 times bigger than the part we can observe." link above:
What has changed in the last 15 months to alter estimates of either the overall size or the observable fraction of the universe by two orders of magnitude?
"... but I am only considering the 3D volume I might see if I could freeze time and survey the limits that space occupies at that instant."
I do want to clarify that I understand our universe does not "occupy" space. It defines the space that exists.
@8 Monty
" if the universe was created in a big bang and spacetime was of finite extent then, a finite amount of time ago, how could its extent now be infinite?
- spacetime could have been infinite before big bang. Before big bang there was inflation, and before that was something.. all of this is already in spacetime. Forget singularity and all that "from single point" crap. THAT IS NOT WHAT BIG BANG IS, and that is not how universe came to be.
"flat empty spacetime was there before the big bang instead? I understand and have always accepted the usual view that spacetime was created at the big bang ..."
- yes.. we were all thought wrong... or rather.. it was before inflation cosmology. The view of BB which you have (and as was/is thought in school) is riddled with problems. Physicists know this.. but it takes a bit to explain fully... so most just skip... Ethan covered much of it in posts, so search through the blog.
Basically.. you have spacetime filled with energy (unified field, inflation field, DE... name matters not), spacetime expands exponentialy (inflation).. that same field undergoes a huge potential drop and from that energy of that field is created all the matter. That creation of matter is called Big Bang. And it didn't happen in single point and then spread... It happened IN EVERY SINGLE POINT of allready inflated spacetime... in other words, it happened everywhere at once (or close to "at once").
A different way to look at infinity of spacetime doesn't have anything to do with BB. Instead... the metric of spacetime expands according to relativity. And given enough space separation.. it is expanding faster than the speed of light. Yup, can do that. However.. for everything "in" spacetime, speed of light is the limit. So, in principal, it goes on to infinity from point of view of everything "inside" the light cone.
@MendoZink
It seems to me there is only one way that a shape - be it 1 dimensional, 2-dimensional, 3-dimensional, etc. - can be such that the concept of a center does not apply to it.
A closed loop is a 1-dimensional form that has no end points (no bounding points), yet it is finite in length. And the concept of a middle point does not apply.
The surface of a doughnut is a 2-dimensional form that has no bounding edges, yet it has a finite area. No center.
It seems to me the Universe would have to be a 3-dimensional analogon of to make the concept of a center be not applicable.
(This is the line of reasoning that gives rise to speculations about a 'doughnut Universe', or a 'torus Universe'.)
(This must still be thought of as a very loose analogy. In the 1D and 2D case the visualizations are in a 3D space, so there is "room to spare". The loop is curved in an extra spatial dimension, so is the torus surface. It shouldn't be automatically assumed that with such a loop-back-on-itself Universe a yet higher dimension must be involved)
The torus surface can be thought of as geometrically flat in the following sense: you can lay out a grid on the surface and in _all_ local areas the grid lines will intersect each other at right angles. (As opposed to a sphere, where the lines of a grid will always intersect somewhere.)
@12 Butler:
Re-read the original link closer-- The "150 times" refers to the minimum radius of any potential curvature of the universe. But the 0.0001% refers to a volume, if I read that right. That can explain the orders of magnitude. But keep in mind, those are not estimates of the size, those are minimum constraints on the size. Constraint calculations do not have to agree (or even be remotely similar) in order to be valid!
@11 MandoZink:
Regarding "a simple determination of instantaneous volume", I do not even begin know how one would approach that determination. I think that your intuitive approach is actually asking a question that is far more tricky than it seems.
On Newtonian scales, taking a 3-D snapshot of a given space is probably straightforward, at least theoretically. You can define an instantaneous volume, including its shape, its borders, and calculate the geometric center. Just like you do with your drafting work.
But on the scale of the entire universe, one must think relativistically, not classically. How do you intend to define the region you want to find the center of?
For starters, there's a problem with the "instantaneous" requirement of your definition. Taking an "instantaneous" snapshot really means referencing multiple points simultaneously. On the universal scale, simultaneity is relative to your reference frame. So it is not clear to me that an "instantaneous" snapshot of the whole universe can even be defined.
You can't take an instantaneous snapshot of the entire 3-D universe, in any meaningful way. But it's what our 3-D-oriented brains desperately try to do.
Lets say you solved the simultaneity/relativity problem. What is next... do you measure the volume beyond the observable universe? By definition, it is unobservable. We don't know how big it is, or what shape it is. And size and shape, aren't they the key ingredients for calculating the center?
In the simplest case scenario that I can fathom, spacetime is closed.... And, like the center of a closed 2-D surface exists only in the 3rd dimension, the center of a 4-D closed universe would exist somewhere in a 5th dimension.
What I can't escape from, is concluding that the very concept of "center" as you propose, simply does not make sense on a universal scale.
PS @11 MandoZink:
"If the universe was only the size of a grapefruit (as has been described by physicists) about a trillionth of a second after the initial “expansion-event”, was there no center to that either?"
I found the talkorigins FAQ covering the Big Bang Theory to have a helpful explanation to this, which is good reading. The "size of a grapefruit" analogy does not refer to the size of the entire universe, or even a grapefruit-sized lump within the early universe. It apparently refers to the diameter within which the contents of today's observable universe would have to be compressed, to correspond to the earliest moments after the big bang.
I think it's nothing more than an analogy, offered to help lay people such as ourselves get a sense for how hot and dense the universe was back then-- i.e. take everything we can possibly see, and squeeze it down to the size of a grapefruit. It's that hot and dense.
That grapefruit did not have a center, any more than our observable universe today has a center, other than the observer himself.
Am I interpreting that correctly?
In my remark about laying out a grid on a sphere I messed up a little, but you get the point. Lines that start parallel will always intersect somewhere.
(And it's MandoZink; my apologies for writing 'MendoZink'.)
Mac @ # 16 - Thanks for ... well, not exactly clearing that up, but at least pointing out my (first) mistake!
@MandoZink #11: It sounds like the question you're asking is _not_ "was there a central point of origin to the Big Bang" (you say you understand that there was not), but rather, "where is the central point of the Universe we see today."
The answer to that question is trivial, and uninformative. We are precisely the central point to our own observable Universe. We can see exactly the same distance (with sufficiently good instruments) in every direction, basically a radius of some 46 billion light years. Therefore, we observe (in principle) a spherical volume surrounding us.
One of the points Ethan is trying to make is that our location isn't special. Observers on a planet located in UDFj-39546284 (the most distant galaxy currently known, at z ~ 11.9) would _also_ observe a spherical volume with a radius of 46 billion light years. That volume overlaps with ours.
Given the consensus cosmology including flatness and inflation, the volume of whatever it is that we are a part of is at least 150 times larger than what we can observe. We may or may not be in any particular "central" position in that larger space.
@Sinisa #7: You wrote, "If the space is totally flat then it’s by default infinite." I wrote roughly the same thing in a comment on this blog several weeks ago, and was very nicely corrected.
My ignorance of three-dimensional topological algebra tripped me up (and no, I still can't _picture_ the correct answer, but I accept it :-). It turns out that a torus is a mathematically _flat_ geometry. So it is possible (we don't have any observational evidence for it) that our universe is both flat and finite in extent.
I am not at all competent to explain why that is true (I'm an experimental particle physicist, not a mathematician), but I trust the mathematical experts I've asked about this.
@22 Michael
Thank you for pointing that out. Didn't know that before. Led me to check "flat torus", and admittedly not sure I fully understand it. But what I think I understand is that there is a difference between bending and stretching. And it only works in 4d space mathematically (according to wiki).. so, like yourself, I would have to agree without fully understanding. But for torus, we know there are mathematical transformations that make a plane become a torus.
But once you already have a torus, you can clearly observe that it is finite. What I tried to answer is that, if it's "truly" flat plane in 2d space/or 3d space. A plane.. without any transformation, by mathematical definition goes to infinity. At least in math at my modest level :)
Relativity doesn’t tell us that space is curved by the presence of matter and energy. It isn’t space that’s curved, it’s spacetime. See Baez and note this: ”not the curvature of space, but of spacetime. The distinction is crucial”. In the space where a gravitational field is, space isn’t curved, it’s inhomogeneous. See Einstein’s Leyden Address for that. Note ”empty space in its physical relation is neither homogeneous nor isotropic”. Also see this abstract. Then look at the FLRW metric which ”starts with the assumption of homogeneity and isotropy of space”. That’s fine. But it means there’s no overall gravitational field and no overall curvature. None. So the ‘flat’ universe was always going to be correct. It’s a non-sequitur to claim that a flat universe must be infinite. And we have no evidence whatsoever of any magical higher dimensions or mystic toruses. But we do know the universe is expanding, and we ought to know that an infinite universe cannot expand because the energy-pressure would be counterbalanced at every location. So you’re left with a finite universe that as far as we can tell is spherical. A finite universe with an edge. And a centre.
There is no such thing as a meaningful "The Observable Universe". Its is impossible to make any logical conclusion out of the concept "The Observable Universe", therefore the term has no meaning. If you pretend to do so, you make a fallacy.
It is totally wrong to say something like "That’s our observable Universe, as visible from our location in space. The part that we can see is — to an excellent approximation — spherical, and about 46 billion light-years in radius, centered on us."
"46 billion light-years" Is clearly used as a distance. And it is a calculated distance, taking in account the expansion since the moment that the light we can see started traveling to us. That is a calculation based on a a Cartesian coordinate system with as origin the starting point of a photon, far away. Thus for each direction we look a different coordinate system. And that makes our position fuzzy. Even unknown. We can't be the center of that, because there can not be an exact position calculated.
Would those "46 billion light-years" be a measured distance then we have to take in account the nature of light not traveling at a infinite speed. Therefore measuring distance is really measuring time. Meaning, although the origin of the coordinate system is known (our position), there is no possible measurable position far away, because each point is history. That makes the "radius" fuzzy, and us center of a fuzzy meaningless concept.
So. Answering the question "So let’s get to it: what’s the deal with the geometry of the Universe, and whether (or not) there’s a center?" always makes the idea of a "The Observable Universe" obsolute.
If the big bang theory is true (which is don't doubt), then the center of the universe is all around us. Because in any direction we look and measure (due the speed of light) we look back in time, closer to the Big Bang. Thus closer to the center of the universe as we should see and be able to measure it. In all directions means that measuring can not render a position, not one point in any coordinate system. While the question asks for a position.
Coming back to the fallacy. Allow me to illustrate this. Since looking back in distance is the same as looking back in time, al we see is a projection. Like looking at an old movie. As if you can sit in your living room explaining the "The Observable Universe". Pointing around you to the walls and say: this is the "The Observable Universe". Pointing to the TV and say: "I can see New York". Superman from 1978 is on TV. You can indeed see the twin towers.
I always thought the circle and sphere analogies were pretty clear; however many dimensions in your space (let's call it N), the "center" isn't in your space, it resides N+1 dimensional space. So, the "center" of a 1-d circular line isn't on the line, it resides in 2-D space. The center of a 2-D spherical surface isn't on the surface, it resides in 3-D space. The center of our 3-D volume isn't in the volume, it resides in 4-D space.
The geometry questions are much more interesting, IMO, because while the "not in our space" answer is possible, it isn't necessarily true - it depends on geometry. Sure, a circle has no 1-D center. But a straight line of finite extent does. The surface of a sphere doesn't have a 2-D center, but a finite, flat plane does. Sticking to surfaces, a torus has no such center, but a saddle shape does.
Now, maybe the math of 3-D volumes is not directly analogous to 2D surfaces and so you get different answers. But from the 2D cases, reasoning from analogy would lead me to believe that there are some 3-D geometries which have a center (in the 3-D space) and others that don't, and that maybe the characteristics of open vs. closed, infinite vs. finite matter when answering that question. Thus, finding that our universe is flat may give us some insight into whether there is a center in our 3-D space or not. Likewise, one could hypothesize flat-finite and flat-infinite and see if that makes a difference. Unfortunately, I"m not enough of a mathematician to say what that insight is, or even if we really get one.
@Eric
"some insight into whether there is a center in our 3-D space or not"
if relativity is correct, then it matters not. We are, and always will be the center of our own bubble universe (observable universe, not now but ever). Everything beyond it will always be outside our causal reach. Unless metric expansion switches sign for some reason :D
My personal belief is the curvature will be as near to 0 as we can measure. (just a hunch)... nothing set in stone.
But ramifications of relativity are that it's physically impossible to get anything outside of the "bubble" dictated by the speed of light.
Space-time is outside our sensual experience and so not amenable to three-dimentional understanding of center.
Ethan,
Thank you very much for attempting to answer the question that I appeared to ask. The conceptual understanding I was seeking has been seriously misinterpreted by a lot of people who responded here. Apparently I did not convey what I really wanted to find out.
The subject of my question involves the space that the universe has expanded to, including that which we longer can see - that space having been created by the expansion, with my full understanding that it's boundaries define the space that exists.
I wanted to understand if space is a volume comprehensible in the same x/y/z manner that we understand 3D geometry. My question as to a center was arbitrarily derived from the simple understanding that in the common vernacular of geometric calculation, a volume has determinable midpoint.
To many of you who responded, I did NOT think there was a "designated center" or "center of expansion". Nor did I think we could actually take a snapshot of the expansion boundary at any instant. That was simply hypothetical.
All I wanted was an explanation to help me understand the exceptional nature of the properties of an x/y/z volume that would deny it having a centric determination. That understanding appears to be second nature to astrophysicists. My comprehension of this space needs to expand beyond more comfortable geometry.
Obviously there is an astounding nature to the volume we occupy. If anyone knows of any competent and inspired video animations which expound on the deviations and eccentricities in the geometry of the universe, I would greatly appreciate the posted links.
Once again, thanks.
Ron Seadler
@ MandoZink
I carefully read your last post and would ask if you can elaborate on some of the things you ask. Because IMO it doesn't make sense from physics standpoint.
"The subject of my question involves the space that the universe has expanded to"
- if treated concerning the whole universe then it makes no sense.. the universe didn't expand into any space. Spacetime is part of the whole universe. If you are asking about the space that the matter filling our observable universe filled... it's spacetime.. same as the one you have in your room. Are you asking about the properties of it? before BB properties.. that's the domain of inflation study.
" that space having been created by the expansion"
again, this doesn't work.. expansion of universe doesn't create any new space.
"with my full understanding that it’s boundaries define the space that exists."
what do you mean by boundaries?? are you talking about our observable universe or whole? as it is the question makes no sense, there are no boundaries is the simple answer, yet i have an impression this is not what you ask.
"I wanted to understand if space is a volume comprehensible in the same x/y/z manner that we understand 3D geometry."
simple answer.. yes and no. yes.. you can "aproximate" a lot of things or even simplyfy. like our observable universe is a sphere with earth as center. but you forget that it's not space. it's spacetime.. it's 3D+1time.. and that time is very real.. that 4D thing stretches, contracts, flows.. it's dynamic and essentially tied to every thing inside it. Your own mass/energy changes it constantly, and your mass/energy moves accordingly.
You ask about volume, yet I don't understand what you mean.. which goes back to boundaries.. what boundaries?
That's what the discussion was about.. in flat spacetime there are no boundaries.. hence no relevance for volume.
If you want to learn about geometry of spacetime. Relativity is your only way. How lightcones, histories work and how spacetime behaves. it's all geometry.
@Sinisa Lazarek (and others)
This is a bit frustrating.
"the universe didn’t expand into any space. Spacetime is part of the whole universe"
I have understood that for years. That is NOT what I am trying to get a better understanding of. I will explain several paragraphs from now.
First, you need to know what I DO know. I have understood light cones since the early 70's, and totally understand the concept. I have a complete grasp of redshift and the superluminal expansion of the universe. Recently I finished an academic paper describing common misconceptions of cosmological horizons caused by the special relativistic Doppler interpretation of redshifts. Not a problem.
I have always read nearly every informative article on cosmology that ever caught my attention. I immersed myself heavily in Sean Carroll's descriptions of entropy and the arrow-of-time, even writing and receiving responses from him. I have watched countless lectures on astronomy and cosmology. For over 20 years I have caught nearly Science Friday on NPR and watched nearly every documentary on PBS.
As for mentions of relativity, I often have a habit of doing calculations with SR and GR just to see how the results bear out the effects that astronomy and physics describe. I understand, in a very-real-to-me sense, that space-time is the universe we exist in.
To shorten this elucidation, the informational input I have fed myself for 40 years is immense. The concepts I have a grasp of are extensive.
So here is a longer and (hopefully) better-framed question:
----------------------------------------------------------
The evolution of this universe, and the speculations as to whether were are part of a series of multiverses, always describe the inflation-event and it's result as a "bubble", or as one of many "bubbles" in some multiverse scenarios. Each "bubble" creates it's own space-time. What is outside of that "bubble" is NOT space-time. Basically, an observable "there" does not even exist on the outside.
In their analyses of the universe immediately following the "big bang" event, physicists often attempt to characterize it's size after mere trillionths of a second. At one terasecond point it's described as being "the size of a grapefruit".
These portrayals infer a containment. The descriptive language being used here is no less than the lexicons of geometry that imply both volume and magnitude.
Is there?
With this in mind I now ask (hypothetically of course), suppose you could stop time at a given instant. Then you proceed to travel out, in the frozen, "not-now-expanding" space, in one direction. What would you eventually find? Where would you go? What would you eventually reach?
The center that I said geometry would suggest is not really the issue here. But as implied by their language ("bubble" and "size of a grapefruit"), is there not a volume being contained on some level?
----------------------------------------------------------
I do not fear a conceptual re-adjustment. A suitable analogy that generates the epiphany I seek would do just fine.
This was mentioned earlier. What is apparently being referred to as "the size of a grapefruit" is the volume (at that time) of what is now the entire observable universe -- it's a way of characterizing the density then, relative to the density now, not a way of telling how "big" space was or is, or of saying anything about whether it has a boundary. It's very reasonable to assume the universe as a whole keeps going beyond the observable part, no matter what time we're talking about. So you'd want to ask "how much farther does it keep going past the grapefruit-sized chunk?" No one knows, as far as I'm aware.
There's no meaningful way to talk about a "center" of an infinite spacetime, so the question is poorly-defined if it's assumed that it being infinite is impossible. Given the "flatness" of spacetime described above, based on my very amateur understanding of the physics it seems like it probably is infinite, so the answer to your question is that there is no center, because an infinite volume has no definable boundaries, with which you would have to make such a measurement (not even as a "hypothetical" measurement that we merely couldn't make in practice).
On the other hand, if it's finite, then the parts that you might have assumed were "beyond" the universe might have actually been in it without you realizing that. In other words, there may not be anywhere else to go, which doesn't imply there is a center of everything. People have already discussed "flat" finite geometries, like a torus for example (of course it would be a higher-dimensional version to make room for 3-space plus 1-time plus any more actual physical dimensions if those exist), in which it's entirely consistent to say that it has a finite volume and no center, because it's analogous to the two-dimensional surface of a "regular" torus/doughnut. Do not focus on the third dimension when looking at a doughnut, because that does not correspond to anything real here -- just the surface, which goes around and around in any direction, meaning the surface doesn't have a boundary and thus it has no center. Moreover, if spacetime's not flat but curved, in any number of bizarre shapes, it would not need a boundary. Those are all possibilities, none of which suggests that space must just "stop" somehow.
The "bubble universes" you mention (supposing there is a multiverse) suffer the same as all analogies: they are taken too literally. Imagine the surface of the bubble, and you once again get something like the spherical case or the toroidal case or any number of other cases. Or if you mean to be referring to some extra physical dimensions in which our bubble and others exist (which aren't just handy abstractions for doing math that don't happen to correspond to anything real), then the question about a center still may not make any sense, because those extra dimensions might be infinite or curved or any of the options already discussed above without them. So those wouldn't change anything, because their mere existence certainly wouldn't imply they must have a center. Because the issue here is really one of an entire dimension (more than one), not simply the extent or volume of some particular shape in a dimension. Not to mention that there's no telling whether we'd ever be able to answer that particular question with any certainty, because there may not be any way for us (or anyone or anything) to do any measuring in those extra dimensions.
@Mando
Thanks for giving some background on what you know. Is clearer now.
I think I understand your question now, or where the problem is.
"In their analyses of the universe immediately following the “big bang” event, physicists often attempt to characterize it’s size after mere trillionths of a second. At one terasecond point it’s described as being “the size of a grapefruit”."
It's not size. I think this is what confused you. It's scale factor. And it's not just a choice of fancy words, it's conceptually different.
We don't know the size of our Universe. Don't know it now, don't know it then. We know the size of our observable part now, but we also know it's minute in comparison with the whole Universe. When I say Universe I mean our bubble Universe of Multiverse. Not our observable bubble.
So grapefruit part is only a bad analogy of our observable part 13.8 billion years ago. But that's not the Universe. It's only a fragment of the Universe. Noone knows how long inflation lasted, no one knows how big or small was it before inflation, thus noone knows how big it is now. That's why anything doing with size is unanswerable. Scale factor is different, it's a number of the increase of that unknown. i.e. it was some size then.. now it's 3 times as big. thus scale factor of 3. But I still don't know the size then or now.
"These portrayals infer a containment."
Yes, and that's why they are misleading. There is no containment.
"With this in mind I now ask (hypothetically of course), suppose you could stop time at a given instant. Then you proceed to travel out, in the frozen, “not-now-expanding” space, in one direction. What would you eventually find? Where would you go? What would you eventually reach?"
If Universe is homogeneous and isotropic, then you wouldn't find anything different then the place you set out from. If you remember the grapefruit being our observable part only, and if you could at instant freeze time and travel outside it, you would still find the same things as in your grapefruit. You wouldn't reach anything special just same matter and energy that you had in the place where you started from.
There is no physical boundary of any kind either in our observable bubble, or in anything dealing with early Universe in terms of spacetime.
The only boundaries worth exploring are the ones of Bubble Universe boundaries within Multiverse (if it exists). But since we don't know anything about "outside" and we don't know exactly what drove inflation, no one can give a scientific answer to that.
Hope this helps.
MandoZink - I like your last reformulation of the question. The original understanding I held for a long time about your original question is probably one you have heard before: just like the 2D ants on an expanding balloon, the center of the area they are confined to does not exist on that surface itself; rather they would have to travel in a 3rd dimension inaccessible to them. For real-world ants of course they could reach this center of the balloon (e.g. by tunnelling through its surface then dangling from a string :-), but in the thought experiment they are truly 2D creatures and constrained (by what?) to remain on the untearable surface of the balloon. So, on to us: we can move around this 3D volume at will, but--on a much larger scale than we will ever have time to encounter--this 3D volume wraps around on itself in some unattainable 4th spatial dimension, and so there is no center to our volume within that volume; our volume (a hypersurface, really) is at a remove from the point in the hypervolume in which it resides. If we were to freeze the universe, and grant ourselves the ability to travel unlimitedly fast in any spatial direction, we still could not be expected to be shown the center of the volume we exist in, because that volume "wraps around" on itself like the surface of a higher-dimensional sphere. In order to visit the higher-dimensional center we would have to be transported through a 4th spatial dimension that is apparently inaccessible to us--maybe the question should be why travel in this dimension should be inaccessible, if it is a large enough dimension that the entire universe can be wrapped into it.
Now, I don't see how that whole story can be held as necessarily true any more, if we don't know for a fact that the curvature of the universe is positive. For surely that is required for the analogy to hold. The ants can't reach the "true" center of their balloon because the balloon curves positively and creates an unbounded yet finite surface--they encounter no edge as they travel around it.
Your last reformulation is interesting too. I have wondered, like you, about the medium in which bubbles of inflationary space time are supposed to be expanding. Do the bubbles create new space as they expand, or do they "eat away from within" the medium in which they nucleate? If the latter, you would expect individual universe bubbles to occasionally intersect with each other as they expand, like holes in a swiss cheese that combine to form larger holes. If *that* can happen, then I wonder what happens at the boundary, since the individual bubbles in this multiversal swiss cheese are held to have different laws of physics. I asked this very question in a reddit thread not long ago--the "askscience" subreddit is sometimes quite good--and got some answers here: http://www.reddit.com/r/askscience/comments/1han74/expanding_bubbles_in…
@Mando: IMHO you've been getting some non-answers here. Stick to your guns. Pursue your point. Do not be fobbed off with bubbles and multiverses. Do not settle for turtles all the way down.
nice post, but wrong.
if there's a bright center to the universe, it's the point that is farthest from Tatooine.
:)
I'm getting a bit fed up with people giving Mando non-answers like "the multiverse". Relativity tells you space is a something rather than nothing. Electromagnetism tells you that waves run through it. Cosmology tells you it started small and is expanding. Classical physics tells you that an infinite thing cannot expand. But there is nothing that tells you that space is some higher-dimensional mystic doughnut. So what are you left with? The very thing Mando is asking about. Mando: here's what I think:
http://bogpaper.com/2013/09/22/science-sundays-with-john-duffield-edge-…
The balloon analogy is great for explaining how you can have a finite, yet boundaryless and centerless surface, even if it is expanded and everything looks to be moving away from you.
It fails as soon as you ask "What is the balloon expanding into?" and picture it filling with air, and displacing the air in the rest of the room.
While you can visualise the surface embedded in a higher-dimensional space, that doesn't necessarily mean anything. I can define a 2D torus -- a flat, finite surface where if you go in one direction you'll eventually wrap around to where you started -- without ever referring to a 3rd dimension.
Now that I think about it I've played a number of video games which model such a surface, mostly quite old.
We can similarly model inflation or the present-day expansion of space as space itself expanding, without a higher dimension. The space in which inflation occurred became bigger. It doesn't have to displace anything to do this, it just changes geometry.
That doesn't mean there aren't additional dimensions. It just means that they aren't needed to understand the concepts today. You'd want to work out additional implications for these extra dimensions; "inflation now makes sense" isn't one of them. A better inflationary model might be.
Good answer on the scale of the universe, Sinisa.
"Classical physics tells you that an infinite thing cannot expand."
No it doesn't.
"But there is nothing that tells you that space is some higher-dimensional mystic doughnut."
Yes there is: the math of General Relativity, which tells you what the possible geometries of space-time are and how to distinguish based on measurements. The geometries that are consistent with current measurements are flat-and-infinite, and flat-or-very-nearly-so-and-closed-finite.
Note that this doesn't mean it's embedded in a higher dimensional space.
You can't take the surface-analogy-level implications of GR while ditching the deeper mathematical meaning.
@Mando:
*With this in mind I now ask (hypothetically of course), suppose you could stop time at a given instant. Then you proceed to travel out, in the frozen, “not-now-expanding” space, in one direction. What would you eventually find? Where would you go? What would you eventually reach?*
To answer your questions:
If space is "closed" as Nathan is saying, you would come back where you started. In fact, if you and your friend simultaneously set off in opposite directions, then eventually you'd see your friend approaching you from the front.
(This is analogous to 2 people on the equator of the Earth, one setting off East, and the other heading West. Eventually they approach each other again).
On the other hand, if the universe is "open", you just keep going on forever and you never see your friend again.
@Mando:
“In their analyses of the universe immediately following the “big bang” event, physicists often attempt to characterize it’s size after mere trillionths of a second. At one terasecond point it’s described as being “the size of a grapefruit”.”
They are referring to the size of what we is NOW the entire *observable* universe at one terasecond after big bang.
Now if the *entire* universe is closed, it would be much smaller than its current size one terasecond after the big bang, but it could still be a lot larger than the grapefruit which becomes our observable universe.
The way I think about it is - the entire universe is a globe and the observable universe represents a patch on that globe. So, as you approach the Big Bang, both the globe and the patch shrink proportionately.
If the entire universe is infinite, then however close you get to the big bang, it remains infinite. But the observable universe keeps shrinking in size.
Cosmonut: An even more succinct explanation. Cheers.
The universe is probably infinite in extent. There's no center to infinity.
(Apologies if somebody already said this...)
"But what about the Big Bang" I hear someone asking.
The Big Bang did not happen at one point in space. It happened at every point in space.
I believe the main issue people have with understanding these concepts is not understanding a few things...They don't understand what these words mean. Infinite by all definitions CAN NOT EXIST in a world that we exist. An infinite universe can not expand and an infinite universe can not start. In other words and infinite universe must have always been. There is a concept called potential infinity. The universe we can observe appears to be expanding at an accelerating rate or in other words - at an exponentially increasing rate - so it is potentially infinite. Therefore we should assume that the universe is an expanding sphere assuming that the big bang has any semblance of a explosion or release of high pressure - the path of least resistance will be towards lower presure (density) in all directions.
So here is my understanding of the observations.
Everything outside the universe is a piece of infinite 3d graph paper - it literally goes on forever it is truly infinite.
A simple 2d explaination would be. r = (t)+v^(e-g)
radius = time + initial velocity ^ rate of expansion - force of gravity.
In my mind i can see that this wouldn't produce a perfect sphere in all directions as the force of gravity would be different due to entropy within the system. I imagine if we could see the universe as a whole it would look like a giant some what spherical amoeba. Just my take...seems logical enough to me.
The point im trying to make here though is that in my understanding of the universe - which is potentially infinite and has flat space. There is most definitely a center. It can be found by finding any points inverse and diving by 2...It most definitely has an edge that can be found with the radius formula coming from any axis of the vertex. There is literally nothing outside of it.
"An infinite universe can not expand"
Actually, Hilbert shows that this isn't the case. An infinite universe can expand. It takes up a bigger infinity of space.
Infinity is REALLY REALLY weird.
"and an infinite universe can not start"
Well it couldn't be infinite and have a finite start and expand from one to the other.
This is just astonishing. For some reason, the people who try and explain these things seem to be so in love with the sound of their voice and find such satisfaction with confusing things..as if we are all just idiots.
Such are answers about a center and edge of the UV.
In a fraction of second the Universe was the size of a grapefruit. A grapefruit has a center and an edge and so did the universe. Subject closed.
Flat is only in relation to ecludian geometry. It has nothing to do with a center. The ballon analogy is also ONLY to demostrate the space between galaxies is expanding. A loaf of rasin bread is a better picture and it too has a center.
Because matter curves space, if you got to the boundary you would feel like u were going straight as you would essentially "orbit" the Uv. U would not see an edge...but just as the grapefruit sized UV must have a boundry..this UV does have one now. If space is expanding faster than light, photons could never reach this boundry to bend around it.
But scientists need to stop over explaining as they think they are dazzling us idiots. There is no such things as an actual infinite and an expanding infinite is even more incoherent. A loophole like set theory cant help in reality either
What we have here is a bunch of people just repeating what some guy they think is smarter than them said. So the next time you hear the UV has no center or edge as if someone just blew your mind...ask them how they known this, and ask them if the basketball sized universe is also devoid of geometry
Sorry, I didnt read that people did mention the grapefruit.
But saying thats a bad analogy is wrong. Look, I dont know why people insist on trying the confuse the subject as if some amorphous glob of interdimensional pseudo space that is beyond human comprehension was there.
There is no provable scientific evidence that states our universe is anything but 3 dimensions...yes the very 3 we all walk through everyday. That means if you were created through a fluctuation at the millisecond the UV was just a little bit bigger than you...you would be in its center.
Or if you could hold a tiny UV in your hands...extrapolate from there....
All Im saying is why this stubbornness persists is an ongoing problem among cosmologists. It occurs as they claim Time is an illusion ..a static block..and in the next breath they claim this motionless block is 13 billion years old. I think we would all rather hear things like...we just dont know, instead of an infinite series of recurring "we now know" proclamations
chuld the Center be mooving or not? chuld he be an apsolute location? if yes, in relation to what?