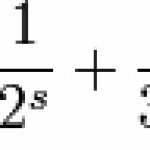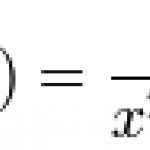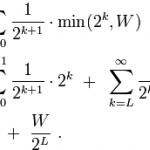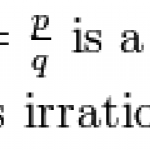Sunday Function
mspringer | August 1, 2011A reader asked me about the hyperbolic trig functions, sinh(x) and cosh(x). What are they for, and do they have an intuitive interpretation in physics?
That's a pretty good question. After all, most of the time you first meet the hyperbolic trig functions in intro calculus, where their rather odd definitions are presented and then used as test beds for blindly applying newly-learned differentiation rules. Ok, great. But what are they really?
To answer the question, we should start off with Euler's identity, which relates the exponential function with the regular trig functions. Proving this…
mspringer | March 14, 2011A while back I was driving in my car listening to the radio and was gobsmacked to hear a song (What's My Name? by Rihanna and Drake) in which the singer's rap involved accurately estimating a square root. Unfortunately it was in the context of a rather vulgar play on words ("the square root of sixty-nine is eight-something..."), and in fact the local station is now censoring everything after "square root". But still, mathematics on the pop charts! Who'd have guessed?
So today's function is the square root function, familiar to adults and school children alike:
As the kids are told by their…
mspringer | February 27, 2011Here is a picture of the earth, with latitude and longitude lines in ten-degree increments:
Despite the fact that each vaguely rectangular area formed by the intersection of those lines forms a 10 degree by 10 degree region, the actual square-mile area of each rectangle varies. The ones near the poles are smaller than the ones near the equator. It turns out that the area of a little square patch of land with sides given by some fixed interval of latitude and longitude will be proportional to cos(φ), where φ is the latitude. (NB: for those who're used to seeing sin(φ) in their spherical area…
mspringer | January 22, 2011In my free time during data acquisition runs and the like, I've been paging through Hardy and Wright's famous textbook An Introduction to the Theory of Numbers. It has something of a legendary reputation among pure math textbooks, and so far as I can tell it is entirely deserved.
One of the topics treated in the book is the representation of numbers in the decimal system. In some ways it's an elementary topic, but it also serves as a starting point for some genuinely deep mathematics. Today I'd like to noodle around with the connection between fractions and decimals. It's a bit of a stretch…
mspringer | January 17, 2011This Christmas I got a little handheld GPS, which I've been using mostly for geocaching. As the device acquires signals from the various satellites dutifully orbiting overhead, it displays your position coordinates and a figure indicating the estimated uncertainty. At the beginning of the acquisition or if the view of the sky is poor, it might be something like 50 feet. If you have a clear view of the sky and are receiving signals from many satellites, it might be as low as 11 or 12 feet.*
This figure is called the circular error probable. In essence, there is a 50% probability that your GPS-…
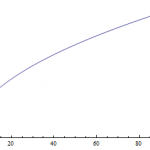
mspringer | November 21, 2010In pure mathematics there's not too many function studied more than the Riemann zeta function. For reasons of historical tradition, the generic variable name that's usually used is s instead of z. (The function is mostly interesting in terms of complex analysis, so x would be a bit unorthodox too.) It's defined in the following way:
On the real line, it looks like this:
Not terribly exciting, most of the interesting action happens for complex values of s. The reason that the action is interesting is that the zeta function is intimately connected to the prime numbers, despite there being no…
mspringer | November 7, 2010Most textbooks, especially ones not aimed at college math majors, give a definition of "function" that seems quite intuitive. They'll say something along the lines of: a function is a rule that takes an input x and turns it into an output f(x). Formally this isn't quite right - the essence of a function is in the set of ordered pairs {x, f(x)} and not in the specific rule that connects them. There doesn't even have to be such a rule.
But the idea of function as a machine is such a powerful and intuitive one that it tends to be used pretty universally until you have a good reason to abandon it…
mspringer | October 17, 2010Here's a straightforward function of two variables, x and y:
Its domain is all real x and y, with the single exception of x = y = 0, which would make the denominator 0. But we have experience with functions such as sin(x)/x, where we can find the limiting value as x approaches 0 and just make a fiat declaration that that limit isthe value of the function at the origin. Can we do it here?
Well, let's just tabulate the value of f(x,y) for different values of x close to 0 and see what happens:
f(0.1, 0.1) = 0.0990099
f(0.01, 0.01) = 0.009999
f(0.001, 0.001) = 0.000999999
This suggests that if…
mspringer | September 26, 2010Death and taxes. And dead is dead, but taxes come in a huge panoply of forms. There's property taxes, excise taxes, sin taxes and income taxes. There's gas taxes and sales taxes and VAT taxes (yeah, I know) and death taxes.
With my politics I'm not a huge fan of any of them, but they are what they are. And every once in a while they produce some interesting math. One of the more interesting taxes, mathematically speaking, is the capital gains tax. It works like this: you invest your money in stocks or bonds or some other investment vehicle. In an ideal world your investment grows in value and…
mspringer | August 29, 2010If you go to the bank and open a savings account, the banker might tell you about the virtues of compound interest. He may say something like "Even if you never deposit anything, the rate of change of the money in your account is proportional to the amount of money in your account. The more you earn, the faster you earn." Now the banker is less likely to use such explicitly mathematical language, but what he's telling you is actually a differential equation. A differential equation is an equation that relates a quantity to the rate of change of that quantity. The banker is relating your…
mspringer | August 22, 2010Here's an odd little bit of math for you this Sunday. It's defined in terms of recurrence. Recurrence happens when a function is defined in terms of itself. This happens more than you might think - one famous example is the Fibonacci sequence, which is informally defined by saying "To get the next term in the sequence, add the previous two terms together. The first two terms are 1 and 1." And so you can calculate that the sequence is {1, 1, 2, 3, 5, 8, 13, 21...} and so forth. That sequence turns out to show up in various odd places in math and science, and recursively defined sequences are…
mspringer | August 15, 2010So I spent two weeks in Wyoming, participated in a wedding in Louisiana, moved two apartments worth of stuff, visited Louisiana again to get a marriage license for myself (20 days left!), collected data for an experiment demonstrating a new result we're trying to get published quickly (hot topic, lots of competition), and so forth. Blogging is fun, but in terms of priority it has been taking a backseat.
For some reason, I feel the Busy Beaver function might be a good topic for this Sunday...
Ok, consider a Turing machine. I've embedded a video of a guy who's actually built one, but so you'll…
mspringer | July 11, 2010Again, apologies for the hideously scanty posting. Been in the lab doing some really interesting research which will with some luck get me in a really nice journal, as well as doing the various rounds of revision on the paper for some previous research. Also putting two talks together for a conference/school. That whole wedding planning ain't doing wonders for my spare time either. But hey, these are all good things so I'm not complaining.
I can at least write up a Sunday Function for y'all. This is one we've mentioned before, but haven't actually derived. I think it's high time we did. As…
mspringer | July 4, 2010Happy birthday to the United States! It's one of the younger countries on the planet and yet has still managed to have one of the oldest continuous systems of government. Not too shabby. Here's hoping our current wobbles get straightened out and our next few Independence Days occur under more pleasant conditions.
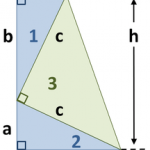
I'm not sure what function might fit very well in the context of this holiday, but I'll make sort of a stretch and do a function about the Pythagorean theorem. The Pythagorean theorem is a very ancient discovery with numerous different methods of proof. One of them was discovered by…
mspringer | June 13, 2010A while back I mentioned the St. Petersburg paradox. It's a hypothetical gambling scenario where you win money based on the outcome of a coin toss. If you get your first tails on the first throw, you get $1. If you get one head before your first tails, you get $2 dollars. If you get two heads before tails, you get $4. If three heads before tails, you get $8, and so on doubling each time.
How much should you be willing to pay to play this game? If you work out the mathematical expected value of the game, it turns out to be infinite. Play this game enough times and it doesn't matter how much it…
mspringer | June 6, 2010Back in 2003, I was a college freshman sitting in my first college math class - Honors Calculus I. On what was probably the second or third day of class, the professor gave us a surprise quiz. It was something like: "Give the formal statement of the principle of induction". It was my first graded assignment of my college career, and like most of the class I got a 0 on it.
Which was the professor's point - he had gone over it in great detail previously and was baptizing us by fire into the world of mathematical rigor. We didn't yet understand that mathematics both requires great attention to…
mspringer | May 23, 2010You're a member of the French Resistance in the height of WWII. You're part of a network of resistance members who have to work with other resistance members they've never met before. For instance, an agent from Paris might have to meet up with an agent in Normandy to work together on sabotage before the invasion. But resistance is not something the Nazis take lightly, and they've deployed double agents who attempt to infiltrate the resistance. The agent in Normandy needs some way to verify that this person from Paris is in fact a resistance member rather than an enemy double agent.
One…
mspringer | May 16, 2010Consider this not-so-difficult sum:
It consists of just a string of fractions up to whichever N you happen to choose. Add them up, and you certainly and unambiguously have a number. If you chose to stop at N = 10, you'd find that f(10) = 1627/2520, which is about 0.645635. If you chose to stop at N = 100, you'd find f(100) = 0.692647. If you've taken calculus in college, you can show without too much trouble that as you make N larger and larger, f(N) will close in on the value 0.6931471806..., which happens to be the natural logarithm of the number 2. As such you could say the sum of…
mspringer | May 2, 2010It's been a while since we've done a Sunday Function, so let's get back into the swing of things with a weird one. This is Thomae's function, and using Wikipedia's conveniently typeset definition:
If you're new to the concept of rational and irrational numbers, it's pretty simple. A number is rational if it can be written as a fraction p/q. Otherwise it's irrational. Numbers like pi or the square root of two fit this description. For this function we assume that the fraction p/q is reduced as far as possible, so if x = 1/3 we have p = 1 and q = 3. This is opposed to something like p =…
mspringer | April 4, 2010Happy Easter, everyone!
This Sunday Function is going to be short and sweet, since unfortunately I've got a lot to do before Monday. Let's get down to business!
Here's a function I've made up out of thin air. It's pretty arbitrary - in fact, it's discontinuous at x = -1/2 and not differentiable at x = 0:
Here is a huge pile of sine and cosine waves, with one bonus constant line which, if you'd like, you can think of as a cosine wave with infinite wavelength:
And here is what you get if you add all of those waves together and graph the result:
It looks quite a bit like the random crazy…