A Black Hole without a Singularity

Posted by Ethan on November 25, 2009
(60)
More »

All that matters, in the real world, is that something is both massive and compact enough so that, within a certain radius, light cannot escape from it. That is the astrophysical definition of a black hole. -me

We’ve been talking about black holes a lot recently, and with good reason. They’re fun to think about. These objects that collect matter, energy, light, and anything else that dares to cross its event horizon. It’s only natural to ask what might lie beneath that dark area that no light ever escapes from.

Image credit: mondolithic.com.

In 1916, everyone assumed that whatever happened inside a black hole, it must be powerful enough to simply destroy everything inside of it, and crush everything down to a singularity.

But this isn’t necessarily true, and I’m going to show you a simple example of how you can have a black hole, using only known physics, that doesn’t have a singularity at all.

Above is an artist’s rendition of a neutron star. A neutron star is an object that’s about the mass of our Sun, but with a radius of only around 5 kilometers. Well, if we could get that radius down to about 3 kilometers, no light would be able to get out.

That’s the definition of a black hole. A neutron star is already really, really close! Well, what are neutrons made out of?

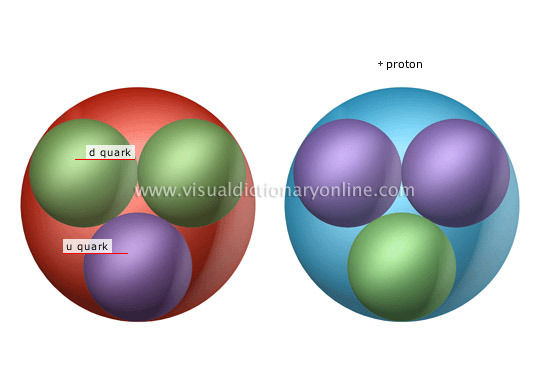
Quarks. Specifically, three of them: two down quarks and one up quark. Down and up are the two lightest quarks that we know of, and so the neutron has a total energy of about 1 GeV. But we know of six quarks, and we have many different combinations that could make a neutral particle just like a neutron.

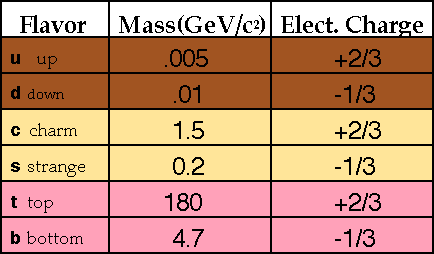
Let’s say, instead of two down quarks, we just replaced one of the down quarks with a bottom quark. Why do I pick this combination of “up-down-bottom”? Because we’ve discovered it, and it’s about six times as massive as a neutron. You make a star the mass of the Sun out of those, and do you know what happens?

Your density goes up, and your volume goes down. If you’re suddenly smaller than a neutron star, it only makes sense to ask “by how much?”

Well, if every particle is six times as massive, then you only need one-sixth the number of them, so your radius is ³√(6) times smaller than a neutron star. How big would this “bottom”-neutron star be? Only 2.75 kilometers in radius! In other words, it would be a black hole, and no light would ever get out!

And there’s no need to have a singularity, it would just be like a plain-old neutron star in every way, except it would be just a little denser than normal. And that’s just one of many simple possibilities! Have a great Thanksgiving, and I’ll see you all soon!

(60)
More »

Comments

  1. #1 sean hogge
    November 25, 2009

    And at that mass, the inward pull of the increased gravity wouldn’t overcome the degeneracy pressure? I guess that’s only a valid question if degeneracy pressure doesn’t depend on the mass of the particles involved.

  2. #2 NewEnglandBob
    November 25, 2009

    How can there be a neutron star made out of Lamda baryons when they exist for only 10−12 seconds resulting from a proton collision with a nucleus? I thought there were no protons around.

  3. #3 creeky belly
    November 25, 2009

    Not to nitpick, but I don’t think that’s an artist’s rendering of a neutron star. It looks like the Chandra image of the Crab pulsar.

  4. #4 Physicalist
    November 25, 2009

    And there’s no need to have a singularity, it would just be like a plain-old neutron star in every way, except it would be just a little denser than normal.

    Ummm. Not sure I’m following you.

    If we’re talking classical GR and not trying to incorporate any quantum gravitational processes, then if the matter is localized inside the Schwartzschild radius, we’re going to have a singularity.

    Ain’t no force strong enough to prevent gravitational collapse — just like there ain’t no force strong enough to make a perfectly rigid rod.

    Am I misunderstanding your claim?

  5. #5 Physicalist
    November 25, 2009

    Why worry about producing denser matter? If you get enough standard matter at standard densities, it will be contained within its Schwarzschild radius and will form a black hole — with a central singularity.

    For example, if you take 500 million solar masses of water at its standard density, it will form a black hole. (Note that supermassive galactic black holes are thought to be larger than this.)

    Would you want to say that “there’s no need to have a singularity, it would just be like plain-old [water] in every way”?

    Maybe I’m missing your point, but as I read it, you’re wrong on this one.

  6. #6 Mane
    November 25, 2009

    I’ve always wondered, what exactly does a black hole look like in terms of geometry? Like, it’s not really a ‘hole’ is it?

  7. #7 Ethan Siegel
    November 26, 2009

    Physicalist,

    The pressure needed to collapse a nucleon is dependent on the gravitational mass pushing in on it, not the density of the object.

    500 million solar masses is much, much more than enough to collapse any compact object into, at the very least, raw quarks. (For what it’s worth, I imagine there’s probably some kind of gluon soup at the center.)

    But one solar mass under the influence of gravity is not enough to collapse a nucleon, and that’s why I believe the above post is correct.

  8. #8 Physicalist
    November 26, 2009

    The pressure needed to collapse a nucleon is dependent on the gravitational mass pushing in on it, not the density of the object.

    Somehow we’re still talking past each other. Do we agree (a) that if we have a Scharzschild spacetime, all physical trajectories inside the event terminate in the singularity, and (b) that the spacetime in some region will essentially be that of Schwarzschild when we have some given amount of mass contained within the associated Schwarzschild radius?

    If we accept this (and the only way to avoid it, as far as I can see, is to start speculating about quantum gravity), then pressure is a non-issue. Having something “stable” — i.e., not collapsing — inside the event horizon is geometrically equivalent having something traveling faster than light. This just isn’t allowed if we’ve got a classical spacetime. If you don’t want a singularity, you’ve got to postulate some sort of breakdown of the classical spacetime described by GR.

  9. #9 Physicalist
    November 26, 2009

    Should read: “all physical trajectories inside the event horizon terminate in the singularity”

  10. #10 Ethan Siegel
    November 26, 2009

    Physicalist,

    I agree with your “if” statement in part A, but what is it that dictates that the Schwarzschild spacetime in any way describes all (or even any) actual black holes in our Universe?

    Your part B is what I contest. The reason a white dwarf doesn’t go supernova until it reaches 1.4 solar masses is because the atoms at the center don’t collapse until that point. A neutron star has a slightly higher mass limit before the neutrons collapse: perhaps 2 to 3 solar masses.

    But a solid sphere of nucleons has a lot more sophistication going on inside of it than the Schwarzschild spacetime describes, even if it’s a sphere whose radius is smaller than the Schwarzschild radius. And that’s why this holds.

  11. #11 Greg
    November 26, 2009

    Is there any way to tell then, whether a given black hole contains a singularity or some kind of high-density degenerate matter? since we can’t see inside it I suspect the answer is no… is that right?

  12. #12 Physicalist
    November 26, 2009

    what is it that dictates that the Schwarzschild spacetime in any way describes all (or even any) actual black holes in our Universe?

    Well, I guess the fact that it’s a (or “the” in some sense) spherical solution to the Einstein field equations, which demonstrably holds outside of spherical bodies when not much else is around.

    But a solid sphere of nucleons has a lot more sophistication going on inside of it than the Schwarzschild spacetime describes, even if it’s a sphere whose radius is smaller than the Schwarzschild radius.

    Do we agree that outside the sphere of matter the spacetime will Schwarzschild? Inside won’t be, of course.

    If we agree on this, then I fail to see how invoking any classical force can possibly account for a stable sphere inside the event horizon. Look at it this way: it’s geometrically impossible for any part of the sphere to move outward. So we can’t have any outward fluctuations at all. On the other hand, a mere physical force could not prevent inward fluctuations. So there’s no way for the sphere to be stable — it has to contract.

    Now, there may be escape routes by appealing to some quantum feature, but (as I see it) there’s no way we can point to a mere *pressure* to argue that there’s a stable body inside an event horizon.

    Now it’s been over a decade since I’ve been in a GR class, but the literature I’m familiar with takes it as a given that full collapse is inevitable once the matter is contained within it’s Schwarzschild radius. (Think of Thorne’s hoop conjecture, for example.) The arguments over information loss in black holes (for another example) would have taken a very different route if all it took to avoid collapse to a singularity was a sufficiently high pressure.

    Is the possibility of black hole with a stable body inside the event horizon one that is discussed in some literature these days?

  13. #13 Physicalist
    November 26, 2009

    @ Mane (#6):
    You can check out embedding diagrams of black holes e.g. here.

    Some people think of singularities and “edges” or “tears” in spacetime, so there might be something substantial to the label “black hole” since they’re typically thought to contain a singularity (unless I’m mistaken and Ethan’s right). However, several physicists and philosophers argue that this way of thinking about singularities is problematic.

  14. #14 Ethan Siegel
    November 26, 2009

    Greg,

    You are correct; we have no information other than mass, charge, and angular momentum for all black holes. We have no idea whether there’s a singularity or not inside.

    Physicalist,

    When you say “inevitable”, this can often mean an arbitrarily long amount of time. (I.e., the singularity is at future null infinity.) Our entire Universe, if the matter density were about 4 times as large as it is now and was expanding at its present rate, would be on the inside of a black hole. But there would be no singularity at present, nor for the foreseeable next few billion years.

  15. #15 Physicalist
    November 26, 2009

    . . . this can often mean an arbitrarily long amount of time. (I.e., the singularity is at future null infinity.)

    Sorry, I’m not following.

    (i) A black hole singularity is space-like, and (barring evaporation) intersects future timelike infinity. By definition, no point in a black hole is in the causal past of future null infinity, so I don’t see how singularities there can be relevant.

    (ii) I accept your point regarding a possible universe-sized black hole, but I fail to see how this is relevant to black holes that are stellar mass — or even supermassive. It seems obvious to me that once such a mass passes within the event horizon, it isn’t going to be able to remain stable for any appreciable “time.” Can you give me any reason to suppose that arbitrarily long times might be involved?

  16. #16 Greg
    November 26, 2009

    a sort-of opposite exercise: if some physical constants were different, would it be possible to envisage a universe in which neutron stars were also hidden behind event horizons?

  17. #17 csrster
    November 26, 2009

    I may be out of my depth, but don’t the Penrose-Hawking theorems guarantee a singularity for any Black Hole (under reasonable assumptions) ?

  18. #18 ScentOfViolets
    November 26, 2009

    I suspect very, very strongly that Physicalist is correct. Inside the event horizon, all trajectories must point towards the ‘future’, i.e., towards the center of the black hole. That’s just geometry. Another way to think of it is in an information-theoretic sense: to keep the whole kaboodle from collapsing, there must be a counter-pressure exerted outwards. But this is equivalent to traveling faster than light, since this necessarily entails information being communicated away from the center. Since this is impossible according to SR, there can be no such pressure.

    Now, in a Newtonian universe where the speed of light is not an upper limit, black holes without singularities are certainly possible. But with that extra caveat (and without invoking some sort of QM effects), I don’t see how singularities are avoidable.

  19. #19 Ethan Siegel
    November 26, 2009

    Well, I went back and looked, and it looks like you guys are all talking about the standard analysis, which they assume “pressureless dust” for. I am not convinced the same arguments hold when you have a strong degeneracy pressure internally.

    If you can tell me how a one-solar-mass neutron star would have a different net force/pressure at its core from a one-solar-mass bottom-neutron star, then I am open to the possibility that these baryons will indeed collapse. But as far as I can tell, you don’t overcome the degeneracy pressure with such a small amount of mass.

  20. #20 Nick
    November 26, 2009

    So what is the astrophysical definition of a (Black Hole) singularity. Or are they purely mathematical?

  21. #21 Physicalist
    November 26, 2009

    It’s certainly true that we usually work with dust b/c it’s easier, but it’s well-established (I’m confident) that the basic point generalizes. I don’t have my books here to give you references, but csrster’s point (#17) is a good one: If you aren’t denying one of the premises of the singularity theorems, then you’re not giving us any reason to believe that we might avoid a singularity.

    If you can tell me how a one-solar-mass neutron star would have a different net force/pressure at its core from a one-solar-mass bottom-neutron star . . .

    I suggest that we don’t want to be looking at the core, but rather at the event horizon. Again, I find it helpful to think of a supermassive black hole formed from a huge volume of water at standard density. When that volume reaches the Schwarzschild radius, there’s no physical way to get it to expand again — it’s a one-way street. But we don’t (at that point) have any impressive pressures at all.

    Likewise, the relevant question with our neutron star and bottom star is what’s going on at the event horizon? Notice that to remain stable with a surface just outside the event horizon, you’d need forces that are equivalent to incredible accelerations. (Imagine yourself standing the surface of a neutron star.) This is reinforced by considering Rindler spacetime, which is mathematically equivalent to the exterior of a black hole for our purposes. You can accelerate up to the light cone, but you can never cross it.

    Then the point is that because the outside of the bottom-neutron star is unable to support itself, it will inevitably crash down on the interior matter, and pressures will presumably increase without bound (though I’m not sure pressure is well-defined in the presence of a singularity . . . )

  22. #22 Physicalist
    November 26, 2009

    Just to reiterate/reinforce the comparison with a rigid rod: Even though spacetime is only Schwarzschild outside the matter, to have a stable body inside the event horizon, the force at the outside edge of the body (where Schwarzschild begins) would have to be so great that it could be used to send superluminal signals in normal contexts. This just won’t fly. It’s basically like trying to keep an object straight in a curved space — it’s geometrically impossible.

  23. #23 ScentOfViolets
    November 26, 2009

    Exactly, Physicalist. If there were whales moving underneath the surface, we could detect their presence by pressure variations at the surface(if that’s too fanciful, imagine someone on the other side of the star pounding on the ground with a sledgehammer.) In any case, this amounts to sending information faster than light.

  24. #24 Derek Lee
    November 26, 2009

    I really think Physicalist is right on this one. Outside the star, the geometry is Schwarzschild; if the star’s radius is less than the Schwarzschild radius, a light ray inside the radius would follow the same trajectory as if it were a singularity, not a star. That light ray would, if it were a singularity, reach r=0 in a finite, small, amount of time. Any particle on the surface of the star is within the light cone at that radius, so the surface has to collapse within that amount of time. All of this is independent of the solution inside the star, you only assume that the exterior is Schwarzschild.

  25. #25 ScentOfViolets
    November 26, 2009

    I should also point out that the whole ‘universe inside a black hole’ idea is misleading. IIRC, the boundary conditions for a Schwarzschild hole have a flat spacetime at infinity. The same cannot be said for the ‘universe inside a black hole’ notion, and that is why(without going into any details here) you can send signals back and forth the width of the universe ‘inside the black hole’. That is, the analogy is not a good one to extrapolate from in this particular instance.

  26. #26 Eric Lund
    November 26, 2009

    I’m going to speak up in Ethan’s defense here. I don’t know for sure that he’s right, but I am not satisfied with the objections Physicalist et al. have raised. It’s not possible for any information to escape the Schwarzschild radius because nothing can go faster than c. That does not mean that information cannot propagate radially outward, as long as there is no communication from a point inside the Schwarzschild radius to a point outside–since its velocity is less than the escape velocity, it will eventually fall back. Quarks are fermions, so you can have a spherical shell supported against gravity by the degeneracy pressure of the spherical shell below. And once you are below the surface of this neutron star, gravity should actually decrease because some of the mass is in a spherically symmetric configuration above you. The only assumption Ethan needs is that the degeneracy pressure of Λ baryons is at least as large as the degeneracy pressure of neutrons. Of course, there is also the question of whether this configuration is stable to deviations from spherical symmetry.

  27. #27 slw
    November 26, 2009

    I would like to point out that the observable universe is technically a black hole ;)
    3*10^53 kg is the required mass to form a black hole with the Schwarzschild radius of the observable universe(4.65*10^10 ly), if dark matter/energy measurements are correct then the observable universe has mass of almost twice that.

  28. #28 Physicalist
    November 26, 2009

    Eric Lund says,

    That does not mean that information cannot propagate radially outward, as long as there is no communication from a point inside the Schwarzschild radius to a point outside.

    If we’re talking about the spacetime geometry of the vacuum outside a spherical mass, then then there is indeed a prohibition on information propagating radially outward inside the event horizon. The speed of this propagation would have to be c at the event horizon, and inside the event horizon it would have to be even higher. It’s the overall geometry that’s important here; the event horizon is just one part.

    Now it’s true that inside the matter itself there’s no prohibition on outward propagation. Indeed, if we consider a spherical shell of matter, the interior spacetime will be flat (Minkowski) spacetime, so there’s no problem moving any which way you like — until the shell falls on you, that is.

    But the relevant question is whether it’s possible to have the the matter form a stable sphere inside the event horizon (e.g., whether it’s possible to have that sphere sit at a fixed distance from the center). For the reasons given above (including the singularity theorems), we should think this isn’t possible.

    . . . you can have a spherical shell supported against gravity by the degeneracy pressure of the spherical shell below. . . . The only assumption Ethan needs is that the degeneracy pressure of Λ baryons is at least as large as the degeneracy pressure of neutrons.

    No, this might be true if spacetime were Newtonian (I’d have to give it more thought), but it clearly is not true in the spacetime of General Relativity.

    I think pressure is a red herring in this context. The relevant question is what force would be required to accelerate the matter sufficiently to have it escape the black hole that is forming. As you approach the event horizon (from outside), the relevant acceleration goes to infinity. Once you’re inside, there is no acceleration that will get that bit of matter back to the outside universe. This means that there’s no force that can provide this acceleration. Collapse is inevitable.

  29. #29 ScentOfViolets
    November 26, 2009

    Eric@26: If this is true, then you have a prescription for unblackening a hole(well, some of them): Find a strange-matter star that is just within a nanometer of its Schwarzschild radius so that it is just ‘barely’ a black hole. Now pour a couple of hogsheads worth of neutrons on top. Presto! A lower average density, and a star with a neutronium crust that is larger than it’s Schwarzschild radius. Are we all agreed that once a black hole is formed, it’s impossible to escape from them? So there appears to be a contradiction here.

  30. #30 Physicalist
    November 26, 2009

    It occurs to me that it might be helpful to point out a difference between Newtonian black holes and relativistic black holes. In the Newtonian case, even though the escape velocity is above c, one could escape from the body using a rocket. Think of it this way: you shoot something as high as it will go, and even though it doesn’t escape, it can get quite high before it starts falling back. Then, at the top of its arch, have it shoot some part of itself higher, . . . and so on. (Or, for that matter, you could just build a really high tower . . . ) Newtonian black holes aren’t one-way streets.

    Relativistic black holes are obviously quite different. The event horizon is a one-way street. This means that even a rocket can’t get out, and it also means that you can’t build a tower to escape. If there really could be a stable sphere inside the event horizon, it would seem possible to build a ladder to escape. Obviously relativity rules this out.

  31. #31 Geoff Ryan
    November 26, 2009

    I just did a quick search about degeneracy pressure, and it seems that when the mass limits are calculated, something approximately schwarzschild is assumed for the metric. Since the Schwarzschild metric is only valid outside the Scwarzschild radius, wouldn’t this mean that the mass limits are only valid for stars larger than Rs ?

    So since the bottom-quark star fits inside it’s Schwarzschild radius, you wouldn’t expect the quark degeneracy mass limit to apply, and since you now have a big ball of matter inside a schwarzschild black hole, it would promptly undergo collapse and form a singularity.

  32. #32 Physicalist
    November 26, 2009

    Just a quick historical note in reply to

    In 1916, everyone assumed that whatever happened inside a black hole, it must be powerful enough to simply destroy everything inside of it, and crush everything down to a singularity.

    If I recall, early on people thought that the r=2M singularity (i.e., the coordinate singularity at the event horizon) was a real singularity. They didn’t think that a star could collapse past the Schwarzschild radius. Picturing the situation in Schwartzschild coordinates, they believed that everything would freeze at it collapsed to r=2M (thus folks referred to collapsed stars as “frozen stars”).

    I’d need to double check, but wasn’t it only with Kruskal in 1960 that people started looking at the interior of black holes at all? Keep in mind that Wheeler’s term “black hole” wasn’t coined until the 60s.

  33. #33 MadScientist
    November 27, 2009

    Do black holes dissipate – or if they were not observed to dissipate is there some mechanism that allows them to? Otherwise if everything can go in but can’t come out, aren’t they destined to grow indefinitely as they get near other matter? (Well, except that they can’t chase other galaxies due to the expanding universe.)

  34. #34 Eric Lund
    November 27, 2009

    SoV @29: No, that technique doesn’t work. The Schwarzschild radius is proportional to M, but the radius of our hypothetical lambdonium (or whatever you want to call it) star is only proportional to M^1/3. So if it starts on the edge of being a black hole, adding more mass pushes it further into being a black hole. Even if the crust is ordinary neutrons here, it won’t decrease the density fast enough.

  35. #35 Geoff Ryan
    November 27, 2009

    MadS @33: Yes, Hawking Radiation! Stephen Hawking found in 1976 that near the horizon of a black hole particles will be spontaneously created from the gravitational field. Some of these particles will escape and in so doing will steal energy (ie. mass) from the black hole. The process is called Hawking Radiation, and causes black holes to evaporate over time. One of the neat things is that the rate of evaporation is inversely proportional to the mass of the hole, so small holes will evaporate very fast. This is one of the many reasons no one is worried about black holes at the LHC, because they will be tiny, and evaporate almost instantaneously.

  36. #36 ScentOfViolets
    November 27, 2009

    Eric@34: I perhaps didn’t explain myself very well. The point is that a single neutron can ‘stick out’ above the event horizon if the horizon is barely above the surface of the actual material. Ah, I see it: the radius of a neutron is a fraction of a nanometer, not vice versa. My apologies. I should have said a fraction of a Fermi, 10^-15 m, not a nanometer, 10^-9 m.

  37. #37 BenHead
    November 27, 2009

    The parts of this discussion that I’m able to understand are really fascinating, but I also find the necessary disclaimer in Physicalist’s case, “If we’re talking classical GR and not trying to incorporate any quantum gravitational processes…” to be a sticking point. Isn’t degeneracy pressure an inherently quantum phenomenon? I mean, the behavior of subatomic particles under the intense gravity one would find within a black hole are exactly the sort of thing we CAN’T currently talk about with certainty without a working theory of quantum gravity, right?

  38. #38 Nathan Myers
    November 28, 2009

    Pick a sphere at r=0.5R, at the moment t when enough mass has accumulated to form a black hole with radius R. The mass inside that radius is not itself enough to form a black hole, and all the mass outside it doesn’t count. Walk r outward. It’s the same even at R-ε. The interior of a black hole isn’t necessarily a black hole.

    Physicalist, what’s wrong with this?

  39. #39 Geoff Ryan
    November 28, 2009

    BenHead @37: You’re right, if we wanted to figure out the full dynamics of this type of system, at some point we’d need a full theory of quantum gravity. However, it turns out there still are things we can say about the system with the theories we have now, and degeneracy pressure (and Hawking radiation) are a couple of these things.

    General relativity has two parts 1) Space is curved, and this curvature affects how matter behaves, and 2) The curvature of space depends on where the matter is. When we try to make a quantum theory of gravity, #2 is the part that gives us trouble, figuring out how curvature changes in response to quantum matter is not easy at all. However, we can do #1 fairly well! People have written out quantum mechanics in curved space, and have used this to make predictions (this is how Hawking Radiation was developed). Essentially we assume the curvature is fixed, and won’t change in response to the matter for short periods of time.

    Degeneracy pressure and just about all of our information about black holes come from this idea, that we can more or less introduce quantum effects into a gravitational system, as long as we are careful about it. I’m assuming Physicalist was more talking along the lines of string theory or loop quantum gravity with his disclaimer there, although I could also be completely wrong.

  40. #40 Physicalist
    November 28, 2009

    Nathan Myers asks what’s wrong with this:

    The mass inside that radius is not itself enough to form a black hole, and all the mass outside it doesn’t count. Walk r outward. It’s the same even at R-ε. The interior of a black hole isn’t necessarily a black hole.

    I’m not sure I follow the example, but I believe the answer to your question is that we need to be more careful about what is meant by a “black hole.” The usual definition is a region of spacetime from which light cannot escape “to infinity.” (Note that this notion requires that there is an “infinity” to escape to. When the spacetime is asymptotically flat, there’s no problem, but in other situations the notion becomes tricky. This is why, for example, it can be misleading to say that “the observable universe is technically a black hole” as in #27.)

    Given this definition, it should be clear that we shouldn’t say “the mass outside [some region] doesn’t count.” The only relevant question is whether it’s possible to escape from some region (all the way out to infinity) without going faster than light; clearly in your example this isn’t possible, so everything inside the exterior collapsing matter is indeed a black hole.

    Now it is true that it’s possible to be inside a black hole and have absolutely no indication of this (for a time). Suppose, for example, that many extremely high-energy gamma rays were converging right now on the Sun. We could be in a black hole (in the above technical sense) long before these gamma rays came near us. We might, for example, be in a black hole when they passed the orbit of Pluto. What this would mean is that any light signal we sent out after that moment wouldn’t escape outside our solar system. It might, let’s say, make it as far as Jupiter, but by that point the incoming gamma rays would be at Jupiter and the resulting gravitational curvature would prevent the light from escaping. It would be even longer until the gamma rays passed the orbit of the Earth, and if they missed us, we might not even notice their passing; but it would then be impossible for us to move farther from the sun. At that point we would, of course, be drawn inexorably towards the Sun and the resulting singularity, until we were torn to bits.

    This is just a long-winded way of articulating the point I made in #28: the spacetime inside of the contracting matter needn’t be highly curved — indeed, it will be flat if the matter is hollow in the middle. But even though the spacetime in that region is flat, that flat region is still contained within a black hole. And (according to our current physics) there is no way to stop the matter inside an event horizon from contracting, so less and less of the interior will be flat as time goes on.

  41. #41 Physicalist
    November 28, 2009

    I’m assuming Physicalist was more talking along the lines of string theory or loop quantum gravity with his disclaimer there

    Yes, or some other theory of quantum gravity. But I’d actually want to think a bit more about how degeneracy pressure works before I asserted too confidently that there’s no quantum wiggle room there.

    This much I feel is safe to assert: If degeneracy pressure can sometimes be overcome by gravitational forces (e.g., when you have 50 solar masses of neutrons), then it will definitely be overcome inside the event horizon of any black hole.

    It’s worth pointing out, with respect to quantum wiggle room, that quantum field theory in curved spacetime violates the standard premises of the singularity theorems (specifically, the positive energy requirement, I believe). This is why black holes can shrink through Hawking radiation, even though this is forbidden by the area increase theorem. So there might be some quantum escape from a singularity even short of quantum gravitational theories like string theory and loop quantum gravity. But I know of no actual proposal along these lines.

  42. #42 Solar
    November 30, 2009

    Wow, that’s so cool. I thought that all black holes had a singularity. That’s so weird to think about a star that doesn’t emit light and I’m assuming doesn’t emit heat as well? I suppose I don’t understand how the whole process works. I would think that if the star stopped emitting energy, then it would continue to grow in mass until it eventually formed a singularity. I’m no scientist though, so I’m sure I’m missing something. Thanks for the really intriguing article!

  43. #43 alexandru
    December 1, 2009

    I have a question: if a black hole as described in this post accumulates enough lighter mass can it become a neutron star, or something that is not a black hole anymore?

  44. #44 Thomas Neil Neubert
    December 5, 2009

    Ethan’s challenge “If you can tell me how a one-solar-mass neutron star would have a different net force/pressure at its core from a one-solar-mass bottom-neutron star, then I am open to the possibility that these baryons will indeed collapse. But as far as I can tell, you don’t overcome the degeneracy pressure with such a small amount of mass.” is a bogus challenge for two reasons:…. Because..

    First, the net gravitational force at the center of any spherical symmetric object (e.g. neutron star or planet made from marshmallows) is zero. There is no gravitational force at the center of his hypothetical bottom lambda neutron star; but I don’t see that that implies anything. And since the surface area at the center is zero; then also the
    force/pressure = area = zero
    at the center of a sphere of marshmallows or a lambda bottom neutron star. I’m of course talking about and using equations from classical mechanics; but then Ethan insists on saying nothing about general relativity.

    And as Ethan well knows, Einstein’s general relativity’s equations (just like Newton’s equations) do not say anything about the type of matter involved in their equations of gravity.

    And second Ethan’s challenge is bogus because as he well knows a typical neutron star is not supported from collapse by force/pressure at its core; rather a neutron star is supported from further collapse by the Pauli exclusion principle which does not allow two neutrons to occupy the same quantum state. So inside the event horizon of a black hole (if we believe general relativity)a neutron star composed of neutrons or lambda bottom particles will continue to collapse beyond where the Pauli exclusion principle suggests that it is impossible to collapse.

    By the way, I don’t accept the above standard explanation that I’ve just give. But here is not the place to discuss other fringe hypotheses.

    So in my mind, Ethan’s hypothetical Lambda bottom neutron star, tells us nothing about whether there is a singularity or not. And furthermore, since lambda bottom baryons do not appear to exist in abundant quantity in the so far observed universe; his hypothesis (to me) seems to be mostly of interest as a possible phase transition as a larger real neutron star of sufficient mass shrinks below the event horizon of a black hole. Ethan’s hypothesis seems to suggest that the energy to compress quarks might cause down quarks to convert to bottom quarks. This is an interesting and I assume testable hypothesis. Testable not I assume by astronomy; but testable perhaps by elementary particle physicists. I defer to the opinions of astronomers and elementary particle physicists as to my “testability” remarks.

    Acknowledging that possibility (implied in Ethan’s hypothesis); I would ask Ethan to reconsider his hypothesis that nothing happens to an astronaut passes through the event horizon of a large black hole. You seem implicitly to suggest that the down quarks in normal neutrons (e.g. of the human body) begin to phase transition into bottom quarks as an astronaut passes through the event horizon of a black hole. I don’t think such a human body would be viable.

    OK I’ve speculated enough. But Ethan’s question is a red herring and I think he knows it. I don’t think that he is suggesting that any astronomer will observe star full of lambda bottom baryons before collapse beneath the event horizon of a black hole. And I don’t think that he is suggesting that after collapse that such a hypothetical lambda bottom black hole could be distinguished from any other black holes. Just like any other black hole a lambda bottom black hole would gobble up any kind of matter (e.g. astronauts, planets, stars and even merge with other black holes; and would thus grow in observed mass.

  45. #45 David Marjanović
    December 16, 2009

    How can there be a […] star made out of Lam[b]da baryons when they exist for only 10−12 seconds

    The same way neutron stars exist even though free neutrons have a half-life of just under 15 minutes: radioactive decay can be prevented by sheer brute force. Free neutrons decay into a proton, an electron, and an antineutrino; neutron stars form when the pressure of a collapsing star squeezes the electrons into the protons, forming neutrons and neutrinos.

    Incidentally, I don’t know how a neutron star could turn into a lambda star. By uptake of neutrinos or something???

    we have no information other than mass, charge, and angular momentum for all black holes.

    I’ve read that entropy is directly proportional to the area of the event horizon. What happened to that idea…?

    If there really could be a stable sphere inside the event horizon, it would seem possible to build a ladder to escape.

    Not using real matter. On Earth, a mountain cannot become taller than about 10 km because it would collapse under its own weight. On a neutron star, a mountain cannot become taller than about 10 cm because it would collapse under its own weight…

  46. #46 David Marjanović
    December 16, 2009

    What? Why am I signed in? That’s not even supposed to be possible on this blog, is it?!?

    BTW, I do not have a blog. Vox.com just forces me to pretend so that I can register at all. I had to register for Pharyngula, and the other options are all said to be horribly unreliable.

  47. #47 David Marjanović
    December 16, 2009

    Sorry, not 10 cm – 5 mm.

  48. #48 physicalist1
    December 17, 2009

    @ David M:

    we have no information other than mass, charge, and angular momentum for all black holes.

    I’ve read that entropy is directly proportional to the area of the event horizon. What happened to that idea…?

    A classical black hole is characterized completely by mass, charge, and ang. momentum. It is only when we apply quantum mechanics to a black hole that we can assign an entropy to it.

    Black hole entropy is still not well understood, but it is a surprising consequence of expanding the laws of thermodynamics to account for the Hawking temperature of black holes. Some theories of quantum gravity (e.g., loop QG, and string theory) have been able to offer a counting of quantum black hole states that are consistent with a statistical account of black hole entropy.

    If there really could be a stable sphere inside the event horizon, it would seem possible to build a ladder to escape.

    Not using real matter.

    The point is that you can’t use real matter to form a stable sphere inside the event horizon. The same line of reasoning that rules out ladders also rules out stability for the bottom neutron star that Ethan postulates.

    Here’s the decisive point:

    Look at the outer surface of the proposed neutron star and ask what forces would be required to prevent a particle from falling inward. If the star is contained inside its event horizon, then the answer is that an infinite force is required if the particle lies the least bit above the sphere of matter. This means that there is no way such a sphere can be stable; the slightest fluctuation inward will inevitably lead to further collapse.

  49. #49 akshay jha
    November 2, 2010

    can i get the e-mail address of this scientist, i would like to ask him a question that:
    “can we create the complete condition that is around blackhole on earth or in space?”

  50. #50 akshay jha
    November 2, 2010

    why can’t we trawel towards the past time?

  51. #51 Jack Tanner
    November 12, 2010

    @physicalist1

    “Look at the outer surface of the proposed neutron star and ask what forces would be required to prevent a particle from falling inward. If the star is contained inside its event horizon, then the answer is that an infinite force is required if the particle lies the least bit above the sphere of matter. This means that there is no way such a sphere can be stable; the slightest fluctuation inward will inevitably lead to further collapse.”

    Can’t this also be stated that for every point inside the event horizon the light cone is tilted inwards? Hence, every geodesic leads to a singularity. I thought that the Penrose-Hawking singularity theorem stated that some kind of gedesic incompleteness (singularity) exist inside any black hole, assuming a non-negative energy desity.

  52. #52 Clark
    November 18, 2010

    I keep reading that there are different sizes of Blackholes dependent upon it’s mass. If a black hole has infinite mass, then regardless of how much more mater falls into the Blackhole, it will always have the same amount of mass; Infinate. As such, the event horizon should be the same distance from the singularity of all black holes, thus providing a distortion radius the same at all Blackholes. Thus if you’ve indirectly seen one, you have indirectly seen them all.

  53. #53 $$$$
    December 6, 2010

    I think that you claim is a very valid one, but sadly is utterly false. Once you force neutron star down to the radius of 3km, the gravitational force would cause it to collapse, further, in on its self, and there would be nothing you could do to stop it. The neutron star would do what any neutron star would do in that situation…become an infinitesimally dense point, that we all know as a singularity. I think you are confusing the singularity with the event horizon, as it is the event horizon from which nothing can return, not the singularity. It is the event horizon that causes the blackness. A black hole without an event horizon would be a slightly more supportable claim. But then it wouldn’t be a black hole, because its fastest escape velocity could only be the speed of light. But since a neutron star collapses bast this point, and does not stop, it is impossible for either of our idea to exist. But your thinking, trying to bend the rules…and I admire that.

  54. #54 Blint
    December 7, 2010

    Well, I went back and looked, and it looks like you guys are all talking about the standard analysis, which they assume “pressureless dust” for. I am not convinced the same arguments hold when you have a strong degeneracy pressure internally.

    The Penrose-Hawking singularity theorems do not assume “pressureless dust”, they assume either the weak energy condition (positive mass) or dominant energy condition (no superluminal flows). As the “lambda star” is a mostly static clump of heavy baryons, it falls well inside the theorems’ range of applicability.

  55. #55 akshay jha
    December 31, 2010

    Does antigravity exist?

  56. #56 Michael Churvis
    March 14, 2011

    Yes. The force of Gravity has a repulsive element, as is shown by galaxies’ repultion of one another.

  57. #57 Akame
    May 22, 2011

    If an object has enough mass to create an “event horizon” then wouldn’t it be safe to assume that any known force that could possibly give the object volume isn’t strong enough to overcome gravity and the object would collapse into a single point.

    I’m no physicist, but many say that the standard laws of physics would’ve broken down within the event horizon. If this is true than how is it possible to truly know what’s inside the event horizon?

    Gravity is described as a dent in space-time. If the previous statement is true than time within the event horizon would’ve all but stopped. This would mean that the moment the event horizon is created, the mass within it would be “collapsing” into a singularity forever.

    Again, I’m no physicist and I don’t have any math to back up my assumptions but I can’t help but feed my curiosity.

  58. #58 Adnan Sakli
    January 22, 2012

    Thee entire problem is that all of the theories are based upon constants to the human animal and it´s observations.
    Fact, time does not exist, it is a measurement of humans. So it is not a real form of a tool to scale against. Presence does exist , but in what form and how is it able to expand and collapse or evolve.
    So we as humans are variables that do not have a major effect upon existence or reality.
    All substances are fluid. The degree of fluidity depends on the movement of the recognized structures of the atoms..
    The universe exist in a constant primary harmonics and sub harmonics it is the sub harmonic that we are in , or our recognized universe is in as per our perception.
    These sub harmonics are pulled apart by outside effects of greater harmonics or interaction of the primary harmonics.
    This creates the tubular cones . As they travel or are being stretched they appear to be diminishing from point center or origin. This would make it appear as an cone. since there are always positive and negative actions , the cones are in a repelling and pulling motions . At a given point of separation the core starts to collapse onto itself and the two opposites start to move toward each other where the two most distant ends meet on the inside of the cone like a donut and the two most distant points meet. This meeting causes the reaction of impact and they pass through each other. now you have the two separating again in the opposite direction to to a point where they turn again. Now this point has the reaction of the two bases being pulled apart causing the separation of the fields to new a new smaller cycle or reconnecting to repeat the process.
    The outer point of the cone has the ability to act in two ways as well . One would be to fold inverse or to open the end to an dispersion. At the dispersion point the energy fields would split and find reconnect with other cones or tubes that have the similar or counter fields. as they are connecting with the fields they are free flouting tubes that appear as strings.once they connect up with the counter field they start to build a new and different resonance field , based upon the variation of size and environment.
    The most important interaction element is sound a , because sound is the creation of the resonance field the is created by the variation of the energy fields . So in essence the interaction of the variations can and will cause reactions to varies fields to act in desired or controlled environments. Once the reaction points are logged in reality sound can be used to cause chemical and physical reaction to the formulation of new and existing energy fields that can duplicate any and all matter with in our grasp of thought .
    Now the point that is not to be determined is the point of evolution to a point where energy morphs to an different element and causes a reaction point in a compounded format. This causes the evolution process that we have no idea about as it is the formation of a field that is beyond our event horizon and our point of realization structures change, much like the splitting of a cell to form a whole that exist beyond our existence.
    Hence the 14 dimension, the evolution of our reality to something greater then us and the universe as we know of. Where all the learned processes are rewritten and a whole new structure exists.
    So in essence the theory that the universe is being pulled apart is correct and at the same time the fact that the universe is collapsing is correct because the two are the description of the reactions of the linear energy cones and the formation of strings and the formation of new fields.
    This happens contiguously and at varied levels. The field we see as Black holes are the in versing of the the energy cones to a point where the two opposites meet and move forward to the reactions as described.
    The big question id why they act in the circular pattern, I can only presume that it is the only pattern the is equal at all points making the reaction constant at all levels. Much like the funnel of water at a point of drainage. The reactions depending on the fields of energy are clockwise and counter clockwise at the opposite side and the meeting point is the ocean of life or in this case the universe as we know of it .
    The universe does not react to us , we react to the universe and in relation we are just segmented portion and at the same time we are multivariate in our cellular formation and the ability to interact with the universe and it normal actions..

    Theory and reality . All answers are correct and wrong based upon the variation of the reality of our perceptions and the natural relations to the existence as we know it .

  59. #59 margarita
    berlin
    August 29, 2012

    Hello, I just wanted to say a big thank you, for explaining it in such simple yet beautiful worlds.
    I don’t have a clue about physics, unfortunately, since I’m a writer, but I’m doing some research for a literature project I’m currently working on. I’ve always been fascinated by astrophysics – let’s say in a philosophical way – and I try to understand as much as I can. It’s breathtakingly beautiful and scary at the same time. Thank you very much! It’s such terrible, ignorant rubbish when those idiots are asking “Why spend so much money on astronomy research? Aren’t there enough problems to solve on earth?” I am so glad and grateful that there are people in this world who have enough brains, curiousity and guts to dare looking at the stars and answer the really important questions of our time. Sorry for this confused letter of awe…I just think science needs much much more appreciation. the warmest greetings from germany! m.

  60. #60 Philip Greener
    United States
    December 26, 2012

    I think you explained something very true. Perhaps, all black holes are not ‘black holes’, but a spectrum of extreme power and not-as-much-but-still-extremely-powerful gravity wells. By definition I believe a black hole is not infinite (science has proved no infinities, yet–I’d say consciousness is). The fact you made a distinction here proves ALL black holes are nothing ‘special’ or ‘unique’ but closer to an imagined infinity than most other things we have found. Point is, lots of things escape ‘black holes’ in its jets.