Ask Ethan #88: Where is the Cosmic Microwave Background? (Synopsis)

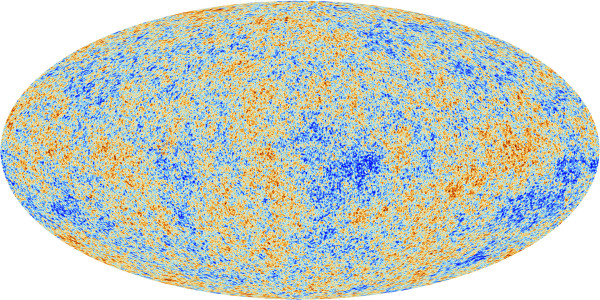
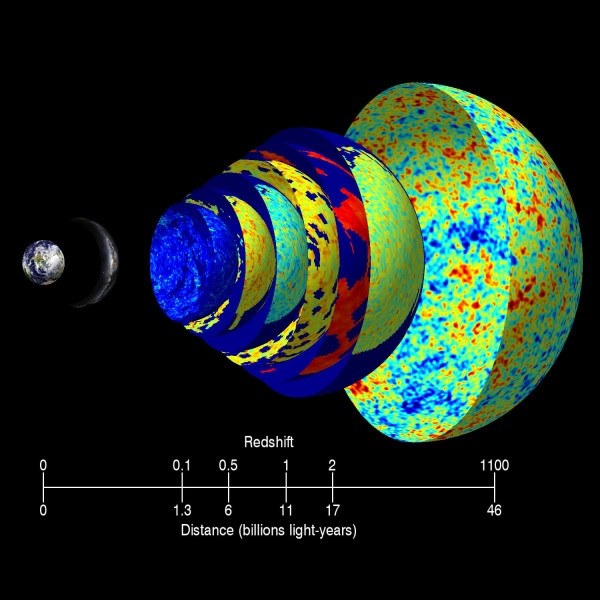
Ethan, in your post you write, "We actually have sufficient evidence that the CMB’s temperature was hotter in the past; as we look to higher and higher redshifts, we see exactly this effect."

How do we see that? I don't mean the plot you posted, but rather, how are the data points themselves acquired? Do you look for "blackbody shaped" spectra associated with the spectra of objects observed at various redshifts?

The thing about the CMB I don't get is why it changes. It was even mentioned in the article that if the dinosaurs had microwave telescopes they would have seen a different CMB.

If we are looking back in time to the point of reionization, why would a dinosaur have seen something different if it were also looking back in time to the point of reionization?

If dinosaurs had telescopes, they would have seen older CMB. If the CMB changes over time, then they would have seen a different CMB. Just like they saw different continents, despite us being able to walk on the continents today.

Where, precisely, is your confusion there?

@Wow #3

It is probably the verbiage. I get the impression the CMB is like a wall. It represents the earliest point in time we can use photons to image, and that limitation is due to the technology we have combined with the conditions that existed that far back.

The conditions that existed in the universe at 380,000 years after the BB are now locked in history. I have a hard time understanding why a dinosaur looking at a point 380,000 years after the BB would see something different than we see looking at 380,000 years after the BB.

Is it because we are not really looking at a point 380,000 years after the BB but rather the photons released at that point are acting like a backlight on an LCD screen? The backlight is what it is, but history of the universe sitting between the backlight and us is different than it would be for the dinosaur. Is that it? Or am I misunderstanding what the CMB is?

"It is probably the verbiage. I get the impression the CMB is like a wall."

Well, what gives you that impression, such that you think it must conclude that the dinosaurs wouldn't have seen a different CMB?

I ignore the "verbiage", it's irrelevant.

What makes you say that the BB was locked in 380,000 years after the inflationary period ended?

"the photons released at that point are acting like a backlight on an LCD screen?"

YES.

The problem is that your claim here:

"Is it because we are not really looking at a point 380,000 years after the BB "

Is something you've manufactured as an issue. I have no idea why you think that causes the alternate to "LCD screen". Are you thinking that this CMB should be from 380,000+65,000,000 years after the big bang?

No, it shouldn't.

The amount of "universe" we can still see from 380,000 years after the big bang is different from the amount of "universe" the dinosaurs could still see 65,000,000 years ago.

The stretch of photons has increased, redshifting the photons even further.

(Michael, this would be why the CMB is cooling, too. *Evidence* for it was beyond the level I was at when I stopped being involved in academia)

So in two ways what the CMB shows now is different from what it showed 65,000,000 or 125,000,000 years ago.

We DON'T get to see the exact same photons every time. Once we've detected it, that photon is GONE, never to be again. Any further light will have to have been emitted at a later date.

Remember, too, that photon redshift will also cause "time to slow down". At the very extreme, where the redshift is near infinity, the time slow down is such that a nearly infinitesimal time has passed between the age of the universe at that spot in space when we look at it now compared to if we'd looked at it a billion years ago.

Remember too that the CMB isn't a flat wall. It has depth. The disassociation took time. And redshift combined with expansion means that time elapsed is seen as distance from us.

"It is probably the verbiage. I get the impression the CMB is like a wall."

Well, what gives you that impression, such that you think it must conclude that the dinosaurs wouldn't have seen a different CMB?

I ignore the "verbiage", it's irrelevant.

What makes you say that the BB was locked in 380,000 years after the inflationary period ended?

"the photons released at that point are acting like a backlight on an LCD screen?"

YES.

The problem is that your claim here:

"Is it because we are not really looking at a point 380,000 years after the BB "

Is something you've manufactured as an issue. I have no idea why you think that causes the alternate to "LCD screen". Are you thinking that this CMB should be from 380,000+65,000,000 years after the big bang?

No, it shouldn't.

The amount of "universe" we can still see from 380,000 years after the big bang is different from the amount of "universe" the dinosaurs could still see 65,000,000 years ago.

The stretch of photons has increased, redshifting the photons even further.

(Michael, this would be why the CMB is cooling, too. *Evidence* for it was beyond the level I was at when I stopped being involved in academia)

So in two ways what the CMB shows now is different from what it showed 65,000,000 or 125,000,000 years ago.

We DON'T get to see the exact same photons every time. Once we've detected it, that photon is GONE, never to be again. Any further light will have to have been emitted at a later date.

Remember, too, that photon redshift will also cause "time to slow down". At the very extreme, where the redshift is near infinity, the time slow down is such that a nearly infinitesimal time has passed between the age of the universe at that spot in space when we look at it now compared to if we'd looked at it a billion years ago.

Remember too that the CMB isn't a flat wall. It has depth. The disassociation took time. And redshift combined with expansion means that time elapsed is seen as distance from us.

The image of wall is, I believe, entirely one you made yourself.

You need to stop wondering what science got wrong and start wondering if you got it wrong.

AFTER you've checked that out, THEN you can wonder if science got it wrong.

This is one reason why "Science got it wrong" really only meaningfully comes from those specialists in the same field as the area being claimed wrong: they have to know that they understood the science correctly FIRST. Otherwise the error isn't in the science, it's in the one "understanding" and claiming it wrong.

Remember too that an LCD emits light from within a depth.

What you claim on an LCD to be a flat screen is rather a deep well that emits light throughout that depth.

@ WOW #6
A minor correction with the LCD - the liquid is only polarising the light passing through it. In itself, it emits nothing. Without a backlight, the screen may be seen by the action of scattered light from other sources.

Aye, but that part of the LCD

a) is still of depth
b) is darkening, not lighting, therefore cannot be extracted from the term LCD in this case of photons being seen.

IOW, that's not only pedantic, is pedantically incorrect itself.

To remember, too, when light passes through a medium, that medium intercepts the photon, destroying it, and in the process emits another photon.

This is how you can get light traveling through a medium slower than the speed of light: the photons still travel at light speed butt, the overall pattern is not. It keeps getting interrupted on its journey.

I insist that the spelling mistake of but was not Freudian...!

Your parapraxis is so telling.

I assume the "surface" we are seeing in the CMB, is like the surface of a very tenuous fog, some of the photons will be older ones, that were just lucky enough not to be scattered, and some will be a bit younger than average too. So we aren't seeing a surface, but rather a vast foggy region.

So Kevin, I presume because millions of years ago (or from a different point in the universe, they are seeing CMB photons from different portions of space. Presumably theory predicts on what time scale the fluctuations change (to a stationary observer)?

Now, for another question, why did we end up with mostly Hydrogen some Helium and tiny amounts of Be,Li, but not mostly Iron-Nickel? The universe was once much hotter and denser than needed for fusion, but the nucleons obviously didn't combine into heavy elements before things cooled off enough to freeze the atomic composition. So why was it the light elements, and not the heavy ones?

@ #13 Omega Centauri
"Now, for another question, why did we end up with mostly Hydrogen some Helium and tiny amounts of Be,Li, but not mostly Iron-Nickel? "

Here ya go:
http://scienceblogs.com/startswithabang/2013/07/05/why-did-the-universe…

I assume the “surface” we are seeing in the CMB, is like the surface of a very tenuous fog, some of the photons will be older ones,</blockquote

There'll be some of that too, but that's not really the effect. Remember, looking radially out of space is looking back in time.

Some photons won't have taken the straightest line.

Some will have detoured. Some will have been intercepted then reradiated on the way. Most of those won't have reached us, though. Unless it was not a large effect.

@Denier #2 and #4: Your question here is a good one, and the point is actually quite subtle. Let's simplify to having recombination (and the CMB) happening all at once (i.e., no patchiness or ~100 kyr time duration); the analysis is the same and leads to what Ethan described in his post.

Now, keep in mind that the Universe is a three-dimensional space which is _all_ expanding. Recombination happened at BB+380 kyr throughout that whole 3D space, leading to everywhere being filled with CMB at the recombination temperature (~3000 K), with small temperature fluctuations throughout.

An observer at point 'A' looking around in all directions would see their sky as an _apparent_ sphere at 3000 K, with all of those fluctuations projected onto it.

A different observer, at point 'B', would see _their_ sky as a 3000K apparent sphere, with the same 3D distribution of fluctuations projected onto it. But now, since 'B' is a different point than 'A', that _projection_ will look different to them. That is, if a hot spot was projected to point (50,80) on the sky for 'A', it might be projected to point (72,-15) for 'B'.

Ethan's example with "our dinosaur observers" corresponds to an observation different in _time_ (meaning a slightly hotter appearing CMB) as well as different in _space_ (since the Sun would have been at a very different place in its orbit around the galaxy, and the galaxy would have been in a different location due to its motion with the local group).

Michael Kelsey,
You wrote “Now, keep in mind that the Universe is a three-dimensional space which is _all_ expanding.”

What was the Universe expanding INTO?

“But now, since ‘B’ is a different point than ‘A’, that _projection_ will look different to them. That is, if a hot spot was projected to point (50,80) on the sky for ‘A’, it might be projected to point (72,-15) for ‘B’.”

Doesn’t this violate the BB principal of isotropy?

@See Noevo #17: "What was the Universe expanding INTO?" Nothing. Which you would know if you actually studied the science involved, instead of guessing. The scale factor of space itself is changing, which uniformly increases (as a function of time) the separation between points in space, and consequently the separation between non-gravitationally-bound objects in that space.

Regarding the differing appearance of the CMB fluctuations as a function of position, you asked, "Doesn’t this violate the BB principal [sic] of isotropy?" No, it does not. Which you would know if you actually studied the science involved, instead of guessing. The FLRW metric assumes LARGE SCALE homogeneity and isotropy, and says nothing whatsoever about small scales. Your own existence does not violate the principle of large scale isotropy. The CMB fluctuations are small; they are _distributed_ in a random, statistically uniform way throughout space. When that randomness is projected onto the spherical surface of an observer's sky, it will still be uniform and random, but the detailed projected location of each fluctuation will be different for different observers.

@ WOW #9,10,11 ...
Agreed - I had forgotten the basics of photons passing through a different medium; my bad.
I took your words @7 as a litteral & responded to the case where there is no light present whatsoever to an observer.

@Michael Kelsey #16

I think I understand, but it requires the patchiness and ~100 kyr time duration. Correct me if I am wrong, but without that the CMB is effectively the 2 dimensional surface of a sphere.

If you were inside a birthday balloon, it wouldn't matter where you were. You'd still see the identical pattern on the inside walls of the balloon. It might be rotated or have aspects scaled differently depending on what wall of the balloon you were close to, but the pattern is identical.

Adding in the patchiness and ~100 kyr time duration gives the CMB depth. Then it would look different depending on your point of view. However if we had the images from the dinosaur's telescope and ours, we could create a 3D model of the CMB that would not change.

Is that correct or am I still missing pieces?

"Correct me if I am wrong, but without that the CMB is effectively the 2 dimensional surface of a sphere."

"Effectively" is not "Absolutely". It just means there's not a lot of difference in shape.

Therefore your "problem" is, yet again, your fault.

"I took your words @7 as a litteral & responded to the case where there is no light present whatsoever to an observer."

Nah, colloquial sense in the conversation that was about the light from an LCD screen TV style thingy.

Precision requires many more words and is usually not available with any words in any used language, so imprecision is inevitable.

It's one reason why pedantry should be left on the back burner. Make someone *more* correct, by all means, but check you're going to be more correct yourself first :-)

"“Doesn’t this violate the BB principal [sic] of isotropy?” No, it does not"

Added that the isotropy isn't PERFECT isotropy, just a lot more isotropy than expected to get the current conglomeration of matter, for which inflation is inferred as existing.

So See Nowt is

a) pretending that it's something it isn't
b) pretending that it not being that thing it isn't is a problem in it being what it is

Or, in other words, circle-jerk unreasoning. Necessary for a fundie moron like SN.

Michael Kelsey,
Thanks for pointing out my misspelling of principle.

I’ll return the favor and correct you: My questions were questions, not “guessing”. Note the “?”s.

Also, you say “The FLRW metric assumes LARGE SCALE homogeneity and isotropy, and says nothing whatsoever about small scales.”

Does a structure that takes 4 billion light years to cross qualify as a sufficiently LARGE clump to be problematic for such LARGE scale homogeneity and isotropy? This PhD seems to thinks so:
“The team, led by Dr Roger Clowes from UCLan's Jeremiah Horrocks Institute, has identified the LQG which is so significant in size it also challenges the Cosmological Principle: the assumption that the universe, when viewed at a sufficiently large scale, looks the same no matter where you are observing it from.”
http://www.sciencedaily.com/releases/2013/01/130111092539.htm

@Denier #20: You're still missing it. Even if the CMB happened _instantaneously_ everywhere, it would still not be the "surface of a balloon." The radiation and the temperature fluctuations (which were a consequence of underlying density fluctuations) filled all of 3D space at that time. That 3D space continued to expand and cool. An observer somewhere in that space _projects_ the distribution onto the surface of a fake sphere (the "dome of the sky" in some folks' favorite tall tale).

Different observers in different places and times will see different projections. Just as if you stand at home plate in a baseball stadium, the panoramic picture you could take would look different from the panorama taken by someone up in the cheap seats. Even though it's the same stadium.

Finally, you wrote, "However if we had the images from the dinosaur’s telescope and ours, we could create a 3D model of the CMB that would not change." This is, in essence, correct. If we had the projections from multiple, widely separated observers, then we could reconstruct the whole 3D distribution, via an effectively "stereoscopic" analysis.

Regarding the question of dinosaurs seeing a different CMB: My take is that the surface of last scattering is a 'moving target'. The co-moving co-ordinates in space, from where the CMB originates for the dinosaurs, are different to the co-moving cordinates for us. So that if we imaged the CMB over time it would give us a spherical projection of the universe at t=380,000 years, expanding through three dimensions of space, centred on the region where our galaxy originated. The dinsoaurs see a different 3d region than do we, because the CMB sphere has expanded through space in the time elapsed since then. I think this was the author's main point?

It's interesting too, to think about where the CMBR that we observe today came from. We observe that the photons were emitted about 13.8 billion years ago, suggesting a region of space 13.8 billion light-years away. But we live in an expanding universe.
According to calculations, the co-moving distance to this region of space is 45.7 billiion light years, because the universe has been expanding all the while the photons have been travelling to our telescopes.
WMAP gives the redshift of the photons as z=1091. The scale factor at the time the light was originally emitted is given by the equation: a(t)=1/1=z. So if the matter which emitted the oldest CMBR photons has a distance of 45.7 billion light years today, then at the tine of emission the distance would have been only about 41.8 million light years away. In other words, the universe has expanded roughly a thousandfold since photon decoupling.

'at the time of emission' not the 'tine' - my bad

Abstract of intro lecture or blog from any cosmologist: "The universe is INCREDIBLY uniform, and that leads to many interesting conclusions. The universe is NOT uniform, and that leads to many interesting conclusions."

I asked in an 'Ask Ethan' link about how likely we are to even notice changes -- how good our coverage is.
Here's a tool that might be applicable:
http://grail.cs.washington.edu/projects/timelapse/

@29:

Abstract of intro lecture or blog from any cosmologist: “The universe is INCREDIBLY uniform, and that leads to many interesting conclusions. The universe is NOT uniform, and that leads to many interesting conclusions.”

Heh. Yep, but understanding what they're saying in both cases is the answer to @24 and @17's question. The CMB is not a "wall" or "surface." It isn't something that exists somewhere out in space and we have to point a telescope at it to find. What it is, is a whole lot of photons flying around the universe everywhere, going in every direction. All these photons have an energy of about 2.725K +/- 0.0005K. That's the energy variance in quantitative numbers. Whether you choose to call that incredibly homogenous, homogenous, or heterogeneous really depends on the context of the conversation. Can you see the differences with a basic antenna? No, its too homogenous. What about compared to a variance of one part per billion? Well in that case, its much more heterogeneous than that.

@Michael Kelsey #25

Is there a direct correlation between the underlying density fluctuations and the time the associated area became transparent? In other words, are the photons from the relatively more dense areas of a different age than the photons radiating from the areas of lesser density?

@Denier #32: The temperature variations correspond to density variations in the early Universe. Higher density results in slightly cooler CMB (the "blue" splotches in typical maps) while lower density results in slightly warmer CMB (the "red" splotches).

They do correspond roughly to earlier vs. later times respectively, but that time variation is well within the already understood time span of about 100 kyr it took for the cosmic recombination to finish. This time interval is MUCH MUCH MUCH shorter than we can resolve with redshifts and is of no cosmological significance.

@Michael Kelsey #33

So the difference between the CMB image from the dinosaur telescope and our CMB image is roughly analogous to the constellation differences in our nighttime sky versus what constellations would appear in the nightime sky of another world located in a different arm of the Milky Way Galaxy.

The stars and voids are in exactly the same position, and we could pinpoint stars/voids in x-y-z space if we had two well spaced points of observation, but patterns that appear on each world's nighttime celestial dome is different owing to their different point of view of the exact same thing.

The CMB map we have is spheroid, not spherical. The distance between us and the "surface" of the most distant point we can image using photons correlates with temperature of the photons, but the temperature variance is not due to a difference in exposure to varying amounts of cosmological expansion redshift. Instead, the CMB temperature variance is due to the variance of gravitational redshift from areas of relative higher density versus areas of lower density.

Am I correctly understanding what you are saying?

I'm trying to understand CMB with the following very simplified model:
- at t=0 the whole universe becomes transparent
- no inflation of space, no movement of observer, no bending of light through gravity, ...
Then let's consider a set of concentric spheres S1, S2, ..., centered at the observer at t=0, with radii R1= 1 light-second, R2= 2 light-seconds. etc. So each sphere is a 2D slice of the 3D universe at t=0; each such surface cuts through very slight variations of density.
At t=0, the observer sees the temperature of the local point (just like before).
A t=1s, the observer sees R1. At t=2s, R2, etc.
Since the photons that meet the eye of the observer at time t were all generated at time 0, these photons come from a spheric surface, namely S_t.

Now we can de-simplify the model. If 10 light-second away from the observer at t=0 in some direction there's a small blob
of matter 1 light-second deep that needs 2 more seconds to become transparent, then S1 through S10 are unchanged, but after that the spheres are actually dented since for 2 seconds the light cannot have come through said blob of matter, so the observer sees the surface of the blob in that direction for these 2 seconds (S11-S12), after which progress resumes through the blob that's becom transparent, that's S12-S13. After that the observer gets to see what was on the other side of the blob; hower some light emitted was lost as it hit the blob before it got transparent, so there's a 2 second "dark cone" behind the blob that the observer never got to see: right after the "dented spheres" S11-S13, S14 is suddenly back to a normal "spheric sphere".

Thus if I'm not mistaken the CMB we see at any given time is a close-to-spheric slice of the universe when it became transparent. If we could have recorded it since that time we'd have a kind of 3D CT scan of the universe at that moment.
Since we couldn't we just get to see a spheric slice. As times flows that sphere gets bigger --- or rather, we get to see what was further at that time. More precisely, the surface advances slower when it gets into parts of the universe that got transparent later, thus it "dents in", then it suddendly jumps back to a more spheric shape whenever it has finished scanning one of those slower regions. It's not really important since it's just an error margin of 100k light-years while the base sphere has radius, er..., that's more than 10G light-years PLUS inflation right? How much is that?

It would be great to get the record of the CMB for millions of years so let's just ask that next time we get an alien visit.

@ Denier #34 : "analogous to the constellations" and "the stars and voids are in exactly the same position" ...
I see this differently. Because the dinosaurs are in our past (say 100 million years ago) they saw CMB photons that were emitted from an entirely different region of space, that is to say a region roughly 100 million lightyears nearer the Milky Way than we observe with our CMB measurements today. To use your analogy I would say the dinosaurs observed "different constellations altogether", and they saw "completely different stars and completely different voids" to those we see today, rather than seeing the same constellations, stars and voids but from a different angle or position.
However, I think when speaking cosmologically it could be that it is more convenient to take the position of our entire galaxy as essentially the same point or event in spacetime in relation to other entire galaxies (other points or events in spacetime), since the motions of stars and constellations *within* the Milky Way or any other galaxy are insignificant on cosmological scales.
Although the dinosaurs saw CMB photons from a different region of space, the saw them from the same period of time t=380,000 years.

@Denier #34: By George, I think you've got it! Yes, the CMB fluctuation pattern we see is exactly like the constellations -- a 3D distribution projected onto the 2D sky. Someone somewhere else would see a different projection, even though the actual stars are in fixed 3D locations.

@Steve #36: What you say is also true, to some extent. The full 3D pattern of fluctuations was "frozen in" at recombination, and is essentially fixed. I want to think about what you wrote to be sure, but I believe your analysis is correct.

Denier in #34 was using the "different constellations" as analogy, to help him/her picture the effect I had been trying to describe. You're quite right that for the CMB itself, the whole galaxy is tiny on a cosmological scale, so I suspect that nearby observers would see the same uK-scale pattern that we do.

@Denier, Jean-Marc, Steve, etc. Thank you all for a very interesting and productive discussion! It's always a pleasure to participate in an occasion where somebody learns something they didn't know before. That whole "scales falling from the eyes" and whatnot... :-)

@ MK #37
"even though the actual stars are in fixed 3D locations."

How doe this work when there is precession of the stars; and, when our future is going to be toppled with Andromeda intermingling? Nothing will remain 'fixed', surely.

By the by, how do you pop those smilies in?

@PJ #39: The secret to doing good physics is know which approximations are valid, and when. The problem as posed was discussing the effect of projecting a 3D distribution onto a 2D "sky" for widely separated observers. The obvious approximation is to keep the 3D distribution fixed, and to ask what the different observers would see under those conditions.

If you relax that approximation, for the case of stellar constellations, then obviously different observers separated in time at the same location will see different things, since we know the stars move.

Apparently, the discussion-board software here is able to identify and replace text-based smilies with icons ("emojis"?). I typed ':', '-', ')', and it got posted as the yellow happy-face icon. Here, I'm attempting a "winky" (using a semicolon) ;-) , and here a "smirk" (using a slash) :-/ .

Thanks, Michael. And 'ahah' to para 3.

@ Michael Kelsey#38

Thank you so much for your effort in answering questions and patience when I frequently go off the rails. I really appreciate it.

@ Ethan

I also want to thank you for putting in the work you do on this site. Without it, I wouldn't even know what to ask.

@Denier #42: You are most welcome!

There is a clear difference between an interested layman and a crackpot, both of which may start out with quite "unconventional" *cough* views of science/physics: The former is interested in learning, and is likely to change their views with exposure; the latter is steadfast in their knowledge, and certain that anything opposing it is part of a vast conspiracy to "deny the truth."

It's been bugging me that I didn't get all of it correct because I took the universe expansion effet in the wrong way, so I read a bit of wikipedia about CMB, and it says :
we see the points that emitted their light about 13.7 Gy ago. Those points are today at a distance of 43G light-years (because the universe has inflated meanwhile).
However I find it more meaningful to reason in terms of the ghost universe that we still get to see thanks so the CMB, and inflation actually corresponds to a _slower_ speed of light as times passes: rapidly slowing at first since the Universe was quickly expanding, and not slowing much lately since the Universe is expanding much more slowly. So the virtual CMB sphere that was seen right after recombination was first expanding at v=c, then slower and slower, and now it is something like v=c/z with z=1100 but I'm out of my depth here so I'm not claiming anything. Whatever the case, the sphere we see today had radius (again, in the ghost universe of recombination time) only 40 M ly according to wikipedia; and it will take many years (perhaps 1100 years) for us to see just 1 ly further of this ghost universe image. Well, except for the bumping back effect behind late regions.
But we don't get an a mathematical slice of the ghost image, there's some depth effect involved, because at any given point recombination took some time to take place, which means that at first just a few lucky photons could avoid being scattered again before coming to my eye (those come from further away), then more and more got their freedom, until finally the last unlucky ones had their final interaction (those come from closer when they reach me). This recombination time is estimated at 50 ky by wikipedia. So there are two types of effects that deviate from the mathematical sphere:
- denting, because some regions underwent recombination later than others. Is that also a 50 000 years effect? If so it's 0.125% of the 40Mly radius, and it turns out the sphere is only spheric to that degree after all.
- depth, because at any given point recombination was not instantaneous, so we see an average of a 50 kly deep region of the universe (with more weight in the central region)
Note: if recombination time was really 50 ky the depth to take into account is actually lower than 50 kly since (virtual) light was slowing down quicky, and this depth depends on the time when recombination starts (shorter in late regions) but I'm not getting into this.

So how much time do we have to wait before we get to see an entirely new slice of the ghost universe? Meaning there's no more overlapping of these 50kly deep slices? Well that's 50 ky times slowing factor. If my lucky guess of 1100 is correct that's 55 My --- dinosaurs went extinct 66 My ago, so we do see an entirely different CMB than the dinosaurs --- probably with some correlations though.
This seems to tell that CMB changes only very slowly with time. Each point of it corresponds to a very wide (40 Mly x 2pi / resolution) but rather thin (50 kly) region of the ghost universe.

Now I'm confused about the following things :
- does CMB tell that there's some absolute reference system of time and speed in our universe? Look at CMB -> compute the mean redshift value -> deduce observer current time ; CMB -> compute the doppler effect that would normalize the image (uniform local mean temperature) -> deduce observer absolute speed
- Ethan says "We actually have sufficient evidence that the CMB’s temperature was hotter in the past; as we look to higher and higher redshifts, we see exactly this effect." but how can someone see the CMB at various redshifts?
Looks like I got it all wrong :-/

@Michael you're welcome :)
I don't understand your usage of the word "projection" since this refers to a 3D to 2D reduction process while we see an expanding spheric 2D slice of a fixed 3D universe.
I'm picturing a really big swiss cheese that's being eaten by a lot of mice and I'm floating in the center of the big cavity they've dug over time so I can see where the tiny holes in the cheese are on the surface of that cavity, and if I wait a few millions years the mice will have eaten a bit further and I'll see new holes haha :)

@Jean-Marc #44: Towards the end of your comment, you ask, "[D]oes CMB tell that there’s some absolute reference system of time and speed in our universe?"

No, it doesn't. The CMB provides a _particular_ reference frame that all observers can agree upon. But it is not an "absolute" frame in the Newtonian sense, just a wonderfully convenient one.

As you describe, any observer anywhere can measure their own motion with respect to the CMB (the dipole anisotropy), with confidence that the CMB will look the same to any other observer.

The use of pulsar timing arrays to observe gravitational waves
is similar. Separated observers can use the same set of pulsars to define a common coordinate system.

But that doesn't mean the CMB, or the pulsar array, is an "absolute" system which violates relativity. The laws of physics are the same in the CMB frame, in a pulsar-array frame in the Milky Way, or in the rest frame of the Milky Way as it flashes through space toward the Great Attractor.

@ Jean-Marc #44
A few things occurred to me reading your post. Inflation happened at t=10^-36 seconds to t=10^-32 seconds, when the universe inflated by a factor of around 10^26 in far less than a trillionth of a second. So I'm not sure inflation is specifically relevant to consideration of photon decoupling at t=380,000 years.
What is relevant is that cosmologists tell us the tiny inhomgoneneities we observe in the CMB are due to quantum fluctuations in spacetime that were writ large upon our universe by the end of the inflationary epoch. These fluctuations 'seeded' tiny variations in the density of the post-inflationary universe - gravity did the rest.
The expansion that *was* occurring at the time of decoupling was the same expansion our universe experiences today, driven by the intrinsic energy of spacetime known as the ‘cosmological constant’ and/or ‘dark energy’. Redshift or ‘z’ is the amount that the wavelength of observed photons has been ‘stretched’ by the expansion of the universe. The CMB photons are measured at z=1091.89 – in other words the universe has expanded a little over a thousandfold in 13.8 billion years – by comparison the inflationary epoch was startling! The expansion of the universe is also thought to be accelerating, however I’m much less well read on this acceleration and will defer to others.
I think there is value in treating the ‘surface of last scattering’ as explicitly that, a 2 dimensional surface or ‘projection’. In my reading on the subject, this is how most authors treat it - they tend to ignore its 3 dimensional 'depth'. I suppose, at the end of the day, this is how we receive the photons at our telescopes today, as a photon 'projection' of the actual universe at approximately t=380,000 years. Today a certain projection is revealed to our telescopes - in one year's time a projection will be revealed from one light-year further away in the universe. This is relevant since it is the ‘expansion’ of the 'visible universe' over time due to the finite speed of light, which is a different matter to the expansion of the 'physical universe' due to the cosmological constant/dark energy. It is still valid IMHO to consider the visible universe as being 13.8 billion ly in radius - in physics one choice of co-ordinate system is just as 'real' as another, for example the ‘co-moving’ co-ordinate system which holds the radius of the visible universe to be 45.7 billion ly.
It's interesting to remember the ‘visible universe’ is bounded by the surface of last scattering. The 'observable universe' is about 2% larger at 46.6 billion light years and may be detectable to us in the future by means of neutrino or gravity wave telescopes.
The CMB doesn't 'change' over time per se, it was a specific period in the history of the universe, that occurred everywhere in the universe at (approx) t=380,000. What changes rather is our *observation* of the CMB - we observe a different part of the CMB (due to the finite speed of light) one lightyear further away per year, in every direction in the sky.
Your swiss cheese and mice analogy sounds spot on to me - lol!

I'm also curious about the peroid following photon decoupling, which covers the epoch until the first starlight - called the 'Dark Ages'.
The NASA WMAP website says: "The expansion of the universe gradually slowed down as the matter in the universe pulled on itself via gravity. More recently, the expansion has begun to speed up again as the repulsive effects of dark energy have come to dominate the expansion of the universe."
The Dark Cosmology Centre at the Niels Bohr Institute says: "This period was dark in the sense that there were no sources of light in the Universe. Yet, it is crucial for our understanding of cosmology as this was when the first structures formed through gravitational instability, in particular the first stars, galaxies and super-massive black holes. The most intriguing questions lie at the edge of this observationally unexplored dark age."
Could be my first 'Ask Ethan"!

Hi,
Jean-Marc above has got it right about the time dilation issue above, and how long it takes before we see a new CMB.
A helpful way to see this is to consider two blobs at the "front" and "back" of the CMB scattering shell.
Let's take for example blob A at z = 999 at the "front", blob B at z = 1199 at the "back", so the delta-z is 200. These map to light setting off when the age of the universe was ~ 431 kyr from A (CMB temp then = 2725 K) and age 317 kyr from B. (CMB temp = 3278 K). To see both of those blobs "now", the light from B must have passed A exactly when the light from A we now see was emitted, so the light from B travelled the extra 114 kyr "then", and blobs A and B were ~ 114 kly apart around the midpoint at z = 1099 (not exact but close enough), and they will be 114 kly * 1100 = 125 Mly or 38 Mpc apart today ( but we will never see what they emit at their time = 13.8 Gyr ).

Note the light from B redshifted by 1000/1200 down to 2725 K when it was passing A, so all the light ends up as 2.725 K today.

Next, consider what happens to the photons emitted by blob B at the later time 431 kyr; if there were a lighthouse in blob B flashing once per sec in B frame, we would see flashes every 1200 sec now which gradually speed up to ~ 1000 sec as the redshift of B drops, so around 125 Myr in our future we will see the photons emitted when B was at 2725 K . (Our CMB temp will also have cooled to ~ 2.70 K but this is a small correction. At that point 125 Myr in our future, B will be at the front of the CMB, A will be transparent so we won't see it, and a new blob C will be at the back so we will see a basically different shell of CMB. (Today C is at z ~ 1400 but nearly all its photons get scattered).

Hope that helps, W.