"Einstein's gravitational theory, which is said to be the greatest single achievement of theoretical physics, resulted in beautiful relations connecting gravitational phenomena with the geometry of space; this was an exciting idea." -Richard P. Feynman
When Einstein's theory was first proposed as an alternative to Newtonian gravity, there were a number of subtle but important theoretical differences noted between the two. Einstein's theory predicted gravitational redshift, time delays, bending of light and more. But what was perhaps most remarkable is that unlike Newton's gravity, Einstein's general relativity predicted an entirely new phenomenon: gravitational radiation.
Image credit: Tod Strohmayer (GSFC), CXC, NASA - Illustration: Dana Berry (CXC).
Much like how charged particles moving in a magnetic field accelerate and emit radiation in the form of photons, masses moving in a gravitational field accelerate and emit radiation in the form of gravitational waves, or ripples in the fabric of space itself. Even though these waves move at c, the speed of light in a vacuum, the expanding Universe carries them even farther, as these ripples ride atop the fabric of our expanding spacetime.
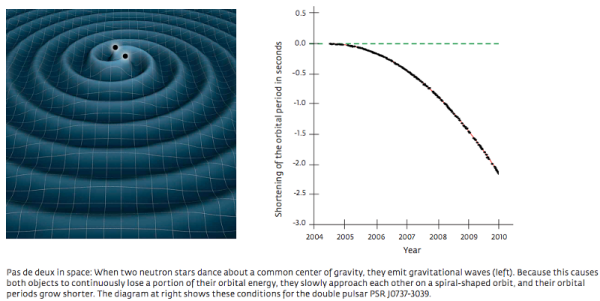Image credit: NASA (L), Max Planck Institute for Radio Astronomy / Michael Kramer, via http://www.mpg.de/7644757/W002_Physics-Astronomy_048-055.pdf.
Go read the whole story of their remarkable behavior on this week's Ask Ethan!
- Log in to post comments
More like this
Hope my 50-year-old recollection of E & M is not too dim, but I seem to recall that Maxwell's equations provided a method to calculate a value for c from physical constants which were already known. That the value thus calculated corresponded to the measured value of the speed of light was taken as evidence that light was, indeed, an electromagnetic wave. Does GR or any other gravitational theory provide a method to independently calculate the speed of gravitational waves?
Maxwell's equations show speed of electromagnetic waves is c and Einstein's equations show speed of gravitational (space-time) waves is c.
But it is still a big question why both speeds has to be equal. I think only TOE can provide the answer if found someday.