"The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality." -Hermann Minkowski
When it comes to gravity, you probably think you understand it pretty well.
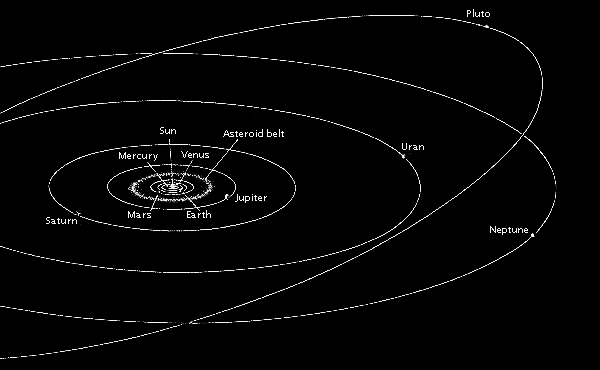 Image credit: Heavens Above, via http://heavens-above.com/.
Image credit: Heavens Above, via http://heavens-above.com/.
Everything with mass (or energy) attracts everything else with mass-or-energy, explaining everything from falling terrestrial objects to the orbits of the planets to the formation of the largest structures in the cosmos.
And yet, this picture is only an approximation of what we know to be a more fundamental truth. The idea that objects feel gravitational forces and accelerate in response to them falls well within the realm of our common experience, and it's very tempting to describe all gravitational interactions in those terms. This is what our best understanding of reality was for centuries, thanks to the work of Isaac Newton.
 Image credit: Gilkey63 of http://gilkey63.blogspot.com/.
Image credit: Gilkey63 of http://gilkey63.blogspot.com/.
But if we did that, we'd miss out on some very, very important subtleties of Einstein's relativity. In particular, the biggest revolution that came along with Einstein's work was the idea that instead of space and time being independent, fixed entities, they were actually an inseparable combination -- spacetime -- whose shape itself determines the trajectory of all objects, both massive and massless, that lie within it.
In addition, the shape (or curvature) of spacetime is determined by the presence and distribution of all the matter and energy that exist in that spacetime itself! When we have an idealized system, like a very heavy mass that's orbited at a large distance by a much smaller mass, Newton's gravity -- and Newton's picture of forces and acceleration -- are an excellent approximation.
But even excellent approximations have their limits.
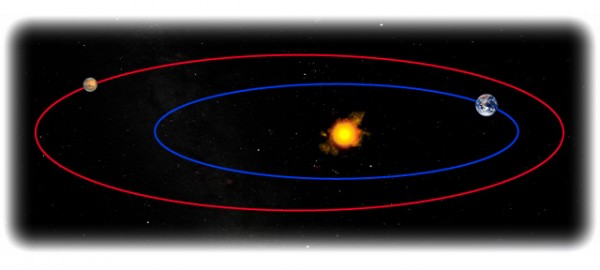 Image credit: Dave Flynn of http://www.quia.com/.
Image credit: Dave Flynn of http://www.quia.com/.
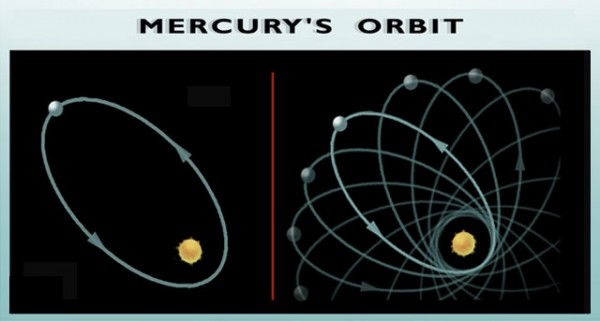
One of the remarkable conclusions you arrive at in Newtonian gravity is that any tiny mass that orbits a much larger one will revolve around it in a perfect ellipse, returning along the same exact path each and every revolution. When Kepler discovered that the planets did, in fact, make ellipses around the Sun, this was an unexplained phenomenon until Newton's law of gravity came along. But, like I said, even though it's a very good one for our Solar System, this is only an approximation.
In reality, all of the planets fail to make a closed ellipse in their orbit around the Sun, missing by just a tiny amount. Interestingly enough, the closer you are to the largest mass, the more you miss your last orbit by. This is because spacetime is actually curved more severely the closer you are to a larger mass, and where the spacetime curvature is more severe, that's where the most interesting, non-Newtonian predictions of General Relativity come into play.
 Image credit: created by Starosta, retrieved from http://www.holoscience.com/.
Image credit: created by Starosta, retrieved from http://www.holoscience.com/.
One of the more spectacular predictions of General Relativity -- in sharp contrast to Newtonian gravity -- is that not only do these orbits fail to close, but over long enough timescales, they actually decay. That's right, if you wait long enough, the planets will all eventually spiral inwards towards the center of our Solar System, where they'll be gobbled up (or, for a less scary phrasing, where they'll merge) with the mass at our center.
Don't be alarmed by this; it'll take some 10150 years for this to happen, far longer than the lifetime of any star in the Universe. But that's only because all the planets are so far away from the Sun, relative to its paltry mass. But this means if we can find a system where a mass orbits much, much closer to the dominant mass in its system, we should be able to test this relativistic prediction, and see whether, in fact, the orbit does decay, and whether it decays at the rate predicted by Einstein's theory or not.
To practically test this, a Sun-like star will simply not do, for the simple reason that it's too big! But if we had an object that was as massive as the Sun, but maybe only the physical size of a mountain, we'd be in business. Luckily for us, not only the Universe but our own galactic neighborhood is littered with these objects: neutron stars!
These objects are the leftover cores of supermassive stars that have exploded in a Type II supernova, but are not quite massive enough to collapse down into black holes. One of the most massive neutron stars known is PSR J0348+0432, which weighs in at about twice the mass of the Sun, but is only maybe 10 kilometers (6 miles) in radius. For a neutron star, it's remarkable for three reasons:
- It's a pulsar, which means that, as it rotates, it sends out radio emissions in two beams. While it's conceivable that all neutron stars are pulsars, we're fortunate enough to have one of these beams point directly at us, which is very rare. 25-times-per-second, we receive a very regular pulse from this neutron star, which is observable with a good radio telescope.
- It's in a binary system, which means that there's another mass orbiting it. This is a very special case for Einstein's relativity, as we'll not only have precessing elliptical orbits, but also orbital decay and -- if we can someday detect it -- gravitational radiation.
- And finally, that other mass is a white dwarf star, a very small object about the mass of the Sun but the physical size of Earth, that's so close to the neutron star that it completes an orbit every 2.5 hours, meaning that the entire orbit of the white dwarf around this neutron star would fit inside of our Sun!
Here's an artist's impression of what this would look like.
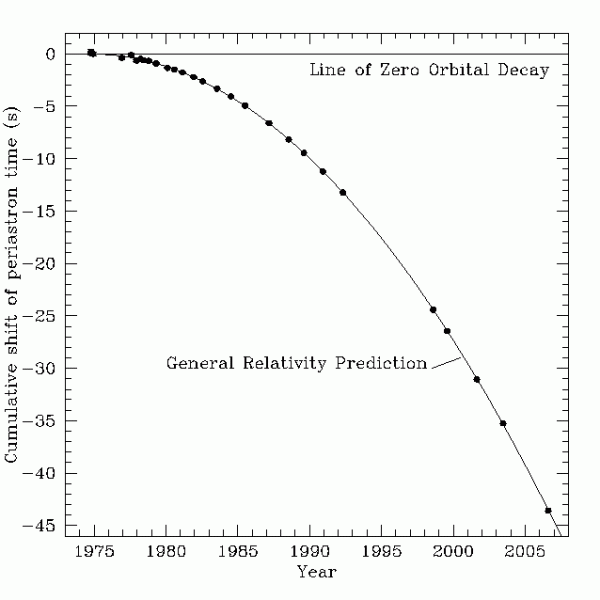
But there's never been a system found where gravitational decay was occurring this fast, or where we've been able to study spacetime that's curved this strongly. In other words, this is new territory for relativity, and one of the strongest tests ever performed! Want to know what we found?
The orbital period of the binary changes by a cumulative eight microseconds-per-year, in exact agreement with Einstein's predictions! This is really remarkable, because many of the serious competing alternatives to Einstein's relativity have much larger predictions in regions of strongly curved spacetime; this observation rules them out!
So if you've been wondering what Einstein and General Relativity have done for you lately, here's your answer: in the most extreme conditions ever tested, where the curvature of spacetime is stronger than any system we've ever tested before, General Relativity's predictions exactly matched the effects we painstakingly observed.
 Challenge Einstein at your own peril, folks, because nature -- at every turn we've been able to test -- obeys General Relativity every single time, including in this new way!
Challenge Einstein at your own peril, folks, because nature -- at every turn we've been able to test -- obeys General Relativity every single time, including in this new way!






Coincidentally, today's XKCD was on the topic of proving Einstein wrong, but about something more mundane than this.
Two masses orbiting each other change their positions all the time (both masses the same for simplicity).
Due to runtime of gravitation one of the masses "feel" the gravity of the other from an angle, which is a bit less than 90° to its own velocity direction and the "felt" distance is a bit smaller.
The mass will accelerate and lower its orbit to counterbalance.
Thus no energy is needed to be radiated from this system.
What is wrong with this idea?
thanks ethan
Ethan, did this:
http://xkcd.com/1206/
bring on the idea for this thread???
SHWAR_A, a dipole will radiate if it is made to oscillate the charge.
The masses are "charges" for gravity.
Therefore, like with electric fields, the rotating system will radiate gravity waves.
Your scenario falls down in that conservation of momentum AND energy must BOTH be conserved. Therefore the acceleration of the two objects cannot be done to the same level as to take up the energy lost to gravitational potential and the excess energy (or lost momentum) must be radiated away (or taken from a third mass) to balance the equation.
I'm kind of glad this wasn't about an experiment at LHC I just read about that's seeking to test whether antimatter experiences anti-gravity. I was kind of dumbfounded by that.... Does ANY serious theory predict that? Do ANY serious scientists expect to find it so?
Ethan
Very nice observations and explanation.
I did not know of this prediction of general relativity.
Can someone clarify, is this phenomenon related to frame dragging or something else?
Here we have a neutron star of mass N and a white dwarf of mass W that are orbiting at a radius R. Is there a simple equation (derived from general relativity with the appropriate assumptions) that gives the change of radius R as a function of
dR = f(N, W, R) dt or something like this. what is this equation?
Thanks anyone.
@ BenHead: The expected result of that experiment would be that antimatter experiences gravity like normal. There are all sorts of problems if this wasn't the case. Like, Conservation of Energy and Einstein Equivalence (inertial mass = gravitational mass) type problems.
But it's never been measured, so we don't know for sure. That's one of the things I love about science -- always seeking to verify if reality conforms to our expectations.
P.S. It's the ALPHA project that is doing the instrument, which is part of CERN but not part of the LHC.
@OKThen
you can find some of the formulas here
http://arxiv.org/abs/astro-ph/0405178
pages 16,17,18
@Wow (#5):
Thanks.
Does this mean that accelerating a mass, like shooting a bullet to a metal target, will generate gravitational waves? Both times, at firing and hitting moment?
I do not understand, why there is "excess energy" and why "acceleration [...] cannot be done to the same level". I have calculated the scenario and found that the part of transformed energy is complete: the result contains the exact formula for gravitational redshift. Could you please explain a bit more specific (perhaps with formulae)? Thanks a lot in advance.
So when the White dwarf will 'merge' with the Neutron Star, it should result in a type IIA supernova.
And if we can predict this decay, we should be able to predict the time of the supernova.. Hmm not sure if my thoughts are true
As much as you get an antenna from sending electrons once down a line and then stopping.
I.e. naff all to consider.
The "Excess energy" is that the rotational momentum goes as velocity times radius of motion, and kinetic energy goes as velocity squared. Therefore it isn't possible to conserve both at the same time without either gaining momentum or losing energy when lowering to a different orbit.
It doesn't have anything to do with gravitational redshift (at least as far as I'm aware). Just the two classical mechanical equations for rotational momentum and kinetic energy. One has a v in there once, the other has a v in there twice.
@Wow (#13):
OK, I assume we could never detect gravitational effects generated by home-made acceleration.
In our binary system above, if energy stays constant, the rotational momentum of the decaying orbit decreases, but the spins of both masses increase by the same factor. Rotational momentum is transported within the system.
Assuming both masses always face the same side to each other: while their orbit decays they both gain exactly that amount of rotational momentum needed to maintain this feature.
Following this the complete system conserves energy _and_ rotational momentum.
What do you think?
@ SCHWAR_A:
We can easily rule that scenario out by virtue of this being a pulsar with a rotational period of 40 ms, but an orbital period of 2.5 hrs.
I'm not sure it'd work out that the increase in rotational angular energy would match the decrease in orbital angular energy -- the size of the moment of inertia for the orbital energy seems like it would just be too much higher. But I'd have to do the math and I have other math I should be doing. >_<
But it doesn't obey at the nano scale. But for everything else E's your man.
Anyway, I think it has the exact same problem -- the inertia goes up or down as w, and the energy as w^2
That's where you have your problem.
The energy cannot stay constant within the binary system AND get closer together.
The "if" doesn't happen.
Might as well say "If the Flying Spaghetti Monster can travel faster than light, then it can make changes before its presence can be seen!".
@Wow (#5):
"The masses are “charges” for gravity. Therefore, like with electric fields, the rotating system will radiate gravity waves."
The big difference is that the electron's spin can't change and thus "needs" to radiate away the excess energy.
With gravitational "charges" this is different. Their parts all have their own gravitational reaction to their specific positions within the current field.
@CB (#15):
Think about convections within stars: how would they look like if there would not be this feature that all atoms gain the rotational momentum during descent?
If you sit on a slowly rotating turntable with a globe in your outstretched hand: if the globe does not rotate relative to you, it will also not start rotating if you pull it towards you. This is known as spin-orbit-interaction...
The spin of an electron has no relevance here, Schwar.
None.
Not a sausage.
Bugger all.
In convection the falling material does so because it is losing energy. It then rises again after gaining energy from the hotter interior of the star. That's the whole point of convection.
@CB (#15):
"...I’m not sure it’d work out ... But I’d have to do the math and I have other math I should be doing."
OK, here is the math:
We start with
G·M·m/r = m·v² = m·ω²·r² = ω·L_orb
where m is the mass orbiting around M with distance r, speed v, angular velocity ω and rotational momentum L_orb.
Now we decrease the distance a bit by the factor
1 - Δr/r
Therefore the speed increases with
(1 + Δv/v)² = 1 / (1 - Δr/r)
The angular velocity is affected by
(1 + Δω/ω)² = (1 + Δv/v)² / (1 - Δr/r)² = 1 / (1 - Δr/r)³
which is KEPLER's 3rd law.
The rotational momentum of the orbit finally changes with
1 - ΔL_orb/L_orb = (1 + Δv/v)² / (1 + Δω/ω) =
= √(1 - Δr/r)³ / (1 - Δr/r) = √(1 - Δr/r)
This is the excess, which must be counterbalanced by the spin of m for conservation.
We assume "face-to-face" spinning of m, i.e. one turn of spin per turn of orbit:
ω_spin = ω_orb = ω
The rotational momenta are
L_orb = m·ω·r²
and
L_spin = m·ω·R²
with R some constant radius of m related to its rotational momentum.
We eliminate ω and get
L_spin = R²/r² · L_orb
Changing L_spin means increasing its angular velocity by (1 + Δω_spin/ω),
changing L_orb means decreasing its angular velocity by (1 - Δω_orb/ω) due to
L_spin·(1 - ΔL_spin/L_spin) = R²/r² · L_orb · √(1 - Δr/r) / (1 - Δr/r)² =
= R²/r² · L_orb·(1 + Δω_orb/ω)
and with the changes extracted
ΔL_spin = R²/r² · L_orb · Δω_orb/ω
which is
m·Δω_spin·R² = R²/r² · m·Δω_orb·r²
and thus
Δω_spin = Δω_orb
The increase in rotational angular energy (spin) matches the decrease in orbital angular energy.
Q.E.D.
"This is the excess, which must be counterbalanced by the spin of m for conservation."
And this is moved across HOW?
Look up why, despite an axial rotation being possible for a diatomic molecule, there is no rotational state for the diatom along its longitudinal axis: no asymetry to measure the rotation with == no axial rotation.
@Wow (#23):
"And this is moved across HOW?"
Please look at my post #2.
Those parts of m, which are farther away from M "feel" an angle that is a little bit smaller than the angle of those parts nearer to M. This effect causes an acceleration of m's spin at the same time as m's orbit decays.
"...diatomic molecule..."
As far as I know these are more alike gyroscopes circling around their long axis and thus react with inertia to changes of current rotations. You may watch typical turntable experiments with a handled gyroscope.
By the way, what is the rotational momentum of such molecule? I assume ħ/2 and thus could not handle changes in angular momentum. Is this correct?
This assumption is emprically false. See again see CB @15.
So what you have done here is - at best - shown that for one special, theoretical type of two-body case, (spin+orbital angular energy) is conserved. But that does not prove that that quantity is always conserved as a general rule, and your case doesn't seem to apply to the system given in the post. Or any other real world system I can think of, with the possible exception of a geosynchonous satellite always facing down/inwards.
SCHWAR_A, I do believe you made a math error somewhere. My forum-fu is weak, so forgive the bad formatting. For starters, I'm using u for mu and w for omega. Let:
r = initial orbital radius
f = ratio of new orbital radius to initial.
R = planetary radius.
u = G(M+m) = (w^2)(r^3)
w0 = initial angular velocity = (u/r^3)^(1/2)
L_r0 = initial oRbital angular momentum = w0 * r^2
L_s0 = initial planetary "spin" angular momentum = w0 * R^2 = (R^2 / r^2) * L_r0
w1 = final ang. v. = (u/(fr)^3)^(1/2) = f^(-3/2) * (u/r^3)^(1/2) = f^(-3/2) * w0
L_r1 = final orbital ang. m. = w1 * (fr)^2 = f^(-3/2)*w0 * (fr)^2 = f^(1/2) * r^2*w0 = f^(1/2) * L_r0
L_s1 = final planet ang. m. = w1 * R^2 = f^(-3/2)*w0 * R^2 = f^(-3/2)*L_s0 = f^(-3/2) * (R^2 / r^2) * L_r0
L_s1 = f^(-3/2) * (R^2 / r^2) * L_r0
Your supposition is that momentum is conserved between the initial and final states, as in:
L_r0 + L_s0 = L_r1 + L_s1
L_s0 = (R^2 / r^2) * L_r0
L_r1 = f^(1/2) * L_r0
L_s1 = f^(-3/2) * (R^2 / r^2) * L_r0
L_r0 + (R^2 /r ^2) * L_r0 = f^(1/2) * L_r0 + f^(-3/2) * (R^2 / r^2) * L_r0
1 + (R^2 / r^2) = f^(1/2) + f^(-3/2) * (R^2 / r^2)
This equation has at most two real roots, one of which is 1.
Momentum is not conserved when changing orbits and maintaining tidal lock.
If forgot a factor of "m" in all the angular momentum equations, and similarly w*R^2 assumes a spherical shell. Doesn't change anything; the m would just get divided out, and (R^2/r^2) would just become some other constant.
Now what if you allowed the planet to get out of tidal lock as the orbital radius reduced? After all, if you did the math on the gravitational force that you believe produces the torque to speed up the planet's rotation as it spirals inward, it might end up that it accelerates it faster than necessary to keep tidal lock.
The problem then is that by matching the momentum by changing the angular velocity, you will not be able to match the energy because of the square factor.
Either energy or momentum must change in the orbital system -- GR predicts that energy would be emitted, solving the conundrum.
my_last_post =~ s/Spherical shell/ring/;
"By the way, what is the rotational momentum of such molecule? I assume ħ/2 and thus could not handle changes in angular momentum. Is this correct?"
You're talking about rotation around the normal axis to the long axis.
I'm not talking about that.
I'm talking about the rotation AROUND THE LONG AXIS, not the axis at right angles to that.
@eric (#25):
You may vary R as you like in my above calculation to achieve any ratio between ω_orb and ω_spin. R doesn't matter for the principle: Δω_spin = Δω_orb. Therefore my calculation is not just a specific case. This case is just more easy to understand.
@CB (#26):
It is quite easy: write the special characters in a word document and just copy and paste them. Or, copy and paste from this list:
º¹²³ªⁿ‾
½ ¼¾ ⅛⅜⅝⅞
αßγδεθλνπρστφψω
ΓΔΣΛΚΦ
·٭*∞√∫±≈≠≤≥≡→↑←↓
∂ℓ℮ħ
I have put it into a text-document and copy from it...
You can't vary R as you want. You have to solve all equations at the same time if you don't want radiation of energy via gravity waves to happen.
Varying R (or really, what we should just be using, the moment of inertia of the planet about its rotational axis) doesn't change the ratio of the angular velocities by itself. Because in general there is no relationship between orbital angular velocity and rotational angular velocity, so these would just be two independent measured values. The only reason there was a relationship was because you proposed one of the special cases where there is.
Schwar: your "R" is the radius of your object ("with R some constant radius of m"), it can't vary at all unless your object is deforming or losing mass. If either of those things are happening, then rotational energy is not all going to spin (or vice versa), and you're still wrong.
But I think you are still missing the conceptual point. You cannot assume face to face spinning of the two bodies, because that isn't what is actually happening. To the extent that your model depends on that assumption to work, it is not describing any real phenomena.
Thanks to all.
I unfortunately wrote "with R some constant radius of m". R is constant, but not really the radius, which is the boundary of visible matter. R is just a parameter describing the spinning mass of m: L = m·ω·R².
Instead I should better have written L = m·ω_spin·x·R_m² with x the ratio of ω and ω_spin. With this in my calculations is R² = x·R_m² constant. Both Δω are affected by this ratio in the same way. Thus the increase of the angular velocities are the same. If for example m spins with 2ω and orbits around M with ω, its spin increases to 2ω+Δω and its orbit to ω+Δω.
And yes, I can see that the sum of rotational momentum seems not conserved. Thus my supposition from #14 "Following this the complete system conserves energy _and_ rotational momentum" must be denied so far.
Again thanks a lot for this discussion.
I scrutinized the excess of rotational momentum from CB's calculation L_s1: it is exactly related to the increase of the kinetic energy of the spinning m.
With this we would have an energy transfer from orbit decay into increasing kinetic energy of m's spinning...
With no mechanism that would let that happen...
But it still doesn't work! You can't conserve both energy and momentum. Let's start with the same scenario, a planet tidally locked to the star it orbits. But let's let the final angular velocity of the planet vary as necessary to conserve momentum. Let:
q = ratio of initial orbital moment of inertia to moment of inertia of the planet about its rotational axis. This replaces (R^2/r^2) in my previous equations.
s = ratio of initial planetary angular velocity (=ω0) to the final angular velocity of the planet's rotation.
L_s1 = s*L_s0 = s*q*L_r0
So going back to my penultimate equation but changing the value of L_s1, we have:
L_r0 + q*L_r0 = f^(1/2)*L_r0 + s*q*L_r0
Solving for s to see what is needed to preserve momentum:
s = (1 + q - f^(1/2)) / q
Now let's look at conservation of energy:
ω0*L_r0 + ω0*L_s0 = ω1*L_r1 + s*ω0 * L_s1
ω0*L_r0 + ω0*q*L_r0 = (ω0*f^(-3/2))*(f^(1/2)*L_r0) + s*ω0*s*q*L_r0
ω0*L_r0 + ω0*q*L_r0 = ω0*f^(-1)*L_r0 + s^(2)*ω0*q*L_r0
divide by ω0*L_r0:
1 + q = (1/f) + q*s ^2
s = √( (1 + q - (1/f)) / q)
√( (1 + q - (1/f)) / q) = (1 + q - f^(1/2)) / q
Guess when this equation holds true? Go on, guess. That's right! When f =1! And therefore s is also 1! Only when nothing changes are both energy and momentum conserved.
This is why the Conservation Laws are so powerful. Having to obey both Conservation of Energy and Conservation of Momentum constrains possible scenarios greatly. Just by doing this math I can show that it is impossible for an orbit to decay by any mechanism unless that mechanism causes the system to lose energy somehow.
Friction (or collisions in general) are one such mechanism. Energy is transferred to the objects collided with, allowing orbital decay. In the absence of that, however, we should never see an orbit decay. Unless, of course, there are gravity waves.
@CB:
OK so far: in our system both energies increase when momentum is conserved. This excess has to be radiated away.
I just noticed that we never considered both masses in the system, m and M. Mustn't we handle both the same, but contrary balanced?
I.e. E_M = E_m and L_M = L_m, which means in our binary system:
E_m - E_M = 0
L_m - L_M = 0
which is valid all the time...
What do you think?
You can simplify by changing to the CoM of one of the bodies. No need to work from an inertial frame where BOTH bodies masses are moving.
@Wow:
OK, but then we would never apply forces to M itself. But it is part of the system, isn't it? M has its own orbit around the barycenter and its own rotational momentum, both influenced by m.
Thus I think we cannot just reduce M to a point in the barycenter with no other attribute than having a mass.
M and m have to balance: actio = reactio.
If we would like to detect gravitational waves we are in line with the frame of the barycenter, not in that of M. In the frame of the barycenter everything is balanced.
Any idea?
"Thus I think we cannot just reduce M to a point in the barycenter with no other attribute than having a mass."
guess that's why it's called an approximation
And the error of that approximation depends on any dipole moment of the individual mass.
For dense heavy stars like white dwarfs and neutron stars, that's so close to zero as to make no odds for any calculation necessary. The density makes any deviation at the macro scale from a perfect sphere so energetically precluded as to be impossible to maintain.
What "approximation" do you mean?
Both masses of PSR J0348+0432 are about the same (~2x and ~1x solar mass) and their barycenter is far outside both bodies somewhere between (~550000 km / ~280000 km).
Just looking at the runtimes we find factor ~3 related to a system with an adjusted mass placed at the barycenter instead.
meaning one object is much much smaller than the first. thus it's approximated to a point mass.
@Sinisa Lazarek:
...then you didn't get my idea, sorry.
The basic idea is that gravity needs time and while in our binary system the sending M is moving, the receiving m is moving also, which will reduce the "felt" distance of one mass to the other. This small delta in distance causes acceleration. This principle shall be valid for both bodies.
In this scenario the expansion of any body doesn't matter, only their distance and orbital speeds are of interrest.
But I don't understand why all of this is dealing with orbit's and Kepler etc.. when it's not about that. It's about relativity.
The fact that you have 2 pretty significant masses (solar mass) orbiting one another at huge speeds and small distance, means you're dealing with space curvatures and high energies. It's not about Kepler, it's about Einstein. Since they both have similar mass, means they curve spacetime to a similar degree, just one is much smaller and orbits.. as it curves space-time is "drags" it, sending ripples through spacetime. That's the energy that's being lost, and that's what causes the orbit to decay.
for IMO good explanation check wiki article on grav. waves, subsection "Power radiated by orbiting bodies"
http://en.wikipedia.org/wiki/Gravitational_waves
@ SCHWAR_A
"I just noticed that we never considered both masses in the system, m and M. Mustn’t we handle both the same, but contrary balanced?
What do you think?"
I think you'd have the SAME DANG PROBLEM. You'll have four equations with four variables, the two orbit ratios and the two spin ratios, and once you solve you'll find that the spin shows up in one place regular, and another place squared, because that's how the term shows up in momentum and energy. So you'll have an equation with at most two real roots, one of which is 1.
@ Sinisa Lazarek
Their whole thing is trying to explain orbital decay without General Relativity. Instead they're using some kind of relativistic Newtonian gravity -- same equation as Newton but the interaction is limited to c so the apparent location of the central body would 'lag' behind it's actual location.
Frankly I'm willing to bet that they messed up the math showing this would cause orbital decay. Intuitively it seems that it would just move the barycenter's effective location.
@CB (#51):
Thanks, I just realized my mistake in #41: I considered the special case of equal masses and equal orbital radius...
@Sinisa Lazarek (#49) & CB (#52):
CB is right: GR predicts the decay of orbits. Also, the idea above predicts the decay of orbits. Certainly, we do not "really" need another method, but for me it is interesting that simply regarding runtime of gravity yields the same result at Keplerian/Newtonian level...
The shortened "runtime-related" distance is like Lorentz contraction, which is the same as increased mass using non-contracted distance. The result: Acceleration of orbital velocity.
The barycenter will actually get an orbit, with opposit current positions for both masses at the same time.
I for one would thrilled to find out old Albert got it wrong at some point, but it ain't the case here. As counter intuitive as it is at the beginning, the more you dwell on spacetime and curves, the more sense it starts to make. Don't mean the math, but logicaly. Once you view spacetime as an entity, it's pretty easy to understand grav. waves. Everything interacts with everything else, and all of that interacts with spacetime. So no "forever" is possible, everything that has energy has mass and thus curves and thus there is grav. friction and something gets radiated away.
@Sinisa Lazarek (#54):
I also think, Albert Einstein is right, but he did not tell us all about his way towards the simple result. Before developing his curved spacetime metric he certainly also regarded runtime of gravity. But you can't calculate with it as easily as with curved spacetime, which quasi prefetches all results seen from the sight of one mass' frame.
But: what if you move several masses within spacetime? Easy to calculate? May be in special cases its easier to use runtime of gravitation together with Kepler/Newton...
Thanks a lot for this nice discussion, also to CB!
SCHWAR_A:
I highly recommend "Relativity: The Special and General Theory" by Albert Einstein. It's pretty accessible for such a topic.
In the section on General Relativity he shows how starting from the basic postulate that the General Principle of Relativity (that the laws of physics have the same formulation in ALL reference frames, including accelerating ones), one must conclude that gravity and other forms of acceleration are indistinguishable.
He then uses a thought experiment very similar to famous train thought experiment from SR, only now one observer is standing on the outside of a rotating ring. Taking into account the observer's centripital acceleration -- which Einstein literally refers to as a "gravitational field" having already explained why he is justified in doing so -- he shows that to maintain a consistent picture of events that the space between him and some other reference frame cannot be Euclidean. The gravitational field must, necessarily from the postulates, mean that the spacetime metric is changed.
It's a great book that really helped illuminate the motivation behind relativity for me.
I don't know that this was the actual progression of his thought when coming up with the idea, but it makes a lot of sense that when trying to extend his Special Theory of Relativity to the general case, he'd start with extending the Special Principle of Relativity that was the foundation of SR to the General Principle and move on from there in much the same way he did for SR.
Anyway, If he did try just adding non-instantaneous gravity, he must have found it didn't work. Certainly one would not expect it by itself to produce all the predictions of GR. And I do believe it doesn't produce any of the same predictions, and your calculation that it results in orbital decay is wrong. The slightly different angle would remain constant making it simply appear as though the central body was also orbiting a slightly different barycenter than you otherwise get, and the acceleration being higher than it would be than in the instantaneous case would only mean that orbital velocity is slightly higher than it would be in the Newton formulation. Not that it would spiral inward.
Finally, your formulation in #41 is wrong in all cases. Yes the energies of two identical objects orbiting each other around a common barycenter would have the same energy. But that's not how Conservation of Energy works. For that you need to know that the SUM of energies is a constant, as in:
E_m + E_M = C where C is some constant.
In your special case, that would just be 2E_m = C, and you'd have to show that it remains true as the orbit changes, along with 2L_m = D also holding true, and that will not happen.
My other motivation for saying your calculation must be wrong is that 1) your result violates Conservation Laws, and 2) light-speed gravity would appear to be rotationally symmetric and translation-ally symmetric (the result is the same regardless of the specific orientation with respect to the rest of the universe, and the specific date and location) which by Noether's Theorem means it should obey both Energy and Angular Momentum Conservation Laws.
Schwar;
Schwar, it seems you've gone from a radical hypothesis that predicts something very surprising (i.e., that orbital decay with no emitted energy is possible) to a radical hypothesis that predicts exactly the same thing as GR. But only for this case - your idea does not have the breadth of application or wide variety of independent predictions that GR does.
In some respects this makes your hypothesis safer, in that it now seems to be not immediately falsifiable (I'll let others discuss possible math problems). But in other respects, it makes your idea much much less valuable, because really the only thing it had going for it from a 'competing hypothesis' perspective was a novel and eyebrow-raising prediction. If its just "I have an alternative to GR...that predicts absolutely nothing different from it," well, physicists see a lot of that. It doesn't generally impress.
eric:
"Schwar, it seems you’ve gone from a radical hypothesis that predicts something very surprising (i.e., that orbital decay with no emitted energy is possible) to a radical hypothesis that predicts exactly the same thing as GR. "
Nope, it's a very different prediction from GR: orbital decay without gravity waves, violating conservation laws.
That their hypothesis *should* obey conservation laws leads me to believe that they simply did the math wrong, and the prediction of orbital decay is not there.
@CB&eric:
My entry to this discussion indeed was the now refuted (thanks to CB) idea of no-GWs.
Then further analysis of this idea lead me to the illustrative parallelings with SR and GR. If the idea is actually in parallel, it cannot predict different things...(thus it may even be useless!)
"...orbital decay..."
Please look at this figure.
A shorter "felt" distance 2r' yields acceleration of m. At the same time its actual barycenter B’ is orbiting B. Because in this way for r>0 the aberration is Δφ>0, m will be attracted a bit more than with Newton alone (Δφ=0). Consequently m spirals into M. Vice versa for M related to m.
"Then further analysis of this idea lead me to the illustrative parallelings with SR and GR. If the idea is actually in parallel, it cannot predict different things…"
What? No. Only when two things are mathematically IDENTICAL are they incapable of predicting different things. Merely being "parallel" in one particular aspect (light speed propagation of gravity) does not ensure this at all.
"m will be attracted a bit more than with Newton alone (Δφ=0). Consequently m spirals into M. "
Simply experiencing more gravity than Netwon's Law would not result in orbital decay. It would instead result in orbital velocity being higher than Newton would predict via F=mrω^2, the equation used to derive ω in the first place. It's like if G was slightly bigger -- so what? It's not like G is fine-tuned for the only value that allows stable orbits.
Your link is broken, but I do believe so is your math. Like I said, I believe it is impossible for your math to be right (did you do math or just draw a diagram?) because your premise is symmetrical but your result does not follow conservation laws. Noether says that's a no-no.
If you're going to try to calculate it again, I recommend ditching the Δ syntax. Using needlessly complicated expressions like (1 - Δr/r) instead of just the ratio f is my guess for part of why your previous calculations of momentum/energy were wrong. And in particular for showing that your idea results in orbital decay, the "aberration" from Newton is irrelevant. Just calculate the result of your idea directly and show that it causes decay.
But keep in mind that doing so means you have almost certainly made a mistake.
Schwar, very gracious answer, thank you. Most of the time, internet posters (occasionally myself included, mea culpa) are profoundly lacking in the ability to take constructive criticism. Thumbs up for doing so.
@ eric (#62):
Thank you for the flowers :-))
@all:
Sorry, the trick with the href="data:image/jpg;base64,..." seems no longer working...
* Do you have an idea how to include an image in an answer here?
* Is there a preview possibility?
@CB (#61):
Thanks for all the hints.
The picture contains a circle around the barycenter B with both masses M and m in opposite positions, and additionally the previous position of M on its way, connected to m with speed of light c, while m is orbiting with speed v. This demonstrates the aberration sin φ = v/c.
It should illustrate the contraction of the radius of m by Δr from r to r'.
"Simply experiencing more gravity than Netwon’s Law would not result in orbital decay."
I think it is not just simply more gravity. It is the rotating barycenter. Mustn't that cause quadrupole radiation, i.e. gravitational waves, causing orbital decay?
"My entry to this discussion indeed was the now refuted (thanks to CB) idea of no-GWs."
Which is intimately linked to the idea of orbital decay occurring in the first place.
The thing you may not appreciate is that Conservation Laws work both ways. Yes you can work backwards from Conservation of Energy/Momentum which is very useful. But you can also work forward from your rules of mechanics and arrive at a result that conserves both quantities. Newton's Laws of Motion and Gravity by their very formulation conserve energy and momentum -- Newton's 3rd Law is essentially another way of stating momentum conservation. The Conservation Laws were not *additions* to Newton's Laws, it was just a new way of looking at Newton's Laws which already had the Conservation Laws built in.
Noether's Theorem was a way of proving that physical laws with certain features, like Newton's Laws, Maxwell's Laws, or General Relativity, would naturally have conserved quantities like energy and momentum.
So in GR, it's not that it predicts orbital decay, and Oh Noes that would violate conservation of energy but Whew there's this gravity wave thing that saves us. It's that the exact same mechanism that causes orbital decay also causes gravity waves, and by the nature of that mechanism the gravity waves' energy exactly matches that lost in the orbit. Not because you work backward from CoE and say that this must be true (though this is often useful to do), but because that's what GR says would happen in the first place.
Your idea has no mechanism for losing energy. It should not predict losing energy. You must have messed up your math somewhere.
" It is the rotating barycenter. Mustn’t that cause quadrupole radiation, i.e. gravitational waves, causing orbital decay?"
” It is the rotating barycenter. Mustn’t that cause quadrupole radiation, i.e. gravitational waves, causing orbital decay?”
No, why would it? In GR, a normal orbit with a fixed barycenter radiates gravity waves. All that you need is non-spherical and non-cylindrically symmetric rotation.
@CB (#65):
"In GR, a normal orbit with a fixed barycenter radiates gravity waves."
... because GR warps the Euclidian space in a way that we can use the virtual mean fixed barycenter as seen from an outside frame. A very clever mathematical trick. It preserves us from regarding aberration and thus runtimes...
(#64):
"Your idea has no mechanism for losing energy. It should not predict losing energy. You must have messed up your math somewhere."
Thanks to your help I'm working on that... (please hold the line ;-))...
Schwar: I'd say it's important to start at the beginning with all this - with electron spin. We can make an electron (and a positron) from light in pair production. The electron has its magnetic moment, and the Einstein–de Haas effect demonstrates that "spin angular momentum is indeed of the same nature as the angular momentum of rotating bodies as conceived in classical mechanics". Then when you annihilate the electron with a positron you get light. So start with a simple electron model consisting of light going round and round, then simplify it further to light going round a square path. Light bends in a gravitational field, so draw the horizontals curving down a little, and your pen doesn't end up where it started. Hence the electron falls down. It acquires kinetic energy, not from some magical source, but from itself, because "the coordinate speed of light varies in a non-inertial reference frame". It's actually the speed of light that is reducing vertically. See the Einstein quotes below. When you stop the electron with say an electromagnetic field, the kinetic energy is radiated away as a photon. That's not to say gravitational waves don't exist, but instead that they're more like photons than people appreciate. So trying to detect gravitational waves with LIGO might be like a Flatlander trying to measure stretch with a rubber ruler.
1911: If we call the velocity of light at the origin of co-ordinates co, then the velocity of light c at a place with the gravitation potential Φ will be given by the relation c = co(1 + Φ/c²).
1912: On the other hand I am of the view that the principle of the constancy of the velocity of light can be maintained only insofar as one restricts oneself to spatio-temporal regions of constant gravitational potential.
1913: I arrived at the result that the velocity of light is not to be regarded as independent of the gravitational potential. Thus the principle of the constancy of the velocity of light is incompatible with the equivalence hypothesis.
1915: the writer of these lines is of the opinion that the theory of relativity is still in need of generalization, in the sense that the principle of the constancy of the velocity of light is to be abandoned.
1916: In the second place our result shows that, according to the general theory of relativity, the law of the constancy of the velocity of light in vacuo, which constitutes one of the two fundamental assumptions in the special theory of relativity and to which we have already frequently referred, cannot claim any unlimited validity. A curvature of rays of light can only take place when the velocity of propagation of light varies with position. Now we might think that as a consequence of this, the special theory of relativity and with it the whole theory of relativity would be laid in the dust. But in reality this is not the case. We can only conclude that the special theory of relativity cannot claim an unlimited domain of validity; its results hold only so long as we are able to disregard the influences of gravitational fields on the phenomena (e.g. of light).
The word "velocity" is a problem in the English translations. The word he used in German was geschwindigkeit which translates to speed, he referred to c, and to one of the two fundamental assumptions. That's the special relativity postulate, which is the constant speed of light. It isn't constant, and Einstein said it. Repeatedly.
@John:
Very interesting, thanks.
Where do you think is the problem translating "Geschwindigkeit" to "velocity" or "speed"? For me both are the same...
Is the "Lichtgeschwindigkeit" actually higer in gravitational fields, or is in c = co(1 + Φ/c²) the potential negative?
INCORRECT.
Merely ascertaining the gravitational potential at a distance from the orbiting body will show you that you will get changes in the potential at that point.
Therefore giving and taking away energy from that object.
Therefore making it move, just like it was a duck on the ocean. Lots of ducks bobbing up and down, with NAFF ALL to do with "warping euclidian space".
It isn't constant in a non-inertial frame.